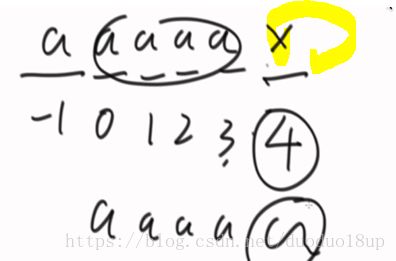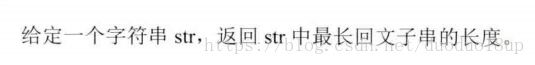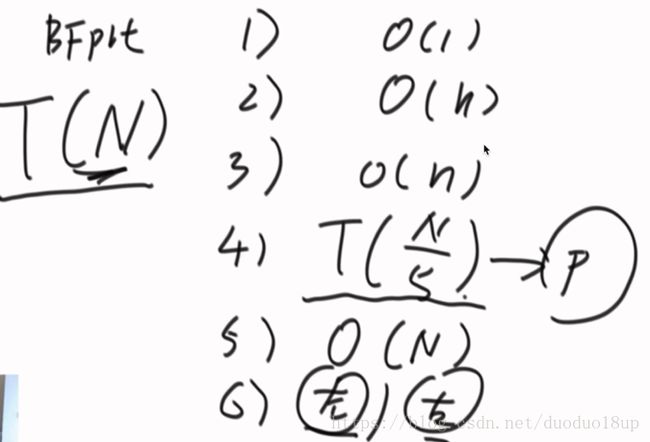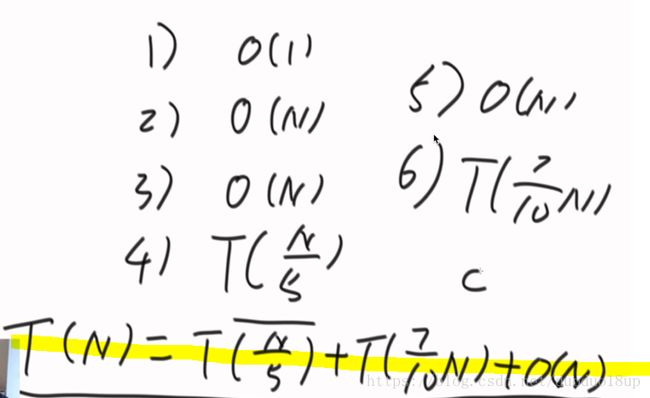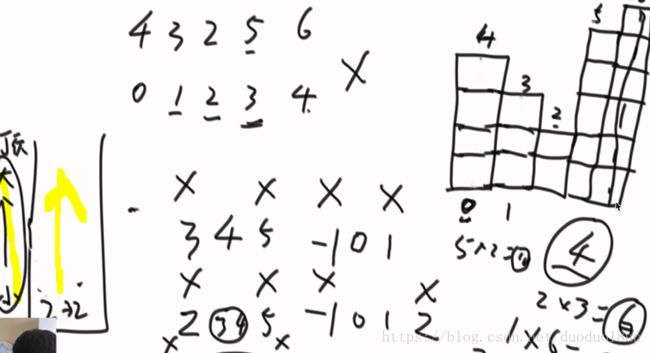左 . 进阶算法---KMP算法

KMP算法：

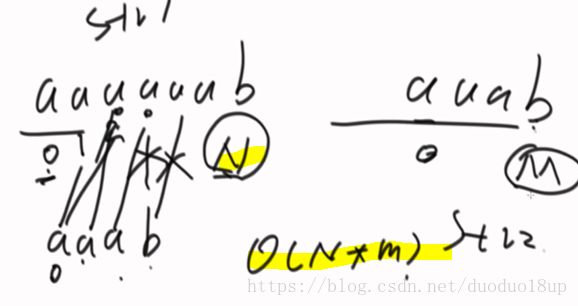
常规想法：

一个个匹配   时间复杂度太高

总结： 我们发现 每次匹配前面的并没有给后面一些指导信息

Note:   子串 和子序列不一样 前者是连续的 后者可以是不连续的   注意区分

详细解释如下：

KMP算法思路:

1  现根据match生成最大前后缀匹配长度数组 ：

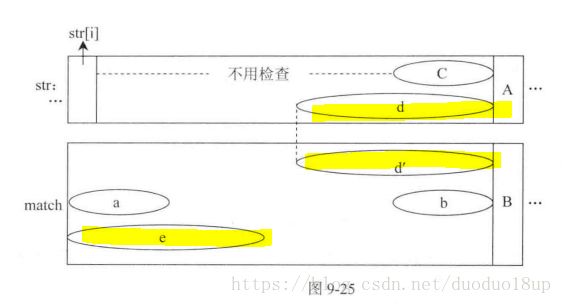
2   从str[i]字符出发---匹配到j位置上发现开始出现不匹配：

3  下一次match 数组往右滑动， 滑动大小为match当前字符的最大前后缀匹配长度，再让str[j]与match[k]进行下一次匹配~

4  注意为什么加快，主要是str[i]--c前那段不用考虑，因为肯定不能匹配~

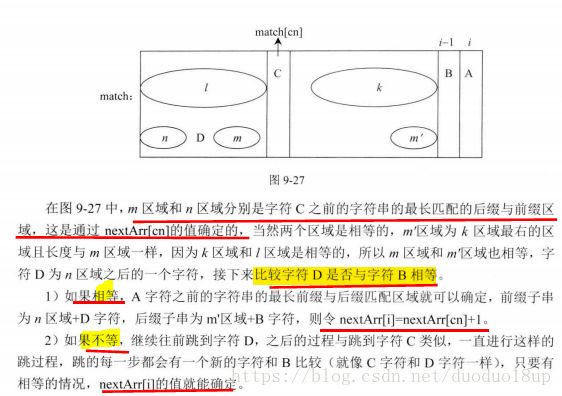
若有匹配 则出现更大的前后缀匹配长度 ，与最初nextArr[] 定义违背。

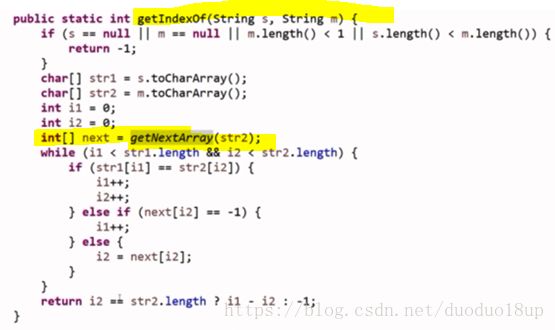
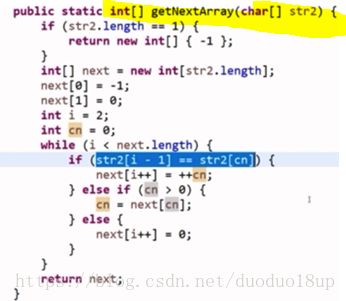
代码： 

关于nextArr数组的求解：

代码：

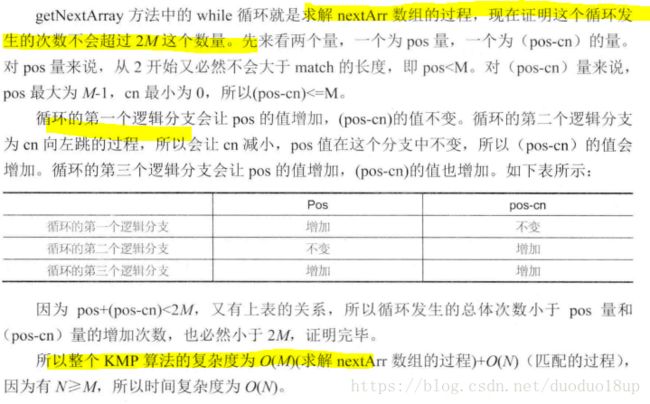
讨论计算复杂度：

相关题目：

1 .给定一个字符串  如何加最短的字符（只能在原始串的后面进行添加）使其构成一个长的字符串且包含两个原始字符串~

思路：其实就是最大前后缀长度数组~   e.g.  abcabc ---->abcabcabc  最少增加3个

多求一位nextArr     可以看出之前4个复用  所以再添一位就好~

总结： 在KMP中nextArr数组基础上 多求一位终止位  将不是的补上即可

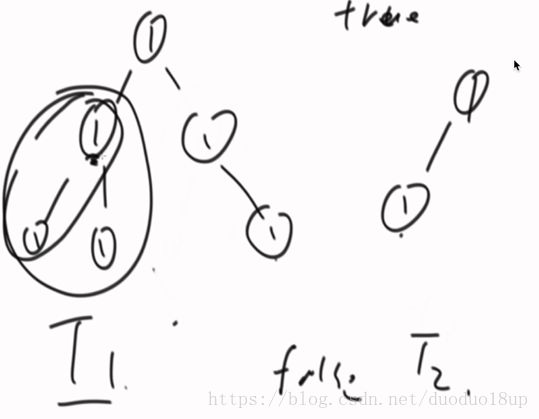
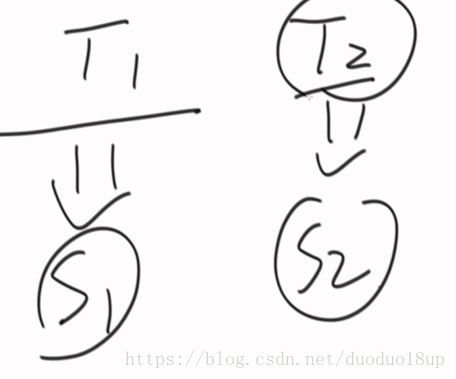
2. 给定两个树  判断树2是否为树1的子树    是则返回true

思路： 把一棵树序列化为字符串（字符数组）   如果str2是str1的子串  则T2也是T1的子树。

3  判断一个大字符串是否由一个小字符串重复得到~

转换为  一个前缀和后缀相差整数倍的问题

Manacher算法（先待定）：

常规思路： 

1    总是从中间那个字符出发--向两边开始扩展--观察回文

      但是奇数位数字完全可以    偶数位数字不可以  会出错

2    经过规律发现 无论是哪种情况  总是  最大值/2  即为最大回文串长度

     前提是 要处理字符串形式  加入特殊字符占位 #进行填充

  这种方法是  暴力法  时间复杂度为O(n2)-----而Manacher算法可以降到O(n)

BFPRT算法：

、

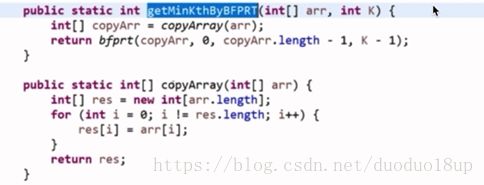
 这个算法其实就是用来解决  ： 求解最小/最大的k个数问题：

 常规的做法 就是 平均时间复杂度为O(n)的 partition函数的应用   ---缺点：是概率式的

 此算法优点是 确定性的。

大概思路：

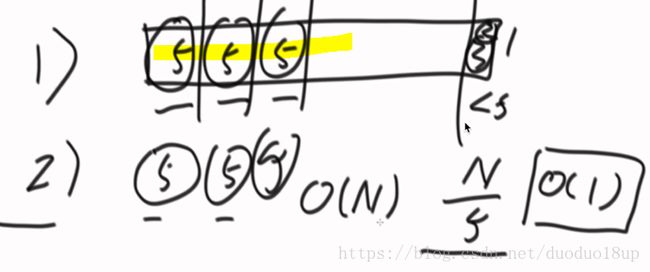
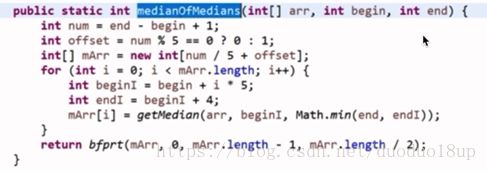
  将整个数组以5个数字一组划分   分别进行组内排序   时间复杂度为O(1)  ---分为N/5组---则总共时间复杂度为O(N)

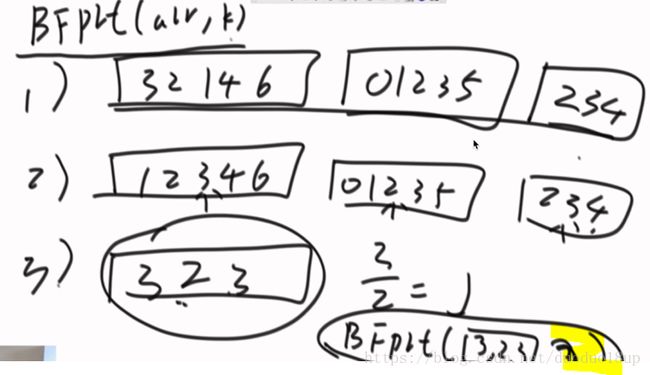
3)  把每个组内的中位数拿出来构成一个新数组   若为偶数 则拿其上中位数即可

4）继续调用 该函数 传入刚才的中位数数组 和  数组长度的一半 （继续求中位数）

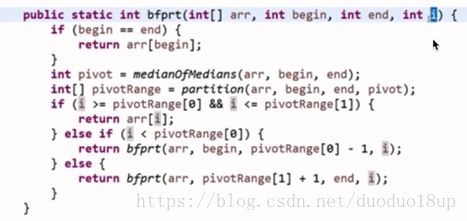
5）将4）返回的值与  k进行对比     左右中 ---

例子：

每一步的时间复杂度为：

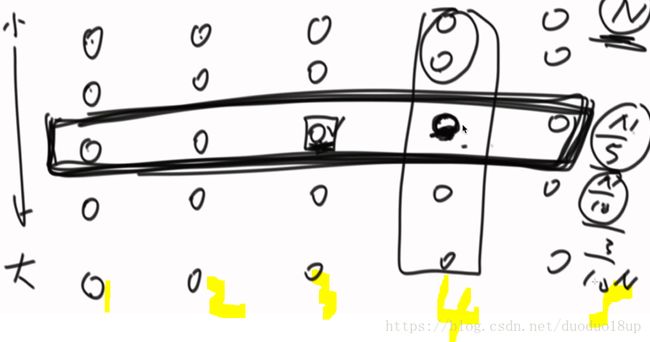
优点 :我们选择的基准一定将数组划分为 一定规模的子部分

由上图我们可以看到： 最中间的中位数--- 右边比它大的至少有N/10 * 3 个（每个组又有两个大于该组中位数的数字）

                                                                右边比它小的最多有N/10 * 7

                                                          ---- 同理左边也是~

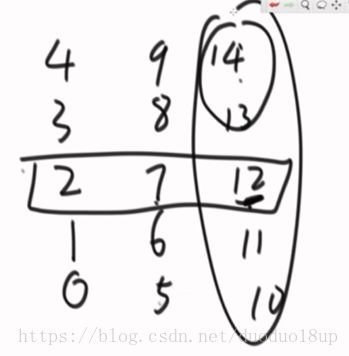
如下例子：   7为中位数  ----比它大的至少有  8 9 12 13 14 这几个数

最终统计时间复杂度为：

重点掌握思路 可以面试的时候告诉面试官~~

代码：

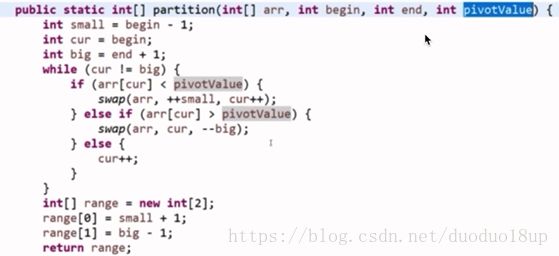
注意： 此时的partition和常规的partition函数不太一样  多了一个我们定义的基准划分值

            且以此基准值划分 比它小的在左边  比它大的在右边 和它相等的在中间并将相等的左右边界存放在一个数组中

窗口：

什么是窗口：

就是一个数组------有L和R指针  当有数字进入时R向右移动    当有数字删除时则L向右移动  且L 和R 不会回退~

思路： 双端队列（链表）

可以从头 尾入  可以从尾  头出

规则：  L< R   且 L,R 永远不回退~

分析逻辑为：  双端队列按照从大到小的顺序  放入元素 

                      （R增加） 头部始终存放的是当前最大的元素---  如果即将进入的元素比上一个进入的元素小 则从尾部进入 连接在后面

                                                                       ------否则   尾部一直弹出（包含相等情况，因为晚过期） 直到为 即将要放入的元素 找到合适的位置

                       （L增加） ---L向右移---（index下标一定得保留）则需要检查当前头部元素index是否过期  若过期则需要从头部进行弹出

具体应用：

生成窗口最大值数组：

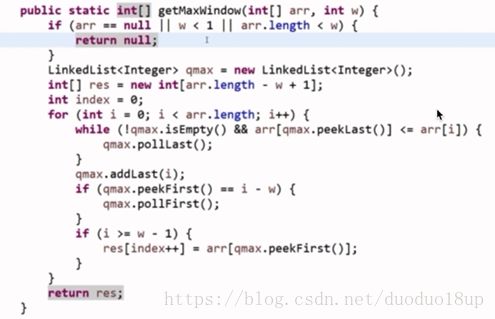
生成窗口最大值数组：

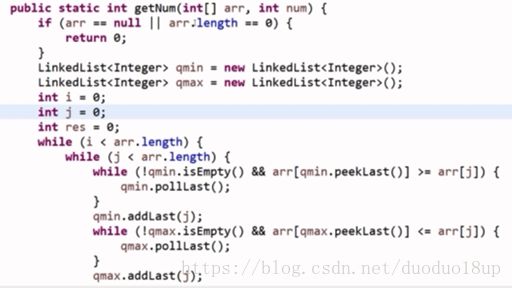
代码：

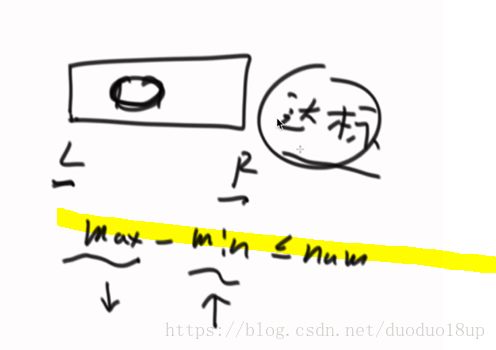
最大值-最小值<=num的子数组数量:

最简单思路： 暴力求解  两个for  依次遍历

分析时间复杂度：  o(N3) n的3次方

最优解思路：

1  如果有一个子数组L-R已经符合要求--则其中内部的子数组一定也符合要求----因为L max--  min++

2  如果已经不达标 则往两边扩也肯定不达标

3 总计规律：  就是L一直往右走 不回退  R也跟着往右扩大范围

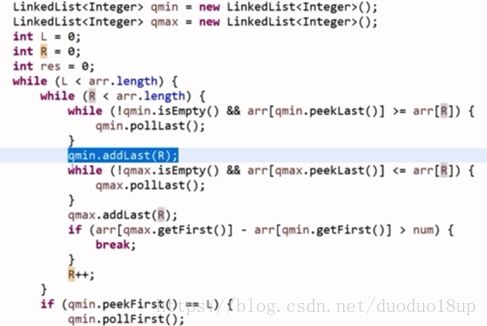
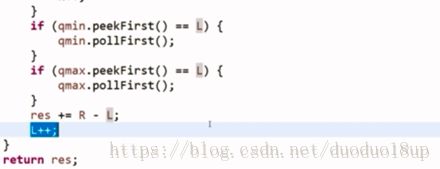
代码：

   

      

单调栈：

问题描述：给定一个数组 请确定每个元素左右距离最近的比它大的数字

常规想法：  到某一个元素时   通过两个for 分别获取其左边比它大的和右边比他大的数字  时间复杂度为O(n2)

最优解思路（单调栈）：

1  一个按照从大到小顺序排序的栈结构    若在压栈过程中发现要压栈的元素和栈顶的元素相比要大  则弹出当前栈顶元素 并从开始弹出处记录   之后继续弹出的下一个即为距离最近的一个元素

注意： 到数组末尾时  但是栈中依然有元素  则此时元素弹出 右为null 而左边为栈中的下一元素

记得 观察 这个元素弹出的驱动是啥？   之前的是因为右边要压栈的比栈顶元素要大  所以可以弹出并记录信息

特殊情况：若出现相等元素情况 则将下标放在一起  等到出现比它们大的数字时再依次弹出即可

具体应用：

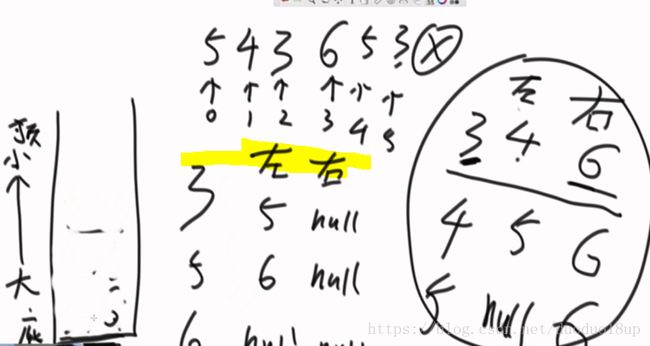
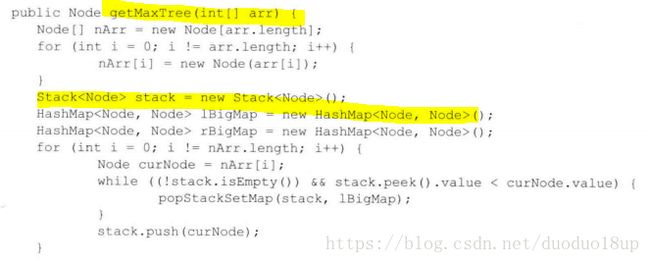
1   构造数组的maxtree:

                 

思路1 ： 按照大根堆思路建立  O(N)

思路2：  单调栈

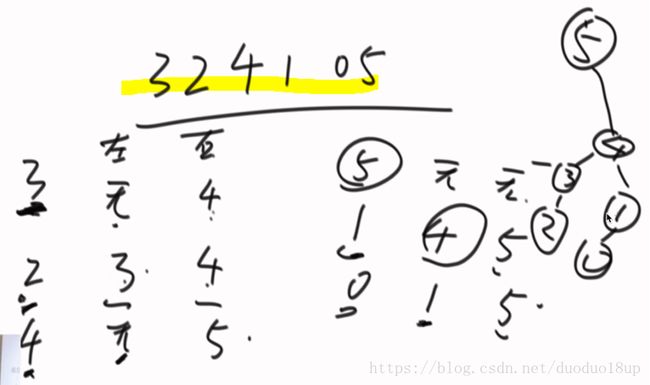
按照单调栈的思路找到每个元素左右最近比它大的元素---分以下几种情况进行讨论：

  1  若一个元素左右均是null 则它是全局最大的  直接作为根节点

  2  若一个元素左或者右 只存在一个  则只具有唯一的父节点

 3   若一个元素左右两个元素均存在 则选择其中最小的那个作为父节点

注意：  一定只能构成一棵树  不会成为多叉树或者森林

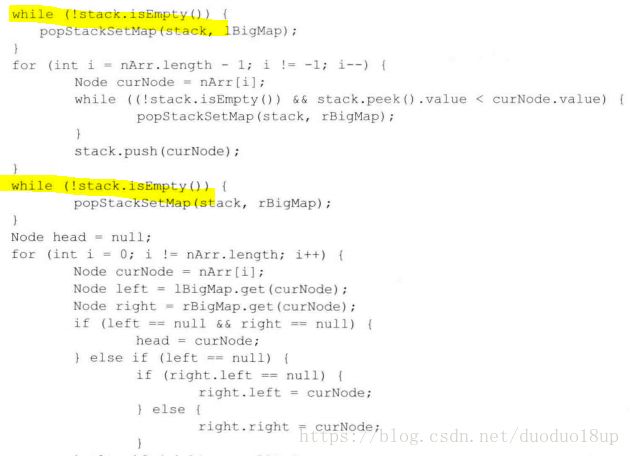
代码：

     

2    求最大子矩阵的大小：

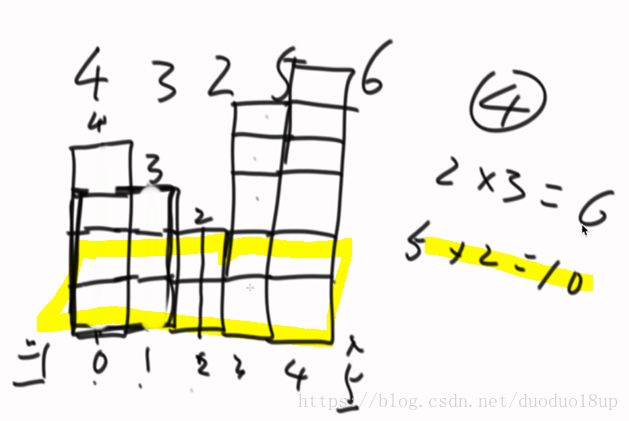
类似的，下图的直方图 ，以每个矩阵的中心高度为杠---然后分别向左右去扩展 ---并记录能够达成的最大格子数目

解法:     用单调栈---从小到大的顺序   若压栈元素<当前栈顶元素  则弹出栈顶元素 

如果栈下面没有元素 则一定能够到达左边界  右边界就是那个压栈元素所在值    

若到最后栈里有元素  但是没有主动让元素弹出的右端元素  则可以最右到达右边界  左边就是下面的元素

转换到原始问题中 ：

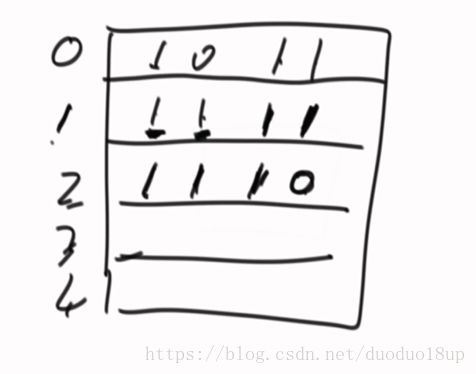
数组为 10 11 

则 对于1 行   2  1 2 2

对于行 3 2 2 0 （注意此时为0 因为最上面是0 并没构成连续的1）

目的就是找到 每一行打底的最大的1的长方形

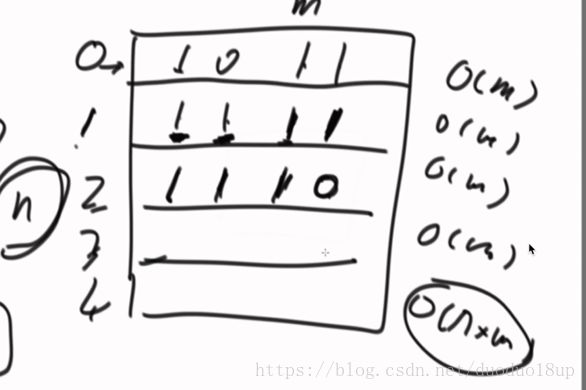
分析时间复杂度： O（n*m ) 就是遍历一遍矩阵

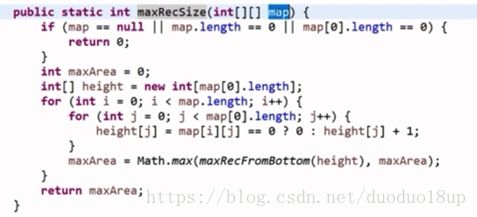
代码：

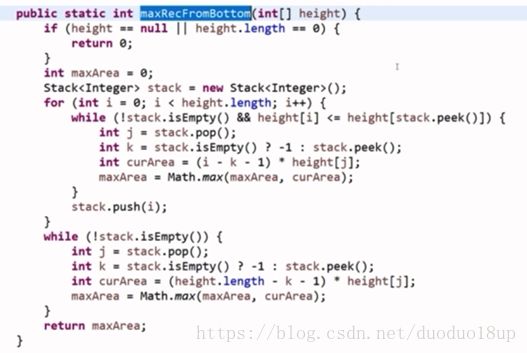
由直方图求解最大矩形：

原问题的主函数：