利用遗传算法求解车辆路径问题
1. 车辆问题描述
车辆路线问题(VRP)最早是由Dantzig和Ramser于1959年首次提出,它是指一定数量的客户,各自有不同数量的货物需求,配送中心向客户提供货物,由一个车队负责分送货物,组织适当的行车路线,目标是使得客户的需求得到满足,并能在一定的约束下,达到诸如路程最短、成本最小、耗费时间最少等目的。
车辆路线问题自1959年提出以来,一直是网络优化问题中最基本的问题之一,由于其应用的广泛性和经济上的重大价值,一直受到国内外学者的广泛关注。车辆路线问题可以描述如下(如图1):

设有一场站(depot),共有M 辆货车,车辆容量为Q,有N位顾客(customer),每位顾客有其需求量D。车辆从场站出发对客户进行配送服务最后返回场站,要求所有顾客都被配送,每位顾客一次配送完成,且不能违反车辆容量的限制,目的是所有车辆路线的总距离最小。车辆路线的实际问题包括配送中心配送、公共汽车路线制定、信件和报纸投递、航空和铁路时间表安排、工业废品收集等。
本程序中对问题进行了优化,选取了中国的34个城市,对他们两两之间的距离都赋上了初始值,出发城市不固定,距离最短即可。最后运行程序可以得到一条最短路径,和经过多少代的选择。
2. 遗传算法介绍
遗传算法(Genetic Algorithm)是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。遗传算法是从代表问题可能潜在的解集的一个种群(population)开始的,而一个种群则由经过基因(gene)编码的一定数目的个体(individual)组成。每个个体实际上是染色体(chromosome)带有特征的实体。染色体作为遗传物质的主要载体,即多个基因的集合,其内部表现(即基因型)是某种基因组合,它决定了个体的形状的外部表现,如黑头发的特征是由染色体中控制这一特征的某种基因组合决定的。因此,在一开始需要实现从表现型到基因型的映射即编码工作。由于仿照基因编码的工作很复杂,我们往往进行简化,如二进制编码,初代种群产生之后,按照适者生存和优胜劣汰的原理,逐代(generation)演化产生出越来越好的近似解,在每一代,根据问题域中个体的适应度(fitness)大小选择(selection)个体,并借助于自然遗传学的遗传算子(genetic operators)进行组合交叉(crossover)和变异(mutation),产生出代表新的解集的种群。这个过程将导致种群像自然进化一样的后生代种群比前代更加适应于环境,末代种群中的最优个体经过解码(decoding),可以作为问题近似最优解。
3. 遗传算法的特点
遗传算法是解决搜索问题的一种通用算法,对于各种通用问题都可以使用。搜索算法的共同特征为:
① 首先组成一组候选解
② 依据某些适应性条件测算这些候选解的适应度
③ 根据适应度保留某些候选解,放弃其他候选解
④ 对保留的候选解进行某些操作,生成新的候选解。
在遗传算法中,上述几个特征以一种特殊的方式组合在一起:基于染色体群的并行搜索,带有猜测性质的选择操作、交换操作和突变操作。这种特殊的组合方式将遗传算法与其它搜索算法区别开来。
遗传算法还具有以下几方面的特点:
(1)遗传算法从问题解的串集开始搜索,而不是从单个解开始。这是遗传算法与传统化算法的极大区别。传统优化算法是从单个初始值迭代求最优解的;容易误入局部最优解。遗传算法从串集开始搜索,覆盖面大,利于全局择优。
(2)遗传算法同时处理群体中的多个个体,即对搜索空间中的多个解进行评估,减少了陷入局部最优解的风险,同时算法本身易于实现并行化。
(3)遗传算法基本上不用搜索空间的知识或其它辅助信息,而仅用适应度函数值来评估个体,在此基础上进行遗传操作。适应度函数不仅不受连续可微的约束,而且其定义域可以任意设定。这一特点使得遗传算法的应用范围大大扩展。
(4)遗传算法不是采用确定性规则,而是采用概率的变迁规则来指导他的搜索方向。
(5)具有自组织、自适应和自学习性。遗传算法利用进化过程获得的信息自行组织搜索时,适应度大的个体具有较高的生存概率,并获得更适应环境的基因结构。
(6)此外,算法本身也可以采用动态自适应技术,在进化过程中自动调整算法控制参数和编码精度,比如使用模糊自适应法。
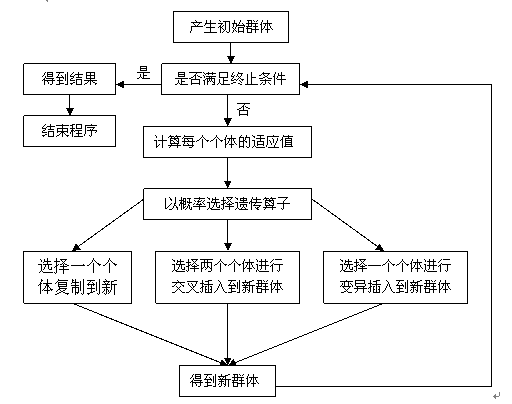
4. 基本流程图
5. 主要功能源码分析
种群的结构体,city数组为单个基因的城市序列,long型的fitness为该基因的适应度,selctp为选择概率(在是否被选择中会用到),exceptp为期望概率,isSelected为判断该基因是否可以进入到下一代。
private class genotype {
int city[] = new int[cityNum];
long fitness;
double selectP;
double exceptp;
int isSelected;
}1.种群初始化
构造函数,初始化种群,将适应度,选择概率,期望概率,是否被选择均置为0,利用随机函数为每个基因分配一个城市序列。最后调用initdistance函数将34个城市之间的距离初始化。
public Yicsf() {
for (int i = 0; i < popSize; i++) {
citys[i] = new genotype();
int[] num = new int[cityNum];
for (int j = 0; j < cityNum; j++)
num[j] = j;
int temp = cityNum;
for (int j = 0; j < cityNum; j++) {
int r = (int) (Math.random() * temp);
citys[i].city[j] = num[r];
num[r] = num[temp - 1];
temp--;
}
citys[i].fitness = 0;
citys[i].selectP = 0;
citys[i].exceptp = 0;
citys[i].isSelected = 0;
}
initDistance();
}2.计算每个种群每个基因个体的适应度,选择概率,期望概率,和是否被选择。
CalAll函数在程序刚开始时执行,初始化适应度,选择概率,期望概率等等条件。然后分别调用CalFitness();CalSelectP();CalExceptP();CalIsSelected();来计算。
public void CalAll(){
for( int i = 0; i< popSize; i++){
citys[i].fitness = 0;
citys[i].selectP = 0;
citys[i].exceptp = 0;
citys[i].isSelected = 0;
}
CalFitness();
CalSelectP();
CalExceptP();
CalIsSelected();
}
计算所有城市序列的适应度,适应度即为一个基因中城市序列的距离的和。最后加上从第一个城市到最后一个城市的距离。
private void CalFitness() {
for (int i = 0; i < popSize; i++) {
for (int j = 0; j < cityNum - 1; j++)
citys[i].fitness += distance[citys[i].city[j]][citys[i].city[j + 1]];
citys[i].fitness += distance[citys[i].city[0]][citys[i].city[cityNum - 1]];
}
}计算选择概率,将所有基因的适应度求和,每个基因的适应度分别除以这个和,即为它的选择概率。
private void CalSelectP(){
long sum = 0;
for( int i = 0; i< popSize; i++)
sum += citys[i].fitness;
for( int i = 0; i< popSize; i++)
citys[i].selectP = (double)citys[i].fitness/sum;
}计算期望概率,即选择概率乘以种群数目。
private void CalExceptP(){
for( int i = 0; i< popSize; i++)
citys[i].exceptp = (double)citys[i].selectP * popSize;
}计算该城市序列是否较优,较优则被选择,进入下一代
private void CalIsSelected(){
int needSelecte = popSize;
for( int i = 0; i< popSize; i++)
if( citys[i].exceptp<1){
citys[i].isSelected++;
needSelecte --;
}
double[] temp = new double[popSize];
for (int i = 0; i < popSize; i++) {
// temp[i] = citys[i].exceptp - (int) citys[i].exceptp;
// temp[i] *= 10;
temp[i] = citys[i].exceptp*10;
}
int j = 0;
while (needSelecte != 0) {
for (int i = 0; i < popSize; i++) {
if ((int) temp[i] == j) {
citys[i].isSelected++;
needSelecte--;
if (needSelecte == 0)
break;
}
}
j++;
}
}3.填充函数
因为初始化是随机的,所以会出现有的基因被多选,有的未被选择,通过填充函数将多选的填充到未选的个体当中。
public void pad(){
int best = 0;
int bad = 0;
while(true){
while(citys[best].isSelected <= 1 && best1)
best ++;
while(citys[bad].isSelected != 0 && bad1)
bad ++;
for(int i = 0; i< cityNum; i++)
citys[bad].city[i] = citys[best].city[i];
citys[best].isSelected --;
citys[bad].isSelected ++;
bad ++;
if(best == popSize ||bad == popSize)
break;
}
} 4 . 交叉函数
交叉函数为executeCrossover, 将个体x和个体y传入该函数,从而产生下一代的城市序列。
private void executeCrossover(int x,int y){
int dimension = 0;
for( int i = 0 ;i < cityNum; i++)
if(citys[x].city[i] != citys[y].city[i]){
dimension ++;
}
int diffItem = 0;
double[] diff = new double[dimension];
for( int i = 0 ;i < cityNum; i++){
if(citys[x].city[i] != citys[y].city[i]){
diff[diffItem] = citys[x].city[i];
citys[x].city[i] = -1;
citys[y].city[i] = -1;
diffItem ++;
}
}
Arrays.sort(diff);
double[] temp = new double[dimension];
temp = gp(x, dimension);
for( int k = 0; k< dimension;k++)
for( int j = 0; j< dimension; j++)
if(temp[j] == k){
double item = temp[k];
temp[k] = temp[j];
temp[j] = item;
item = diff[k];
diff[k] = diff[j];
diff[j] = item;
}
int tempDimension = dimension;
int tempi = 0;
while(tempDimension> 0 ){
if(citys[x].city[tempi] == -1){
citys[x].city[tempi] = (int)diff[dimension - tempDimension];
tempDimension --;
}
tempi ++;
}
Arrays.sort(diff);
temp = gp(y, dimension);
for( int k = 0; k< dimension;k++)
for( int j = 0; j< dimension; j++)
if(temp[j] == k){
double item = temp[k];
temp[k] = temp[j];
temp[j] = item;
item = diff[k];
diff[k] = diff[j];
diff[j] = item;
}
tempDimension = dimension;
tempi = 0;
while(tempDimension> 0 ){
if(citys[y].city[tempi] == -1){
citys[y].city[tempi] = (int)diff[dimension - tempDimension];
tempDimension --;
}
tempi ++;
}
}5.变异
程序开始时,初始化变异概率pmultation为0.05,通过随机函数判断如果小于等于这个概率,则发生变异。随机产生两个城市序号,将这两个城市,调换顺序。
public void mutate(){
double random;
int temp;
int temp1;
int temp2;
for( int i = 0 ; i< popSize; i++){
random = Math.random();
if(random<=pmultation){
temp1 = (int)(Math.random() * (cityNum));
temp2 = (int)(Math.random() * (cityNum));
temp = citys[i].city[temp1];
citys[i].city[temp1] = citys[i].city[temp2];
citys[i].city[temp2] = temp;
}
}
}6.判断是否结束
程序开始时,会定义一个long型的result数组,初始化为所有数字都不相等。在遗传算法进行计算时,result的值会进行变化,直到找到最优解,就会返回true,程序结束。
private boolean isSame(long[] x){
for( int i = 0; i< x.length -1; i++)
if(x[i] !=x[i+1])
return false;
return true;
}7.计算程序执行时间
计算算法所执行的时间
public void CalTime(Calendar a,Calendar b){
long x = b.getTimeInMillis() - a.getTimeInMillis();
long y = x/1000;
x = x - 1000*y;
System.out.println("算法执行时间:"+y+"."+x+" 秒");
}6. 结果分析
经过多次运行,因为初始化的随机,和变异虽然每次迭代的代数不相同,有时需要4000多代,有时甚至需要10000多代。但最优的解均为66,但序列可能会发生变化。
—————– 第 1 代 ————————-
最优的解:286
—————– 第 2 代 ————————-
最优的解:278
—————– 第 3 代 ————————-
最优的解:278
—————– 第 4 代 ————————-
最优的解:278
—————– 第 5 代 ————————-
最优的解:286
—————– 第 6 代 ————————-
最优的解:280
—————– 第 7 代 ————————-
最优的解:280
—————– 第 8 代 ————————-
最优的解:280
—————– 第 9 代 ————————-
最优的解:280
—————– 第 10 代 ————————-
最优的解:270
—————– 第 11 代 ————————-
最优的解:270
—————– 第 12 代 ————————-
最优的解:270
—————– 第 13 代 ————————-
最优的解:270
—————– 第 14 代 ————————-
最优的解:302
—————– 第 15 代 ————————-
最优的解:292
—————– 第 16 代 ————————-
最优的解:292
—————– 第 17 代 ————————-
最优的解:264
—————– 第 18 代 ————————-
最优的解:264
—————– 第 19 代 ————————-
最优的解:284
—————– 第 20 代 ————————-
最优的解:284
—————– 第 21 代 ————————-
最优的解:284
—————– 第 22 代 ————————-
最优的解:276
—————– 第 23 代 ————————-
最优的解:284
—————– 第 24 代 ————————-
最优的解:284
—————– 第 25 代 ————————-
最优的解:284
—————– 第 26 代 ————————-
最优的解:284
—————– 第 27 代 ————————-
…………………………………………….
—————– 第 8630 代 ————————-
最优的解:66
—————– 第 8631 代 ————————-
最优的解:66
—————– 第 8632 代 ————————-
最优的解:66
—————– 第 8633 代 ————————-
最优的解:66
—————– 第 8634 代 ————————-
最优的解:66
—————– 第 8635 代 ————————-
最优的解:66
—————– 第 8636 代 ————————-
最优的解:66
—————– 第 8637 代 ————————-
最优的解:66
—————– 第 8638 代 ————————-
最优的解:66
最佳路径的序列:
南京 杭州 长沙 台北 海口 南宁 昆明 拉萨 香港 澳门 广州 福建 贵州 成都 武汉 南昌 长春 北京 上海 天津 重庆 哈尔滨 沈阳 呼和浩特 石家庄 太原 济南 郑州 西安 兰州 银川 西宁 乌鲁木齐 合肥
算法执行时间:0.460 秒
7. 心得体会
通过这次用遗传算法解决车辆路径问题,使我的动手能力大大的加强。也发现了我以前很多学习上的问题。只掌握了表面的原理,一开始编程发现还有很多的问题。解决问题的过程我学到了很多的东西。遗传算法一个重要的函数就是适应度函数,适应度函数值越大,解的质量越好。适应度函数是遗传算法进化过程的驱动力,也是进行自然选择的唯一标准,它的设计应结合求解问题本身的要求而定。还有就是遗传算法的终止函数的设计非常的重要,它直接决定了迭代的次数和最优解。
这次的学习使我对遗传算法有了更深的理解,对我以后的学习会提供帮助。
8. 源码
参考了网上的一些代码
package ycsf;
import java.util.*;
public class Yicsf {
private String cityName[]={"北京","上海","天津","重庆","哈尔滨","长春","沈阳","呼和浩特","石家庄","太原","济南","郑州","西安","兰州","银川","西宁","乌鲁木齐","合肥","南京","杭州","长沙","南昌","武汉","成都","贵州","福建","台北","广州","海口","南宁","昆明","拉萨","香港","澳门"};
//private String cityEnd[]=new String[34];
private int cityNum=cityName.length; //城市个数
private int popSize = 50; //种群数量
private int maxgens = 20000; //迭代次数
private double pxover = 0.8; //交叉概率
private double pmultation = 0.05; //变异概率
private long[][] distance = new long[cityNum][cityNum];
private int range = 2000; //用于判断何时停止的数组区间
private class genotype {
int city[] = new int[cityNum]; //单个基因的城市序列
long fitness; //该基因的适应度
double selectP; //选择概率
double exceptp; //期望概率
int isSelected; //是否被选择
}
private genotype[] citys = new genotype[popSize];
/**
* 构造函数,初始化种群
*/
public Yicsf() {
for (int i = 0; i < popSize; i++) {
citys[i] = new genotype();
int[] num = new int[cityNum];
for (int j = 0; j < cityNum; j++)
num[j] = j;
int temp = cityNum;
for (int j = 0; j < cityNum; j++) {
int r = (int) (Math.random() * temp);
citys[i].city[j] = num[r];
num[r] = num[temp - 1];
temp--;
}
citys[i].fitness = 0;
citys[i].selectP = 0;
citys[i].exceptp = 0;
citys[i].isSelected = 0;
}
initDistance();
}
/**
* 计算每个种群每个基因个体的适应度,选择概率,期望概率,和是否被选择。
*/
public void CalAll(){
for( int i = 0; i< popSize; i++){
citys[i].fitness = 0;
citys[i].selectP = 0;
citys[i].exceptp = 0;
citys[i].isSelected = 0;
}
CalFitness();
CalSelectP();
CalExceptP();
CalIsSelected();
}
/**
* 填充,将多选的填充到未选的个体当中
*/
public void pad(){
int best = 0;
int bad = 0;
while(true){
while(citys[best].isSelected <= 1 && best1)
best ++;
while(citys[bad].isSelected != 0 && bad1)
bad ++;
for(int i = 0; i< cityNum; i++)
citys[bad].city[i] = citys[best].city[i];
citys[best].isSelected --;
citys[bad].isSelected ++;
bad ++;
if(best == popSize ||bad == popSize)
break;
}
}
/**
* 交叉主体函数
*/
public void crossover() {
int x;
int y;
int pop = (int)(popSize* pxover /2);
while(pop>0){
x = (int)(Math.random()*popSize);
y = (int)(Math.random()*popSize);
executeCrossover(x,y);//x y 两个体执行交叉
pop--;
}
}
/**
* 执行交叉函数
* @param 个体x
* @param 个体y
* 对个体x和个体y执行佳点集的交叉,从而产生下一代城市序列
*/
private void executeCrossover(int x,int y){
int dimension = 0;
for( int i = 0 ;i < cityNum; i++)
if(citys[x].city[i] != citys[y].city[i]){
dimension ++;
}
int diffItem = 0;
double[] diff = new double[dimension];
for( int i = 0 ;i < cityNum; i++){
if(citys[x].city[i] != citys[y].city[i]){
diff[diffItem] = citys[x].city[i];
citys[x].city[i] = -1;
citys[y].city[i] = -1;
diffItem ++;
}
}
Arrays.sort(diff);
double[] temp = new double[dimension];
temp = gp(x, dimension);
for( int k = 0; k< dimension;k++)
for( int j = 0; j< dimension; j++)
if(temp[j] == k){
double item = temp[k];
temp[k] = temp[j];
temp[j] = item;
item = diff[k];
diff[k] = diff[j];
diff[j] = item;
}
int tempDimension = dimension;
int tempi = 0;
while(tempDimension> 0 ){
if(citys[x].city[tempi] == -1){
citys[x].city[tempi] = (int)diff[dimension - tempDimension];
tempDimension --;
}
tempi ++;
}
Arrays.sort(diff);
temp = gp(y, dimension);
for( int k = 0; k< dimension;k++)
for( int j = 0; j< dimension; j++)
if(temp[j] == k){
double item = temp[k];
temp[k] = temp[j];
temp[j] = item;
item = diff[k];
diff[k] = diff[j];
diff[j] = item;
}
tempDimension = dimension;
tempi = 0;
while(tempDimension> 0 ){
if(citys[y].city[tempi] == -1){
citys[y].city[tempi] = (int)diff[dimension - tempDimension];
tempDimension --;
}
tempi ++;
}
}
/**
* @param individual 个体
* @param dimension 维数
* @return 佳点集 (用于交叉函数的交叉点) 在executeCrossover()函数中使用
*/
private double[] gp(int individual, int dimension){
double[] temp = new double[dimension];
double[] temp1 = new double[dimension];
int p = 2 * dimension + 3;
while(!isSushu(p))
p++;
for( int i = 0; i< dimension; i++){
temp[i] = 2*Math.cos(2*Math.PI*(i+1)/p) * (individual+1);
temp[i] = temp[i] - (int)temp[i];
if( temp [i]< 0)
temp[i] = 1+temp[i];
}
for( int i = 0; i< dimension; i++)
temp1[i] = temp[i];
Arrays.sort(temp1);
//排序
for( int i = 0; i< dimension; i++)
for( int j = 0; j< dimension; j++)
if(temp[j]==temp1[i])
temp[j] = i;
return temp;
}
/**
* 变异
*/
public void mutate(){
double random;
int temp;
int temp1;
int temp2;
for( int i = 0 ; i< popSize; i++){
random = Math.random();
if(random<=pmultation){
temp1 = (int)(Math.random() * (cityNum));
temp2 = (int)(Math.random() * (cityNum));
temp = citys[i].city[temp1];
citys[i].city[temp1] = citys[i].city[temp2];
citys[i].city[temp2] = temp;
}
}
}
/**
* 打印当前代数的所有城市序列,以及其相关的参数
*/
public void print(){}
/**
* 初始化各城市之间的距离
*/
private void initDistance(){
for (int i = 0; i < cityNum; i++) {
for (int j = 0; j < cityNum; j++){
distance[i][j] = Math.abs(i-j);
}
}
}
/**
* 计算所有城市序列的适应度
*/
private void CalFitness() {
for (int i = 0; i < popSize; i++) {
for (int j = 0; j < cityNum - 1; j++)
citys[i].fitness += distance[citys[i].city[j]][citys[i].city[j + 1]];
citys[i].fitness += distance[citys[i].city[0]][citys[i].city[cityNum - 1]];
}
}
/**
* 计算选择概率
*/
private void CalSelectP(){
long sum = 0;
for( int i = 0; i< popSize; i++)
sum += citys[i].fitness;
for( int i = 0; i< popSize; i++)
citys[i].selectP = (double)citys[i].fitness/sum;
}
/**
* 计算期望概率
*/
private void CalExceptP(){
for( int i = 0; i< popSize; i++)
citys[i].exceptp = (double)citys[i].selectP * popSize;
}
/**
* 计算该城市序列是否较优,较优则被选择,进入下一代
*/
private void CalIsSelected(){
int needSelecte = popSize;
for( int i = 0; i< popSize; i++)
if( citys[i].exceptp<1){
citys[i].isSelected++;
needSelecte --;
}
double[] temp = new double[popSize];
for (int i = 0; i < popSize; i++) {
// temp[i] = citys[i].exceptp - (int) citys[i].exceptp;
// temp[i] *= 10;
temp[i] = citys[i].exceptp*10;
}
int j = 0;
while (needSelecte != 0) {
for (int i = 0; i < popSize; i++) {
if ((int) temp[i] == j) {
citys[i].isSelected++;
needSelecte--;
if (needSelecte == 0)
break;
}
}
j++;
}
}
/**
* @param x
* @return 判断一个数是否是素数的函数
*/
private boolean isSushu( int x){
if(x<2) return false;
for(int i=2;i<=x/2;i++)
if(x%i==0&&x!=2) return false;
return true;
}
/**
* @param x 数组
* @return x数组的值是否全部相等,相等则表示x.length代的最优结果相同,则算法结束
*/
private boolean isSame(long[] x){
for( int i = 0; i< x.length -1; i++)
if(x[i] !=x[i+1])
return false;
return true;
}
/**
* 打印任意代最优的路径序列
*/
private void printBestRoute(){
CalAll();
long temp = citys[0].fitness;
int index = 0;
for (int i = 1; i < popSize; i++) {
if(citys[i].fitness"最佳路径的序列:");
for (int j = 0; j < cityNum; j++)
{
String cityEnd[]={cityName[citys[index].city[j]]};
for(int m=0;m" ");
}
}
//System.out.print(citys[index].city[j] + cityName[citys[index].city[j]] + " ");
//System.out.print(cityName[citys[index].city[j]]);
System.out.println();
}
/**
* 算法执行
*/
public void run(){
long[] result = new long[range];
//result初始化为所有的数字都不相等
for( int i = 0; i< range; i++)
result[i] = i;
int index = 0; //数组中的位置
int num = 1; //第num代
while(maxgens>0){
System.out.println("----------------- 第 "+num+" 代 -------------------------");
CalAll();
print();
pad();
crossover();
mutate();
maxgens --;
long temp = citys[0].fitness;
for ( int i = 1; i< popSize; i++)
if(citys[i].fitness"最优的解:"+temp);
result[index] = temp;
if(isSame(result))
break;
index++;
if(index==range)
index = 0;
num++;
}
printBestRoute();
}
/**
* @param a 开始时间
* @param b 结束时间
*/
public void CalTime(Calendar a,Calendar b){
long x = b.getTimeInMillis() - a.getTimeInMillis();
long y = x/1000;
x = x - 1000*y;
System.out.println("算法执行时间:"+y+"."+x+" 秒");
}
/**
* 程序入口
*/
public static void main(String[] args) {
Calendar a = Calendar.getInstance(); //开始时间
Yicsf tsp = new Yicsf();
tsp.run();
Calendar b = Calendar.getInstance(); //结束时间
tsp.CalTime(a, b);
}
}