基本图论算法--《算法导论》

广度优先搜索（BFS）

算法描述

对于一个给定的图 G(V,E) 和一个源节点 S BFS能遍历所有从 S 出发能到达的节点，并计算 S 能到达每一个节点的距离（最少的边数），并生成一可广度优先搜索树。

代码说明

u.p u 的前驱结点
u.d u 到 S 的距离
u.color u 的状态，WHITE 未被搜索到，GRAY正在被发现，BLACK以搜索结束
Q 队列

伪代码

//初始化每个节点
/*
u.color =WIHTE;
u.p = NIL;
u.d = INF;
s.d = 0;
*/
bfs(G,s)
{
  Queue Q = null;
  Q.enqueue(s);
  while(Q!=null)
  {
    u = Q.dequeue;
    for each v in G.Adj[u]
        if v.color == WIHTE
            v.color = GRAY
            v.d = u.d+1
            v.p = u
            Q.enqueue(v)
    u.color = BLack
  }
}

深度优先搜索（DFS）

伪代码

time 全局变量描述深度优先搜索的时间轴
u.s 刚发现顶点 u 的时间。
u.f 遍历完 u 的时间
s 之前， u 的颜色为白色。 f 之后 u 的颜色为黑色
颜色标记如bfs

DFS(G)
1、FOR each vertex u∈G.V
2、       u.color=WHITE
3、       u.p=NULL
4、time=0
5、FOR each vertex u∈G.V
6、       IF u.color==WHITE
7、             DFS_VISIT(G,u)
DFS_VISIT(G,u)
1、time++
2、u.s=time
3、u.color=GRAY
4、FOR each vertex v ∈G:Adj[u]
5、       IF v.color==WITHE
6、             v.p=u
7、             DFS_VISIT(G,v)
8、u.color=BLACK
9、time++
10、u.f=time
用聚合分析可以很容易的分析出 DFS 的渐进时间复杂度也是 Θ(V+E) ,不过系数应该会比 BFS 稍大。

值得注意的是深度优先算法所生成的“森林”中包含很多信息

深度优先的性质

1、括号化定理

在对图 G 进行的任意深度优先搜索中，对于图中的节点 u,v ,区间 [u.s,u.f] 与区间 [v.s,v.f] 只能有两种情况：

（a），其中一个区间被另外一个区间完全覆盖，即 u.s<v.s<v.f<u.f （ u 是 v 的祖先）或 v.s<u.s<u.f<v.f ,当且仅当， u,v 之间存在祖先关系

（b）两个区间不重叠，两个顶点在深度优先森林中没有祖先与后代的关系。

2、边的分类
树边： 深度优先搜索树中首先被发现的边

后向边(back): 将顶点 v 连接到他的一个祖先的边。（在伪代码第8行加 ELSE IF v.color==GRAY , (u,v)为后向边 ）

前向边（forword）: u 链接到深度优先搜索树中的一个后代节点 v ,( u.s<v.s )

跨边(cross)

3
对于无向图的深度优先搜索中，每条边要么是树边要么是后向边。
练习

无向图的连通分量

通过 DFS 可以很容易的求出无向图的连通分量。只需将 DFS 做稍许改动
k 表示连通分量数目， v.cc 表示 v 处于第几号连通分量
伪代码

1、FOR each vertex u∈G.V
2、       u.color=WHITE
3、       u.p=NULL
4、time=0
5、k=0
6、FOR each vertex u∈G.V
7、       IF u.color==WHITE
8、             u.cc=++k
9、             DFS_VISIT(G,u)
DFS_VISIT(G,u)
1、time++
2、u.s=time
3、u.color=GRAY
4、FOR each vertex v ∈G:Adj[u]
5、       IF v.color==WITHE
6、             v.p=u
7、             v.cc=u.cc
8、             DFS_VISIT(G,v)
9、u.color=BLACK
10、time++
11、u.f=time

拓扑排序

拓扑排序定义

算法描述
用 DFS 深搜一下，当一个顶点 v 访问结束的时候将它插入到链表的前边

练习
22.4-2

求一个线性时间的算法，算法输入为一个DAG,及两个节点 s,t ，算法输出为 s 到 t 的简单路径的数目
解：
定义P(x)，表示点s到点x的路径数目，P(s)=1，即s到自身有一条路径，其余的所有路径数目都初始化为0。

路径从s到达点x，则必须到达x的上一层结点，假设以x为终点的上一层结点有n个，即a1,a2,…,an，由加法定律可知P(x)= P(a1) + P(a2) + … + P(an)，这是一个从顶向下的递推过程，有点类似于动态规划。

综上，我们只要获取任意一点的入邻接表(也称逆邻接表)，由图G获取其转置GT，其中保存着任意一点的上一层结点。然后再从顶向下递推，正好利用拓扑排序获得的序列，因为由拓扑排序的定义可以保证结点的顺序关系，因此递推有效。以下的算法步骤：

(1) 由图G获取其转置图GT，以得到所有点的入邻接表

(2) 以点s开始作DFS，得到从点s到达点e的拓扑序列

(3) 以此拓扑序列为顺序，逐个获取P值，最终得到P(e)，即s到e的路径数目

图中实线为tree edge，曲线为forward和cross edge，从p到v的路径数目，递推过程如下：

P(p) = 1

P(o) = P(p) = 1

P(s) = P(p) + P(o)= 2

P(r) = P(o) +P(s) = 3

P(y) = P(r) = 3

P(v) = P(y) +P(o) = 4

22.4-3

各出一个算法来判断给定无向图 G=(V,E) 是否包含一个环路，算法的运行时间应该在 O(V) 的数量级，即与| E |无关。

解

我们都知道对于一个无向图而言，如果它能表示成一棵树，那么它一定没有回路，并且有|E|=|V|-1，如果在这个树上添加一条边，那么就构成了回路，如果在这个树中去掉一个边就成了森林（注意：如果只是限定|E|<|V|-1它不一定是森林，它当中可能存在无向连通子图）。

对于这个题目我们可以用DFS来做，每当访问当前节点的邻接表时，如果存在某个邻接的元素已被标记为访问状态，且这个元素不是当前元素的父节点，那么这个图就是存在回路的。总的时间代价是O(|E|+|V|)，因为E<=|V|-1(如果|E|>|V|-1根据无向图的性质，那么这个无向图一定存在回路)，所以O(|E|+|V|)=O(|V|)

强连通分量（SCC）

Kosaraju的算法
1、用 DFS 计算每一个顶点 u 的 u.f
2、计算图 G 的转置 GT
3、对 GT 调用DFS，不过主循环中以 u.f 递减的次序调用

练习

22.5-3
如果第二次调用DFS用原图，并按 u.f 递增次序调用，则算法会更简单，式说明这种算法并不总是正确。

解
这题要注意与书中定理22.14

设 C 和 C′ 为两个不同的强连通分量，若存在一条边 (u,v),u∈C,v∈C′ ,则有 f(C)>f(C′)

加以区分，定理中的结束时间是整个SCC的结束时间，而一个强连通分量中，可能存在某个顶点的结束时间比 f(C′) 要小 ，如图

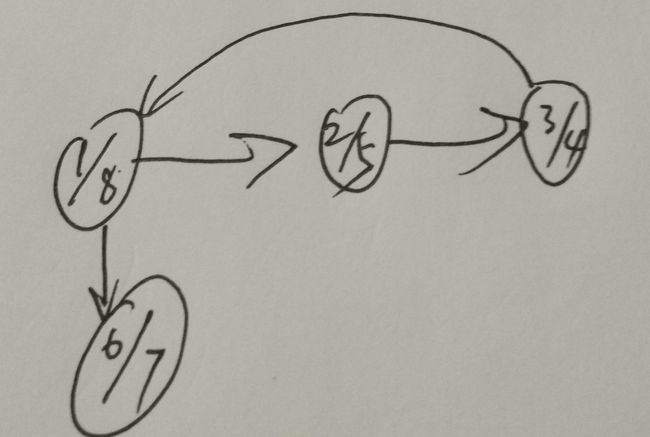
很显然这个算法会把所有节点看成一个连通块