比特币与加密货币技术(Bitcoin and Cryptocurrency Technologies)学习笔记:1.1 密码学中的Hash 函数
本文是 Bitcoin and Cryptocurrency Technologies 第一章 简介与加密货币技术的密码学底层原语(primitive) 的第一小节,主要简介密码学中的hash函数。介绍3个基本性质(与bitcoin相关的), 冲突抵抗(collision-free),隐藏(hiding),puzzle-friendly(PS:不知咋译…)及其简单应用,然后介绍,在BTC中用的多的 SHA-256Hash函数
本文组织如下:
- 通用Hash 函数的3个基本性质
- collision-free 无冲突
- Application: 消息摘要(massage digest)
- Hiding 隐藏性
- Application:数字承诺(commitment)
- puzzle-friendly
- Application: 搜索谜题Search Puzzle
- SHA-256
通用Hash 函数的3个基本性质
- 输入是任意长度的字符串
- 输出是一个固定长度的串,具体的,本书中是256-bits的串
- efficiently computable 计算高效。具体来说,对于一个输入为 n-bit的串计算时间应该是 O(n) O ( n )
比如说我们用在构造hash table中的hash函数就满足这个性质,举个简单的例子是:
H1(x)=x%2256 H 1 ( x ) = x % 2 256
当然在密码学中的hash函数必须要能有足够的密码安全性,因此还需满足如下3个性质(本书仅需如下3个性质):
- collision-free : 无冲突
- hiding: 隐藏
- puzzle-friendly
下面介绍这几个性质
collision-free 无冲突
他的完整定义是这样的:
给定一个hash函数 H(x) H ( x ) , 不可能找到(infeasible to find) x,y,s.t.x≠y,H(x)=H(y) x , y , s . t . x ≠ y , H ( x ) = H ( y )
需要注意的是这里说的是计算上的不可行,不是说没有,因为根据鸽巢原理 (PS:你并不需要知道他是什么),输入的串的个数是远远大于输出的串的个数的,就像你把5个iphone 装入分给3个人,那么总有人会得到两个。
具体来说,如果我们暴力的跑 2256+1 2 256 + 1 次,那么一定会找到 x,y,x≠y,H(x)=H(y) x , y , x ≠ y , H ( x ) = H ( y ) ,更加直觉一点,如果你熟悉生日问题
对于一个来自输入为 n n 种 输出为 m m 种的系统,他们产生碰撞的概念大约是 [参考自维基百科]
也就是说如果 n=2130,N=2256 n = 2 130 , N = 2 256 , 这个值会达到 99% 99 % ,可是计算时间上是不可行的
当然我们这里说的是暴力的计算方法,你或许会想,对于某些hash函数比如说举得第一个例子 H1 H 1 , 肯定可以很简单的找到。然而存在一些hash函数并没有这样直接的方法。密码学中使用的hash函数就满足这个性质。 比较interesting的是,并没有人证明这些在密码学中的hash函数就是 collison-free的,仅仅是对于人来说很难找到,也没有被找到过而已,这并不是说这些函数就是无冲突的。(就像没人找到过上帝,然而你不能说上帝不存在)
Application: 消息摘要(massage digest)
由于无冲突性,那么如果我们得到一对hash值 H(x)=H(y) H ( x ) = H ( y ) ,我们就可以相信, x=y x = y 。举个简单的例子就是 MD5码(已被找到冲突)文件版本检测,试想你在互联网上下载了一个版本,怎样才能保证和下载的是一样的呢,一般他都会在旁边给个MD5码,那你下载下来之后不用去和原版本做对比,仅需对比你的MD5码和原来的MD5码就行了。你需要记忆的量就变小了。
Hiding 隐藏性
这个是说
给定一个hash函数 H H , H H 是隐藏的,如果从一个低信息量(min-entropy,信息论术语,也就是很随机的分布)的分布中找一个秘钥 key k e y , 那么给定 H(key||x) H ( k e y | | x ) , 不可能找到 x x , ‘||’ 符号的意思是链接
简单的来说就是随机的选择这个 key k e y (信息论已证明,等概分布信息熵最大,即最混乱),然后和 x x 链接,计算出 y=H(key||x) y = H ( k e y | | x ) ,不可能找到 x x .
Application:数字承诺(commitment)
下面以一个信封的例子来说明commitment 是什么意思
cmt: 你秘密的选一个值 val v a l , 装到一个信封里,将其密封,然后公布出去
verify:除了你以外没人知道信封里面的消息,而且你不能抵赖,也就是说,你不能欺骗别人,随便说一个消息,因为,打开信封的时候,都能知道里面是什么东西,就能够对你说的进行验证了
然后我们说一下,数字承诺:
可以看到这其实能够与将消息装入信封做出承诺类似的,主要包含两个部分,一个是做出承诺,一个是能验证。具体来说:
H(key||msg),key H ( k e y | | m s g ) , k e y 就相当于公开出去的信封,而msg就是隐藏在信封中的消息,只要自己不公开msg,没人能通过Hash值和key找到msg,但是一旦公布,别人就能验证,而且我们是不可抵赖的,因为由于无冲突性,我们不能找到第二个消息 msg′ m s g ′ 使得 H(key|msg)=H(key|msg′) H ( k e y | m s g ) = H ( k e y | m s g ′ )
puzzle-friendly
如果 hash函数 H H 是puzzle-friendly ,那么,对于任意的 n−bits n − b i t s 的输出 y y , k k 来自于随机分布, H(k||x)=y H ( k | | x ) = y , 我们不能找到一个 x x 在低于 O(2n) O ( 2 n ) 的时间内
也就是说,我们找到x的方法除了暴力搜索整个解空间外,别无它法,或者说,没有比随机选择一个值 x x 更好的解决策略。
Application: 搜索谜题Search Puzzle
搜索谜题是这样描述的:
如果 H H 是puzzle-friendly 的那么不会有比随机选择x更好的策略。这里 |Y| | Y | (这个符号表示集合的元素个数)的大小决定了这个数学游戏的难度。如果 Y Y 包含了所有输出,那你随便找一个 x x 都行,如果, Y Y 仅包含了一个值那么难度最大 O(2n) O ( 2 n ) . 这一性质会在BTC挖矿中用到(bitcoin minning)
SHA-256
这是一个在密码学中用的很广的hash函数,现在还没有找到冲突。这里只简单说一下,不准备深入讲解,sha-2 想深入的可以看看这个Wikipedia。
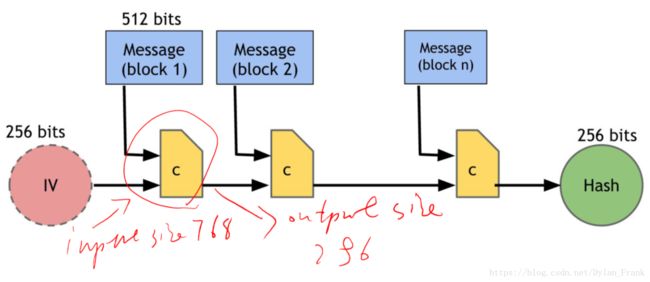
其中的C是一个压缩函数,可以证明如果C是无冲突的那么SHA-256也是无冲突的。他将消息分成 n∗512bits n ∗ 512 b i t s ,每一块都进过C,最终得到hash值