数字图像处理--图像分割
概述
图像处理的两大目的:
- 改善像质(增强,恢复)
- 图像分析:从图像中提取有用的测量数据,对图像内容做出描述,图像识别。
图像分割的基本思路
- 从简到难,主机分割
- 控制背景环境,降低分割难度
- 把焦点放在增强感兴趣的对象,缩小不相干图像成分的干扰上。
图像分割四种不同的方法
- 边缘检测: 检测出边缘,再将边缘像素连接,构成边界形成分割,找出目标物体的轮廓,进行目标的分析、识别、测量等。
- 阈值分割: 最常用法。有直方图门限选择,半阈值选择图像分割,迭代阈值
- 边界方法: 直接确定区域边界,实现分割;有边界跟踪法,轮廓提取法。
- 区域法: 将各像素划归到相应物体或区域的像素聚类方法;有区域增长法等。
阈值分割
基本原理
原始图像—— f ( x , y ) f(x,y) f(x,y)
灰度阈值——T
阈值运算得到二值图像—— g ( x , y ) g(x,y) g(x,y)
g ( x , y ) = { 1 , if f(x,y) ≥ T 0 , if f(x,y) < T g(x,y)= \begin{cases} 1, & \text{if f(x,y) $\geq$ T} \\ 0, & \text{if f(x,y) < T} \end{cases} g(x,y)={1,0,if f(x,y) ≥ Tif f(x,y) < T
阈值的选择包括人工阈值
人工阈值
人工选择法是通过人眼的观察,应用人对图像的知识,在分析图像直方图的基础上,人工选出合适的阔值。也可以在人工选出阈值后,根据分割效果,不断的交互操作,从而选择出最佳的阈值。
直方图阈值的选择
若直方图呈现多个明显的峰值,如三个峰值,取两个峰谷出的灰度值T1,T2作为阈值,同样,可以将阈值化后的图像编程二值化图像。
迭代阈值分割
基本思想:选择一个阈值作为初始值,按某种策略不断地迭代改进,直到满足给定的准则。自动输出一个阈值。在迭代过程中,关键是阈值改进策略,阈值改进策略要求:快速收敛,新产生阈值优于上一次的阈值。
步骤
-
选择图像灰度的中值作为初始阈值 T i = T 0 T_i=T_0 Ti=T0
-
利用阈值把图像分割成两部分区域, R 1 R_1 R1和 R 2 R_2 R2,并计算其灰度均值
u 1 = ∑ i = 0 T i i n i ∑ i = 0 T i n i , u 2 = ∑ i = T i L − 1 i n i ∑ i = T i L − 1 n i u_1=\frac{\sum_{i=0}^{T_i} in_i}{\sum_{i=0}^{T_i} n_i} \quad , \quad u_2=\frac{\sum_{i=T_i}^{L-1} in_i}{\sum_{i=T_i}^{L-1} n_i} u1=∑i=0Tini∑i=0Tiini,u2=∑i=TiL−1ni∑i=TiL−1ini -
计算新的阈值 T i + 1 T_{i+1} Ti+1
T i + 1 = 1 2 ( u 1 + u 2 ) T_{i+1}=\frac{1}{2}(u_1+u_2) Ti+1=21(u1+u2) -
重复步骤2,3直到 T i + 1 T_{i+1} Ti+1和 T i T_{i} Ti的阈值差别小于某个给定值。
这样做的目的就是找到一个T,使得 u 1 = u 2 u1=u2 u1=u2
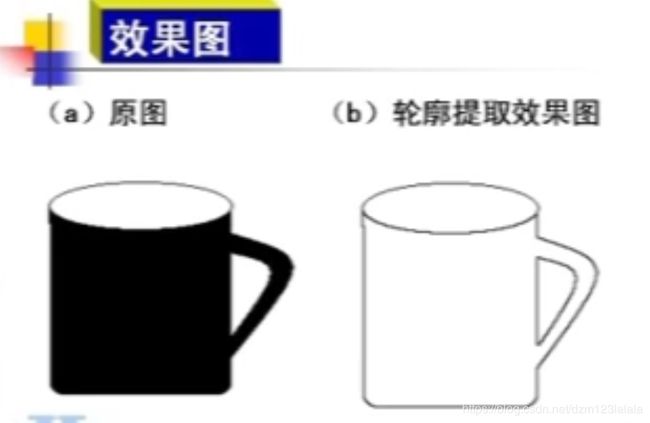
目标物体的轮廓提取
轮廓提取法
图像边缘是图像局部特性不连续性(灰度突变、颜色突变等)的反映,它标志着一个区域的终结和另一个区域的开始。二值图像的轮廓提取采用掏空内部点法:如果原图中有一点为黑,且它的8个相邻点皆为黑,则将该点删除。对于非二值图像,要先进行二值化处理。
边界跟踪法
从图像中一个边界点出发,然后根据某种判别准则搜索下一个边界点,一次搜索出目标边界。
- 确定边界的起始搜索点,起始点的选择很关键,对某些图像,选择不同的起始点会导致不同的结果
- 确定合适边界判别准则和搜索准则,判别准则用于判断一个点是不是边界点,搜索准则则指导如何搜索下个边缘点
- 确定搜索的终止条件。
边界跟踪法一跟踪准则
- 从左下角开始逐点扫描,当遇到边缘点时,则跟踪,直至跟后续点回到起始点(对于闭合线),或其后续点再没有新的后续点(对于非闭合线)为止
- 如果为非闭合线,则跟踪一倒后,需从起始点开始朝相反的方向跟踪到另一尾点。
- 如果不止一个后续点,则按上述连接准则选择距离最近的点为后续点,另一次要的后续点作为新的边缘跟踪起点另行跟踪
- 一条线跟踪完后,接着扫指下一个未跟踪点,直至所有边缘都跟踪完毕
区域增长法
阈值分割法:很少考虑空间关系,使多阈值选择受到限制。
区域分割法:弥补这点不足,利用空间性质,认为属于同一区域的像素应具有相似性。
传统的区域分割算法有:区域增长法和区域分裂合并法。该类方法在先验知识不足的图像进行分割,有较好的性能。但是,空间和时间开销比较大。
区域分裂合并法
利用金字塔或四叉树数据结构的层次概念,将图像划分成一组任意不相交的初始区域即从金字塔或四叉树数据结构的任一中间层开始,根据给定的均匀性检测准则进行分裂和合并这些区域,逐步改善区域划分的性能,直至最后将图像分成数量最少的均匀区域为止。
- 区域分裂
- 形成初始区域
- 对图像的每一个区域 R i R_i Ri,计算 P ( R i ) P(R_i) P(Ri),如果 P ( R i ) = f a l s e P(R_i)=false P(Ri)=false,则沿着某一合适的边界分裂区域。
- 重复步骤2,当没有区域需要分裂时,结束。
- 区域合并
- 区域合并是把相邻的具有相似性的区域合并成一个区域。
- 重要运算:确定两个区域的相似性。
- 评判相似性的方法:基于区域的灰度值,或基于区域边界的强弱性等,简单的方法是比较他们的灰度均值。