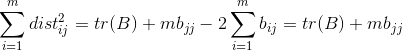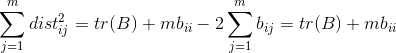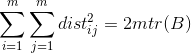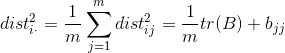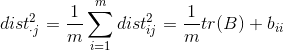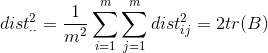流形学习漫谈一：多维缩放(Multiple Dimensional Scaling, MDS)

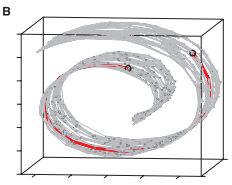
降维算法是机器学习中的重要一部分，通常用的比较多的算法有线性判别分析(LDA)与主成分分析(PCA)等。在此基础上，还有中算法，即流形学习，在计算机视觉中有着广泛的应用。由于直接计算高维特征空间的距离具有很高的错误率(如图所示，高维空间的距离并不合理)，例如，在现实生活中，计算北京到华盛顿之间的距离，如果直接透过地球内部直接计算两点之间直线距离是不合适的，最好的办法是围绕地球表面，在微小的局部上计算直线距离，然后将所有局部距离加起来才更合理。即高维曲面上的两点距离最好的计算方法是通过计算局部空间近邻距离的方式更为合理。

而在流形学习中，常见的算法有Isometric Mapping(即等度量映射)，局部线性嵌入(Locally Linear Embedding)等，其中在介绍Isometric Mapping算法之前，需要先介绍一下多维缩放算法(MDS)，MDS算法与PCA算法均为降维算法的一种。其主要思想是构造低维空间的内积矩阵，使得该内积矩阵中所表达的任意两点之间的距离与高维空间的相应两点距离相等，然后通过对该内积矩阵进行正交特征值分解，析出两个矩阵相乘(即矩阵与矩阵的转置进行相乘)的形式，获得最终的变换矩阵。

现假设有m个样本的高维空间的距离矩阵为，其中表示样本与样本之间的距离。而我们的目标是在低维空间的表示，，同时，还要满足高维空间的对应两个样本点在低维空间之间同样相等，即。

现假设低维空间的内积矩阵为，其中，即表示低维空间两点之间的距离。

接下来的几步西瓜书上的推导其实就是在凑出一种形式，使其满足上面对应的高维空间两点与低维空间两点距离相等的条件。

由于直接衡量距离比较困难，即对于的处理并不容易(就像函数中绝对值问题往往会带来不便求导数的问题一样，一般选择将绝对值转化为平方的方式来求解)。

则此时我们有：

        (1)

(通常，对于样本特征需要进行中心化的预处理，使得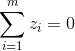，即每个样本特征向量各元素之和为零，则根据低维内积矩阵的构成可以明显看得出，矩阵B的各行与各列之和为0，即)。

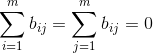那么通过求和可以得到：

 (2)

  (3)

                                              (4)

其中tr(.)表示矩阵的迹，即对角线之和。再令：

                                                      (5)

                                                      (6)

                                                         (7)

以上的操作即构建最原始的平方项之间的相等关系(即公式1的关系)，可以得到：

                                                (8)

即通过该方式可以得到了高维空间内积矩阵与低维空间的内积矩阵的对应关系。

现在已经得到了低维空间的内积矩阵B，因此现在需要对其进行特征值分解，即析出前面所假设的样本在低维空间的表达Z，通过特征值分解可以得到，其中为对角线为特征值的对角矩阵，即，同时特征值是按照从大到小的形式排列，而V的每一列是特征值对应的特征向量。这里需要进行降维的工作了，即舍弃掉一些较小特征值与其对应的特征向量(较小特征值属于噪声的可能性较大)，取的前个特征值，即，而对应的特征向量为。则低维空间的特征表达Z为：

                                                                

关于MDS算法如下描述：

 

MDS算法

输入：距离矩阵D，低维空间数
过程： 1：根据公式5,6,7计算; 2：根据公式8计算矩阵B； 3：对矩阵B进行特征值分解； 4：取为个最大的特征值所构成的对角矩阵，为对应的特征向量矩阵 输出：矩阵，每一行即为低维空间的坐标

 

 

 

 

 

 

 

MDS算法代码：

利用上一篇文章里的MNIST数据集中将0,1数据的特征提取的代码，应用MDS算法，将0,1数据的特征的维度降为二维，进而进行特征可视化。

对于距离矩阵的计算，这里为了能够加快运算速度，只选取前500个样本进行可视化分析。其中关于部分的计算，将其转化为矩阵的计算方式，从而避免逐个元素计算而造成的运算时间长的问题。

的计算相当于计算原始距离矩阵的每个元素的平方，转化为矩阵计算的形式则是相当于将原矩阵的每一行的所有列进行求和然后复制每一列扩充成原始矩阵的大小，则是将原始矩阵的每一列的所有行进行求和，由于原始距离矩阵是对称矩阵，因此所构成的矩阵即将所构成的矩阵转置得到。而所构成的矩阵即将原始距离矩阵所有元素求和，并将其扩充成原矩阵的大小。

则结合上一篇文章的代码如下所示:

'''
This is a function of MDS(Multiple Dimensional Scaling algorithm)
Author: Zongyuan Ding
Reference: Machine Learning (By Zhou Zhihua)
'''
import numpy as np
import matplotlib.pyplot as plt
import logistregression as lg


def mds(distance_matrix, dimension):
    '''
    this function can realize the mds algorithm
    :param distance_matrix: the input samples distance matrix, which d_ij represent the distance of sample i sample j
    :param dimension: the objective dimension to be reduced
    :return: the coordinate of every sample in the low dimensional
    '''
    orignal_dim = distance_matrix.shape[0]
    dis_ij_2 = distance_matrix ** 2

    dis_i_2 = np.sum(distance_matrix, 1)
    dis_i_2 = np.tile(dis_i_2, [orignal_dim, 1])

    dis_j_2 = dis_i_2.T
    dis_2 = np.sum(distance_matrix) * np.ones([orignal_dim, orignal_dim])
    # generate new distance matrix 
    new_distance_matrix = (dis_ij_2 - dis_i_2 - dis_j_2 + dis_2) * (-1 / 2)
    # perform eig value decomposing for the new distance matrix
    eig_value, eig_vector = np.linalg.eig(new_distance_matrix)
    # select the top k big eig values of new distance matrix
    sorted_indices = np.argsort(eig_value)
    took_eig_value = eig_value[sorted_indices[:-dimension - 1:-1]]
    took_vec = eig_vector[:, sorted_indices[:-dimension - 1:-1]]
    gamma = np.diag(np.sqrt(took_eig_value))
    took_vec = np.mat(took_vec)
    gamma = np.mat(gamma)
    coordinate_matrix = took_vec * gamma
    coordinate_matrix = np.array(coordinate_matrix)
    return coordinate_matrix


def main():
    train_f, train_l, test_f, test_l = lg.extract_binary_features()
    dim, num = train_f.shape
    dist_matrix = np.zeros([num, num])
    # calculate the original distance matrix
    for i in range(num):
        for j in range(num):
            dist_matrix[i, j] = np.sqrt(np.sum((train_f[:, i] - train_f[:, j])**2))
    # a = np.array([[1, 2, 3, 4], [2, 3, 4, 5], [3, 4, 5, 6], [4, 5, 6, 7]])
    b = mds(dist_matrix, 2)
    # display the features of 0,1 data reduced the dimension to 2
    for i in range(num):
        if train_l[i] == 1:
            plt.scatter(b[i, 0], b[i, 1], c='red')
        else:
            plt.scatter(b[i, 0], b[i, 1], c='green')
    plt.show()


if __name__ == '__main__':
    main()

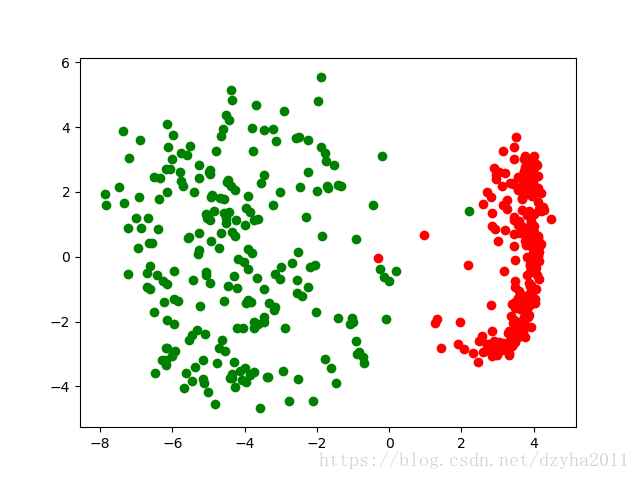
最终通过可视化展示的结果如下图所示（其中红色代表数据1的分布，绿色代表数据0的分布）：

可以看出，通过降维，两类数据被分开的效果很明显，这主要由于降维选取前2个最大的特征值保留了特征的主要分布情况。