深度学习中那些常见的优化算法
先列举一下在深度学习中,我们常见的优化算法有哪些:
- 最基本的如梯度下降(Gradient Descent)—— GD
然后还有一些GD的变体: - 随机梯度下降法(Stochastic Gradient Descent)——SGD
- 小批量梯度下降——mini-batch GD
- 动量梯度下降——Momentum
- 均方根算法(root mean square prop) ——RMSprop
- 自适应矩估计(Adaptive Moment Estimation)——Adam
以上这些之前在吴恩达的课程学过,还有其他的优化算法还没有仔细研究过。
下面这个网站里有都有介绍,有兴趣的可以看看
http://ruder.io/optimizing-gradient-descent/index.html

GD因为是同时处理整个训练集,所以也叫Batch 梯度下降法,GD很简单就不详细介绍了。想看的话我前面博客有介绍。
不过看到有一张图真的是太直观了,所以我贴一下。
GD就是对 cost function J J J 的 “downhill”
SGD:是mini-batch的一个特例,每个mini-batch都只有一个样本
看下Batch GD 和 SGD 在代码上的不同,更有助于理解
- (Batch)GD:
X = data_input
Y = lables
layers_dims = 神经网络的深度(层)矩阵
parameters = initialize_parameters(layers_dims) # 参数初始化
# for loop 迭代 num_iterations 次,更新参数
for i in range(0, num_interations):
predict_lables, caches = forward_propagation(X, parameters) # 前向传播计算预测标签和必要的参数
cost = compute_cost(predict_lables, Y) # 利用预测标签和真实标签求cost function
grads = backward_propagation(predict_lables, caches, parameters) # 后向传播计算梯度值
parameters = update_parameters(parameters, grads) # 更新参数
- SGD
X = data_input
Y = labels
parameters = initialize_parameters(layers_dims)
for i in range(0, num_iterations):
for j in range(0, m):
a, caches = forward_propagation(X[:,j], parameters)
cost = compute_cost(a, Y[:,j])
grads = backward_propagation(a, caches, parameters)
parameters = update_parameters(parameters, grads)
很清晰明了,SGD是对m个样本每一个都要算一次梯度,数量大的时候,速度更快。
但是它是摆动着趋向minimum point,永远不会收敛,会一直在最小值附近摆动。
GD 和 SGD 的运算效果如下图所示

摆动的原理和mini-batch一样,稍后介绍
- Mini-Batch GD
mini-batch 每次更新所用的样本数是介于GD和SGD之间。也就是说mini-batch是把所有样本随机分成很多组,一组一组的计算(SGD就是每组一个样本,Mini-Batch = m)
注意:X、Y的随机分组必须是同步的。
SGD 和 mini-batch 的运算效果如下图所示

摆动的原因:
mini-batch是在得到样本的子集之后就开始更新,但是不同的子集的更新方向都不同,所以cost不会平滑到收敛,而是抖动到收敛。
实现mini-batch的两个步骤:
一:样本随机化(X、Y要同步)
效果如下图所示
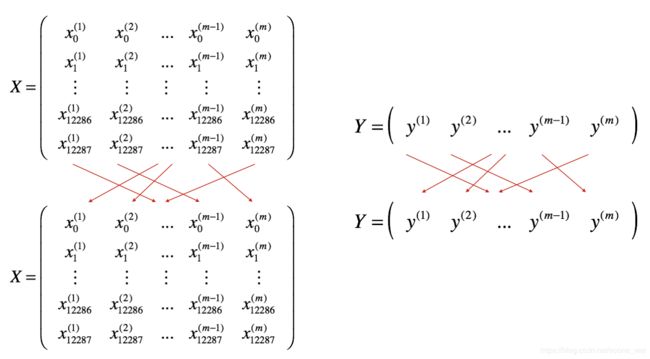
关键代码实现如下:
# 对(X,Y)进行随机改组
permutation = list(np.random.permutation(m))
shuffled_X = X[:, permutation]
shuffled_Y = Y[:, permutation].reshape((1,m))
二:实现分组
假设随机分成64组的话(mini-batch),展示效果如下图所示

(pictures from the deep learning courses of Andrew NG)
关键代码实现:
"""
如果小批量的大小(mini-batch_size)为 64,而总的样本数 m 不是64 的倍数,
那么前 n-1 组中的样本数均为64,最后一组的样本数为 m - 64*(n-1)。(n=m/64向下取整)
"""
num_complete_minibatches = math.floor(m/mini_batch_size) # mini-batch_size = 64 的mini-batch数量
for k in range(0,num_complete_minibatches):
mini_batch_X = shuffled_X[:, k*mini_batch_size:(k+1)*mini_batch_size]
mini_batch_Y = shuffled_Y[:, k*mini_batch_size:(k+1)*mini_batch_size]
mini_batch = (mini_batch_X, mini_batch_Y)
mini_batches.append(mini_batch) # 把n-1组的mini-batch都存放在mini-batches的list中
if m % mini_batch_size != 0:
mini_batch_X = shuffled_X[:, num_complete_minibatches * mini_batch_size:]
mini_batch_Y = shuffled_Y[:, num_complete_minibatches * mini_batch_size:]
mini_batch = (mini_batch_X,mini_batch_Y)
mini_batches.append(mini_batch) # 把最后一组也放到mini-batches的list中
mini-batch 的选择问题:
肯定是在1~m之间选择
如果训练集较小(<2000)的话,直接使用batch梯度下降法就可以
如果训练集比较大的话,一般的mini-batch 大小为64到512(2的整数次方)比较常见。
具体多大,就需要自己尝试了。
.
- Momentum :克服mini-batch的摆动,利用之前的梯度来平滑更新。采用的是指数加权移动平均的方式来实现平滑。
v t = β v t − 1 + ( 1 − β ) θ t v_{t} = \beta v_{t-1} + (1-\beta) \theta_t vt=βvt−1+(1−β)θt简言之,就是给前一个速度施加一定的权重来影响当前的速度。
所以,把指数加权平均的方式应用到Momentum中后,参数更新规则如下:
{ v d W [ l ] = β v d W [ l ] + ( 1 − β ) d W [ l ] W [ l ] = W [ l ] − α v d W [ l ] \begin{cases} v_{dW^{[l]}} = \beta v_{dW^{[l]}} + (1 - \beta) dW^{[l]} \\ W^{[l]} = W^{[l]} - \alpha v_{dW^{[l]}} \end{cases} {vdW[l]=βvdW[l]+(1−β)dW[l]W[l]=W[l]−αvdW[l]
{ v d b [ l ] = β v d b [ l ] + ( 1 − β ) d b [ l ] b [ l ] = b [ l ] − α v d b [ l ] \begin{cases} v_{db^{[l]}} = \beta v_{db^{[l]}} + (1 - \beta) db^{[l]} \\ b^{[l]} = b^{[l]} - \alpha v_{db^{[l]}} \end{cases} {vdb[l]=βvdb[l]+(1−β)db[l]b[l]=b[l]−αvdb[l] w h e r e : β 控 制 指 数 加 权 平 均 数 , α 是 学 习 率 where: \beta 控制指数加权平均数,\alpha 是学习率 where:β控制指数加权平均数,α是学习率
公式所对应的coding如下:
# 用一个 for loop 计算所有的parameters
for l in range(神经网络的层数):
v["dW" + str(l+1)] = beta * v["dW" + str(l+1)] + (1-beta) * grads["dW" + str(l+1)]
v["db" + str(l+1)] = beta * v["db" + str(l+1)] + (1-beta) * grads["db" + str(l+1)]
parameters["W" + str(l+1)] = parameters["W" + str(l+1)] - learning_rate * v["dW" + str(l+1)]
parameters["b" + str(l+1)] = parameters["b" + str(l+1)] - learning_rate * v["db" + str(l+1)]
从以上两公式可以看出,如果参数 β \beta β=0的话,那就是相当于没有Momentum的普通GD了。但是如果 β \beta β=1的话,那就相当于不存在更新了。
虽然Momentum相比前面几种算法,确实可以提高速度了,但是多了一个超参 β \beta β。所以hypeparameters β \beta β 的选择也是一个问题,一般 β \beta β的选择范围是0.8-0.999,默认是0.9。
.
- RMSprop
RMSprop 和 Momentum 很相似,都是为了消除梯度下降中的摆动
参数更新规则如下:
{ S d W = β S d W + ( 1 − β ) d W 2 W = W − α d W S d W \begin{cases} S_{dW} = \beta S_{dW} + (1 - \beta) dW^{2} \\ W = W - \alpha {\frac{dW} {\sqrt{S^{dW}}}} \end{cases} {SdW=βSdW+(1−β)dW2W=W−αSdWdW
{ S d b = β S d b + ( 1 − β ) d b 2 b = b − α d b S d b \begin{cases} S_{db} = \beta S_{db} + (1 - \beta) db^{2} \\ b = b - \alpha {\frac{db} {\sqrt{S^{db}}}} \end{cases} {Sdb=βSdb+(1−β)db2b=b−αSdbdb w h e r e : β 控 制 指 数 加 权 平 均 数 , α 是 学 习 率 where: \beta 控制指数加权平均数,\alpha 是学习率 where:β控制指数加权平均数,α是学习率
所以在知道了Momentum的原理后,RMSprop也不难理解,只是把梯度换成了平方的形式。其中 d W ( d b ) dW(db) dW(db)和 S d W ( S d b ) S_{dW}(S_{db}) SdW(Sdb)变化的方向是一致的,所以在更新的时候除以对应的平方根,可以减缓同方向上的变化,消除摆动。
.
- Adam:结合Momentum和RMSprop两种算法发展出来的一种新算法,被证明是最有效的算法之一。
其更新规则如下:
{ v d W [ l ] = β 1 v d W [ l ] + ( 1 − β 1 ) ∂ J ∂ W [ l ] v d W [ l ] c o r r e c t e d = v d W [ l ] 1 − ( β 1 ) t s d W [ l ] = β 2 s d W [ l ] + ( 1 − β 2 ) ( ∂ J ∂ W [ l ] ) 2 s d W [ l ] c o r r e c t e d = s d W [ l ] 1 − ( β 1 ) t W [ l ] = W [ l ] − α v d W [ l ] c o r r e c t e d s d W [ l ] c o r r e c t e d + ε \begin{cases} v_{dW^{[l]}} = \beta_1 v_{dW^{[l]}} + (1 - \beta_1) \frac{\partial \mathcal{J} }{ \partial W^{[l]} } \\ v^{corrected}_{dW^{[l]}} = \frac{v_{dW^{[l]}}}{1 - (\beta_1)^t} \\ s_{dW^{[l]}} = \beta_2 s_{dW^{[l]}} + (1 - \beta_2) (\frac{\partial \mathcal{J} }{\partial W^{[l]} })^2 \\ s^{corrected}_{dW^{[l]}} = \frac{s_{dW^{[l]}}}{1 - (\beta_1)^t} \\ W^{[l]} = W^{[l]} - \alpha \frac{v^{corrected}_{dW^{[l]}}}{\sqrt{s^{corrected}_{dW^{[l]}}} + \varepsilon} \end{cases} ⎩⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎧vdW[l]=β1vdW[l]+(1−β1)∂W[l]∂JvdW[l]corrected=1−(β1)tvdW[l]sdW[l]=β2sdW[l]+(1−β2)(∂W[l]∂J)2sdW[l]corrected=1−(β1)tsdW[l]W[l]=W[l]−αsdW[l]corrected+εvdW[l]corrected w h e r e : where: where:
– β 1 \beta_{1} β1 和 β 2 \beta_{2} β2 是控制 momentum 和 RMSprop 的 hypeparameters,
– α \alpha α 是学习率
– L 是层数
– ϵ \epsilon ϵ 是避免分母为零所加的一个很小的数
– t 记录了Adam实现的步骤次数
解释一下上面规则的意义:首先计算梯度的指数加权平均值,存储在 v v v中,然后进行偏差矫正,存储在 v d W l c o r r e c t e d v^{corrected}_{{dW^{l}}} vdWlcorrected中。
同理再计算梯度平方的指数加权平均值存存储在 s s s中,然后进行偏差矫正,并存储在 s d W l c o r r e c t e d s^{corrected}_{{dW^{l}}} sdWlcorrected中。
最后用偏差矫正之后的值去更新参数。
更新规则的coding实现:
当然更新之前需要对 v 、 s v、s v、s 初始化
# Perform Adam update on all parameters
for l in range(神经网络层数L):
v["dW" + str(l+1)] = beta1* v["dW" + str(l+1)] + (1-beta1) * grads["dW" + str(l+1)]
v["db" + str(l+1)] = beta1* v["db" + str(l+1)] + (1-beta1) * grads["db" + str(l+1)]
v_corrected["dW" + str(l+1)] = v["dW" + str(l+1)]/ (1-np.power(beta1, t))
v_corrected["db" + str(l+1)] = v["db" + str(l+1)]/ (1-np.power(beta1, t))
s["dW" + str(l+1)] = beta1* s["dW" + str(l+1)] + (1-beta2) * np.power(grads["dW" + str(l+1)], 2)
s["db" + str(l+1)] = beta1* s["db" + str(l+1)] + (1-beta2) * np.power(grads["db" + str(l+1)], 2)
s_corrected["dW" + str(l+1)] = s["dW" + str(l+1)]/ (1-np.power(beta1, t))
s_corrected["db" + str(l+1)] = s["db" + str(l+1)]/ (1-np.power(beta1, t))
parameters["W" + str(l+1)] -= learning_rate * (v_corrected["dW" + str(l+1)] / np.sqrt(s_corrected["dW" + str(l+1)] + epsilon))
parameters["b" + str(l+1)] -= learning_rate * v_corrected["db" + str(l+1)] / (np.sqrt(s_corrected["db" + str(l+1)] + epsilon))
看下Momentum和Adam的cost下降趋势比较
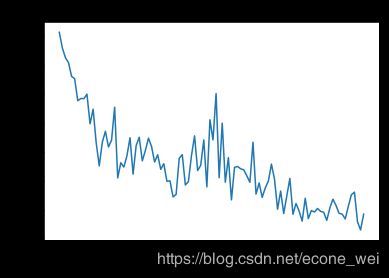
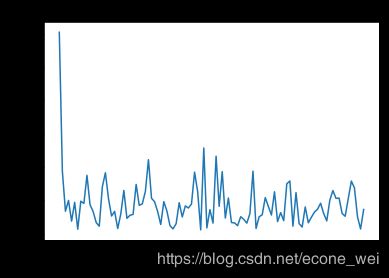
first:cost descent of Momentum
second:cost descent of Adam
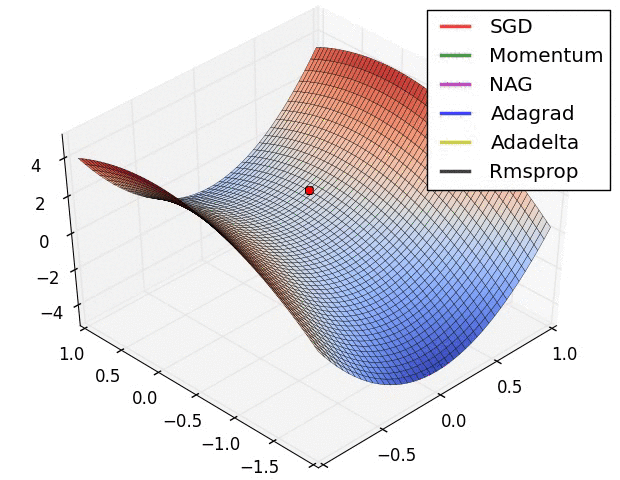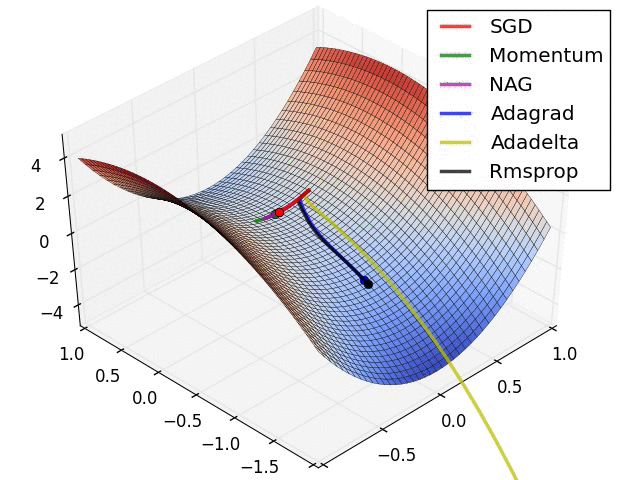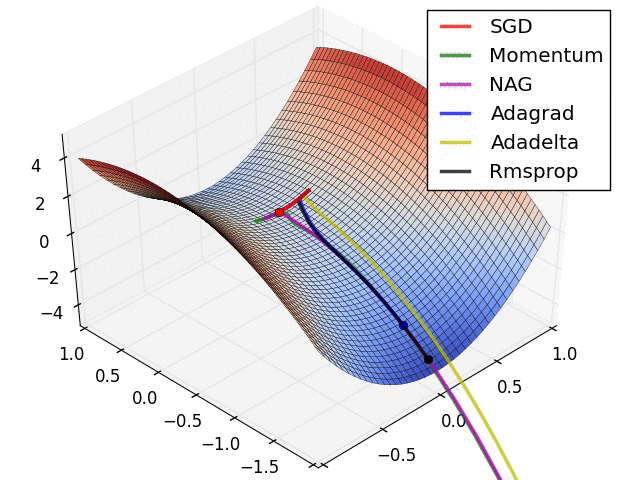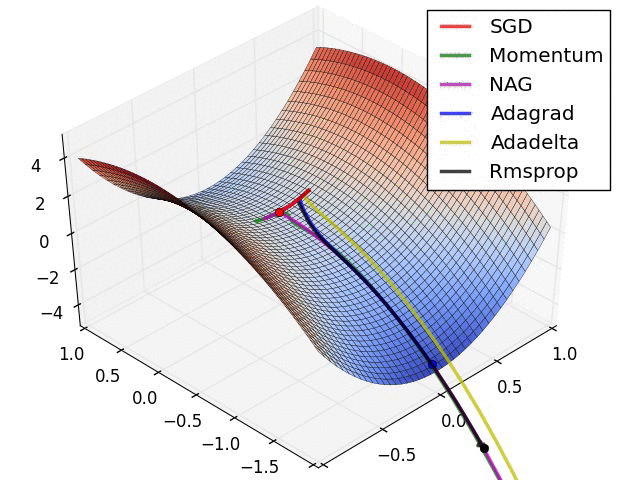
最后引用他人博客里给出的两张GIF图片直观比较一下算法的优化过程
来源地址:https://blog.csdn.net/u010089444/article/details/76725843
另外再贴一下那个详细介绍优化算法的网站,有兴趣的可以看看
http://ruder.io/optimizing-gradient-descent/index.html