计算机视觉（六）：频率域滤波器

一、滤波器

1. 基本滤波公式

      频率域滤波是指先修改一副图像的傅里叶变换，然后计算其反变换，得到处理后的结果。由此，若给定一副大小为 $M\times N$ 的数字图像 $f(x,y)$，则基本滤波公式有如下形式：
$$g(x,y)={\zeta }^{-1}[H(u,v)F(u,v)]$$式中，${\zeta }^{-1}$ 是IDEF，$F(u,v)$ 是输入图像 $f(x,y)$ 的DEF，$H(u,v)$ 是滤波函数（简称为滤波器或滤波传递函数），$g(x,y)$ 是滤波后的输出图像。函数 $F$、$H$ 和 $g$ 是大小与输入图像相同的 $M\times N$ 阵列。

2. 滤波步骤

① 选择滤波器 $H(u,v)$：
      所有的滤波函数 $H(u,v)$ 可理解为大小为 $P\times Q$ 的离散函数，即离散频率变量的范围是 $u=0,1,2,...,P-1$ 和 $v=0,1,2,...,Q-1$。
② 填充 $f(x,y)$：
      通常选择 $P=2M$、$Q=2N$，并对 $f(x,y)$ 添加必要数量的0，形成大小为 $P\times Q$ 的图像。
③ 求 $f(u,v)$ 的DEF $\to F(u,v)$
④ 改变 $F(u,v)$ 的原点至中心：
      换位，将 $F(u,v)$ 的低频部分移到中间，高频部分移到四周，以便后面的计算。
⑤ 计算 $H(u,v)F(u,v)$
⑥ 改变 $H(u,v)F(u,v)$ 的原点至左上角：
      对$H(u,v)F(u,v)$ 的结果进行换位，得到初始时图像的DEF的数据排列形式，即低频部分在四周，高频部分在中间（原点在左上角意味着低频部分在左上角，又因为的DEF是中心对称的，可得初始时图像的DEF应是低频在四周高频在中间）。
⑦ 求 $H(u,v)F(u,v)$ 的IDEF $\to g(x,y)$：
      此时求得的IDEF是一个复数，我们需计算每一个元素的幅度（实部和虚部平方和的平方根），并提取左上角的 $M\times N$ 区域，得到最终的输出图像 $g(x,y)$。

3. 低通滤波器与高通滤波器

      衰减高频而通过低频的滤波器的滤波器称为低通滤波器，将模糊一副图像。
      衰减低频而通过高频的滤波器的滤波器称为高通滤波器，将锐化一副图像。
      一个高通滤波器 $H_{HP}(u,v)$ 和一个低通滤波器 $H_{LP}(u,v)$ 可以有如下关系：
$$H_{HP}(u,v)+H_{LP}(u,v)=1$$也就是说，被低通滤波器衰减的频率能通过高通滤波器，反之亦然。

二、低通滤波器（平滑图像）

1. 理想低通滤波器

      在以原点为圆心、以 $D_0$ 为半径的圆内，无衰减地通过所有频率，而在该圆外“阻断”所有频率的二维低通滤波器，称为理想低通滤波器（ILPE）。它由下面的函数确定：
$$H(u,v)=\{\begin{array}{ll}1,& \text{D(u,v)≤D0}\\ 0,& \text{D(u,v)>D0}\end{array}$$式中，$D_0$ 是一个正常数，$D(u,v)$ 是频率域中点 $(u,v)$ 与频率矩形中心的距离，即
$$D(u,v)=[(u-P/2{)}^2+(v-Q/2{)}^2{]}^{\frac{1}{2}}$$      函数图像如下：

2. 布特沃斯低通滤波器

      截止频率位于距原点 $D_0$ 处的n阶布特沃斯低通滤波器（BLPF）的传递函数定义如下：
$$H(u,v)=\frac{1}{1+[D(u,v)/D_0{]}^{2n}}$$式中，$D(u,v)$ 是距频率矩形中心的距离。与ILPF不同，BLFP传递函数并没有在通过频率和滤除频率之间给出明显截止的急剧不连续性。
      函数图像如下：

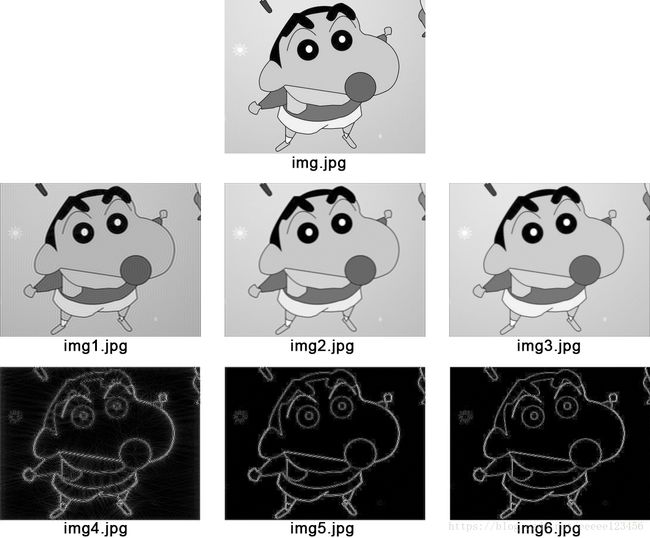
3. 高斯低通滤波器

      二维高斯低通滤波器（GLPF）形式如下：
$$H(u,v)=e^{-D^2(u,v)/2{\sigma }^2}$$式中，$D(u,v)$ 是距频率矩形中心的距离，$\sigma$ 是关于中心的扩展度的度量。
      函数图像如下：

三、高通滤波器（锐化图像）

1. 理想高通滤波器

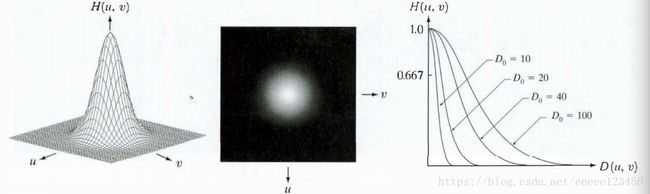
      二维理想高通滤波器（IHPE）定义为：
$$H(u,v)=\{\begin{array}{ll}0,& \text{D(u,v)≤D0}\\ 1,& \text{D(u,v)>D0}\end{array}$$式中，$D_0$ 是截止频率，$D(u,v)$ 是距频率矩形中心的距离。
      函数图像如下：

2. 布特沃斯高通滤波器

      截止频率为 $D_0$ 处的n阶布特沃斯高通滤波器（BHPF）定义为：
$$H(u,v)=\frac{1}{1+[D_0/D(u,v){]}^{2n}}$$式中，$D(u,v)$ 是距频率矩形中心的距离。
      函数图像如下：

3. 高斯高通滤波器

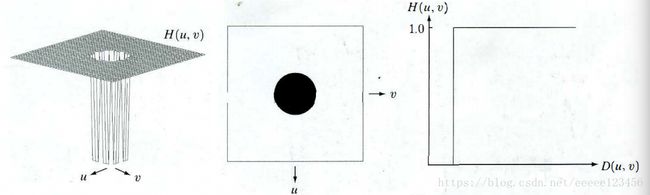
      二维高斯高通滤波器（GHPF）定义为：
$$H(u,v)=1-e^{-D^2(u,v)/2{\sigma }^2}$$式中，$D(u,v)$ 是距频率矩形中心的距离，$\sigma$ 是关于中心的扩展度的度量。
      函数图像如下：

四、代码实现（Python+OpenCV)

cv2.dft()：傅里叶变换
cv2.idft()：傅里叶反变换
cv2.magnitude()：复数转为幅度
cv2.normalize()：标准化图像
numpy.fft.fftshift()：高频移到四周，低频移到中间
numpy.fft.ifftshift()：低频移到四周，高频移到中间

以下代码按照上述的滤波步骤实现：

import cv2
import numpy as np

img = cv2.imread('img.jpg', 0)
rows, cols = img.shape[:2]
d0 = 80

'''
对图像进行傅里叶变换，并返回换位后的频率矩阵
步骤② ：填充输入图像img
步骤③ ：对输入图像进行傅里叶变换得到fft_mat
步骤④ ：对fft_mat进行换位，低频部分移到中间，高频部分移到四周
'''
# 计算最优尺寸
nrows = cv2.getOptimalDFTSize(rows)
ncols = cv2.getOptimalDFTSize(cols)
# 根据新尺寸，建立新变换图像
nimg = np.zeros((nrows, ncols))
nimg[:rows,:cols] = img
# 得到的fft_mat有2个通道，实部和虚部
fft_mat = cv2.dft(np.float32(nimg), flags = cv2.DFT_COMPLEX_OUTPUT)
# 反换位，低频部分移到中间，高频部分移到四周
fft_mat = np.fft.fftshift(fft_mat) 

'''
计算D(u,v)
'''
def fft_distances(m, n):
    u = np.array([i - m/2 for i in range(m)], dtype=np.float32)
    v = np.array([i - n/2 for i in range(n)], dtype=np.float32)
    ret = np.ones((m, n))
    for i in range(m):
        for j in range(n):
            ret[i][j] = np.sqrt(u[i]*u[i] + v[j]*v[j])
    u = np.array([i if i<=m/2 else m-i for i in range(m)], dtype=np.float32)
    v = np.array([i if i<=m/2 else m-i for i in range(m)], dtype=np.float32)
    return ret

'''
步骤① ：选择低通滤波器
'''
def change_filter(flag):
    # 理想低通滤波器
    if flag == 1:
        # 初始化滤波器，因为fft_mat有2个通道，filter_mat也需要2个通道
        filter_mat = np.zeros((nrows, ncols ,2), np.float32) 
        # 将filter_mat中以(ncols/2, nrows/2)为圆心、d0为半径的圆内的值设置为1
        cv2.circle(filter_mat, (np.int(ncols/2), np.int(nrows/2)) , d0, (1,1,1), -1) 
    # 布特沃斯低通滤波
    elif flag == 2:
        n = 2 # 2阶
        filter_mat = None
        duv = fft_distances(*fft_mat.shape[:2])
        filter_mat = 1 / (1+ np.power(duv/d0, 2*n))
        filter_mat = cv2.merge((filter_mat, filter_mat)) # fliter_mat 需要2个通道
    # 高斯低通滤波（σ为d0）
    else:
        filter_mat = None
        duv = fft_distances(*fft_mat.shape[:2])
        filter_mat = np.exp(-(duv*duv) / (2*d0*d0))
        filter_mat = cv2.merge((filter_mat, filter_mat)) # fliter_mat 需要2个通道
    return filter_mat

'''
对图像进行傅里叶反变换，返回反变换图像
步骤⑥ ：对fft_mat进行换位，低频部分移到四周，高频部分移到中间
步骤⑦ ：傅里叶反变换，并计算幅度，提取左上角的 M×N 区域
'''
def ifft(fft_mat):
    # 反换位，低频部分移到四周，高频部分移到中间
    f_ishift_mat = np.fft.ifftshift(fft_mat)
    # 傅里叶反变换
    img_back = cv2.idft(f_ishift_mat)
    # 将复数转换为幅度, sqrt(re^2 + im^2)
    img_back = cv2.magnitude(*cv2.split(img_back))
    # 标准化到0~255之间
    cv2.normalize(img_back, img_back, 0, 255, cv2.NORM_MINMAX) 
    return np.uint8(np.around(img_back))[:rows,:cols]

'''
选择不同的滤波器对图像进行滤波
flag:1理想低通 2布特沃斯低通 3高斯低通
利用 HP+LP=1可计算高频滤波器
对滤波后的结果进行傅里叶反变换，得到输出图像
'''
img1 = ifft(change_filter(1) * fft_mat) # 理想低通
img2 = ifft(change_filter(2) * fft_mat) # 布特沃斯低通
img3 = ifft(change_filter(3) * fft_mat) # 高斯低通
img4 = ifft((1 - change_filter(1)) * fft_mat) # 理想高通
img5 = ifft((1 - change_filter(2)) * fft_mat) # 布特沃斯高通
img6 = ifft((1 - change_filter(3)) * fft_mat) # 高斯高通


cv2.imwrite('img1.jpg', img1)
cv2.imwrite('img2.jpg', img2)
cv2.imwrite('img3.jpg', img3)
cv2.imwrite('img4.jpg', img4)
cv2.imwrite('img5.jpg', img5)
cv2.imwrite('img6.jpg', img6)

以上全部内容参考书籍如下：
冈萨雷斯《数字图像处理（第三版）》