1.3 数值计算

数值计算

通过迭代过程更新解的估计值来解决数学问题的算法，而不是通过解析过程推到出公式来提供正确解的方法。
机器学习中常见的包括优化（找到最大化或者最小化函数的参数）和__线性方程组的求解__。

下溢: 当接近零的数被四舍五入为零时，发生下溢。
上溢：当大量级的数被近似为无穷大时，发生上溢。
解决这种问题的方法之一是使用softmax函数

$softmax(x{)}_i=\frac{exp(x_i)}{\sum exp(x)}$

其实softmax将数值转化为相对概率，数值越大对应的概率越大，这个在分类问题中很常见，是常用的激活函数。

import numpy as np
import tensorflow as tf
array = np.array([-3, 2, -1, 0], dtype=np.float32)
array_soft = tf.nn.softmax(array)
with tf.Session() as sess:
    print(sess.run(array_soft))
    sess.close()

[0.0056533  0.8390245  0.04177257 0.11354961]

病态条件

预留

基于梯度的优化方法

大多数深度学习算法都涉及某种形式的优化，优化是改变x以最小化或者最大化某个函数f(x)的任务。

目标函数（objective function）\代价函数（cost function）\损失函数(loss function)\误差函数(error function)

其实上述是同样的意思，指的要最小化或者最大化的函数

举个例子

梯度下降

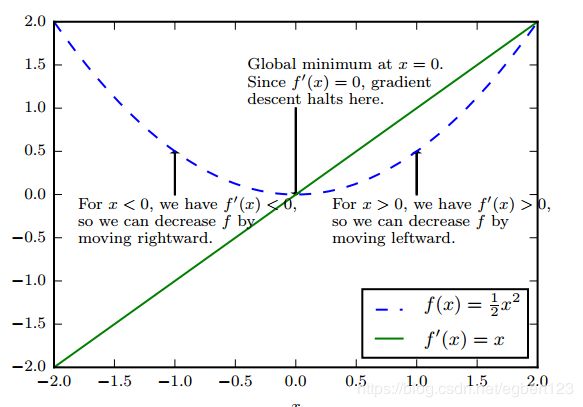
假设我们有函数$y=f(x)$它的导数是$f^{\prime }(x)$，导数代表$f(x)$在点x处的斜率，表明如何缩放输入的小变化才能在输出获得相应的变化$f(x+ϵ)=f(x)+ϵf^{\prime }(x)$

因此导数对于最小化一个函数很有用，它可以指导我们如何改变x来略微的改善y，例如，我们指导对于足够小的$ϵ$来说，$f(x-ϵsign(f^{\prime }(x)))$是比$f(x)$小的，因此可以将x往导数的反方向移动一小步来减少$f(x)$,这种技术成为梯度下降。


针对多维输入的函数，我们需要用到偏导数，偏导数 $\frac{\delta }{\delta x_i}f(x)$衡量点x处只有$x_i$增加时$f(x)$的变化。

梯度是一个相对于一个向量求导的导数：f的导数就是包含所有偏导的向量，${\Delta }_{x}f(x)$。

在$\mu$方向的方向导数就是$f$在$\mu$方向的斜率，也就是$f(x+\alpha \mu )={\mu }^T{\Delta }_{x}f(x)$

为了最小化$f$，希望找到使得$f$下降最快的方向。

$min{\mu }^T{\Delta }_{x}f(x)=min||\mu |{|}_2||{\Delta }_{x}f(x)|{|}_{2}cos\theta$经过简化后，可以得到$mincos\Theta$(其中$\Theta$是$\mu$与梯度的夹角，$||\mu ||=1$), $cos\Theta$在$\Theta =180$获得，也就是$\mu$与梯度的方向相反时取得最小。称为最快梯度下降法。

此时新的点为$x^{\prime }=x-ϵ{\Delta }_{x}f(x)$, 其中$ϵ$称为学习速率，通常选择一个小常数。有时候根据几个$ϵ$计算 $f(x-ϵ{\Delta }_{x}f(x))$并选择其中最小目标函数的$ϵ$，这种策略为在线搜索。

约束优化

有时候，在x的所有可能值下，最大化或最小化一个函数$f(x)$不是我们所希望的，相反，我们可能希望在x的某些集合S中找到$f(x)$的最大值或者最小值。这被称为约束优化。在约束优化术语中，集合S内的点x被称为可行点

KKT方法

广义Lagrangian函数

等式约束，不等式约束

线性最小二乘

首先了解一下什么是最小二乘法

最小二乘法中的二乘其实是平方的意思，最小二乘法也被称为最小平方差

（摘抄）https://blog.csdn.net/quicmous/article/details/51705125

假设手头有三个人的身高/体重调查数据：

编号 身高(cm) 体重(kg)

1 178 80

2 162 55

3 168 53

又假设身高x和体重y关系的数学模型如下：
$y=ax+b$
把调查数据代入上面数学模型得到：

$178a+b=80$

$162a+b=55$

$168a+b=53$

可以写成

$178a+b-80=0$

$162a+b-55=0$

$168a+b-53=0$

合并为一个式子 $(178a+b-80{)}^2+(162a+b-55{)}^2+(168a+b-53{)}^2=0$

虽然让上式左边等于零很困难，但我们想办法让左边的值尽可能小，尽可能接近零。看看参数a,b取何值时，左边取得最小值。然后用这时a,b的值作为方程的近似解总可以吧？于是，求解方程组近似解的问题就变成求下面函数最小值问题了:

$\phi (a,b)=(178a+b-80{)}^2+(162a+b-55{)}^2+(168a+b-53{)}^2$

上面就是最小二乘的基本思路。

通用的我们用$L_2$范数，我们假设我们希望找到最小化下式x值 $f(x)=\frac{1}{2}||Ax-b|{|}_2^2$.

1、首先计算梯度 $\Delta f(x)=A^T(Ax-b)=A^{T}Ax-A^{T}b$

2、将步长$(ϵ)$和容差$(\delta )$设为小的正数

while $||A^{T}Ax-A^{T}b|{|}_2>\delta$ do

$x=x-ϵ(A^{T}x-A^{T}b)$

end while

# 我们例子分析人口与收入的关系
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

def dealData():
    data = pd.read_csv('ex1data1.txt', names=['Population', 'Profit'])
    print(data.head())
    data.insert(0, 'ones', 1)
    cols = data.shape[1]
    X = data.iloc[:, 0:cols-1]
    y = data.iloc[:, cols-1:cols]
    theta = np.zeros((1,2))
    return data, X, y, theta

def computerCost(X, y, theta):
    inner = np.power((np.matmul(X, theta.T) - y), 2)
    return np.sum(inner) / (2 * len(X))

# 更新梯度
def gradientDescent(X, y, theta, alpha, epoch):
    cost = np.zeros(epoch)
    m = X.shape[0]
    for i in range(epoch):
        temp = theta - ((alpha / m) * np.matmul((np.matmul(X, theta.T) - y).T , X))
        theta = temp
        cost[i] = computerCost(X, y, theta)
    return theta, cost

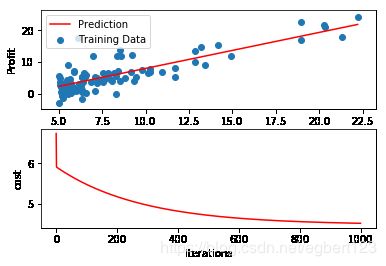
def showLine(data, final_theta, cost):
    plt.subplot(2, 1, 1)
    x = np.linspace(data['Population'].min(), data['Population'].max(), 100)
    f = final_theta[0, 0] + final_theta[0, 1] * x
    plt.plot(x, f, c='r', label='Prediction')
    plt.scatter(data['Population'], data['Profit'], label='Training Data')
    plt.legend(loc=2)
    plt.xlabel('Population')
    plt.ylabel('Profit')

    plt.subplot(2, 1, 2)
    plt.plot(np.arange(1000), cost, 'r')
    plt.xlabel('Iterations')
    plt.ylabel('cost')

    plt.show()


if __name__ == '__main__':
    data , X, y ,theta = dealData()
    final_theta ,cost = gradientDescent(X, y, theta, 0.01, 1000)
    showLine(data, final_theta, cost)

   Population   Profit
0      6.1101  17.5920
1      5.5277   9.1302
2      8.5186  13.6620
3      7.0032  11.8540
4      5.8598   6.8233