7.21 NOIP 2017

NOIP 2017 DAY 1

T1 铺设道路

2013原题，求每个高度差值再前缀和就行。

#include
using namespace std;
int a[10000001],ans,n;
int main(){
	//freopen("road.in","r",stdin);
	//freopen("road.out","w",stdout);
	cin>>n;
	for(int i=1;i<=n;i++){
		scanf("%d",&a[i]); 
	}
	ans+=a[1];
	for(int i=2;i<=n;i++){
		if(a[i]>a[i-1]){
			ans+=a[i]-a[i-1];
		}
	}
	cout<

T2 货币系统

分析题意可知，其实就是求A集合中存在多少个能被其它数组成的数计算出来就行了，我们可以首先对数组排个序，然后对于每一个数考虑能不能被它前面的数字所组成（考试的时候完全背包打错了，结果只得了部分分）。

#include
using namespace std;
int n,ans,a[1000100],t,k;
int f[100001];
int main(){
	//freopen("money.in","r",stdin);
	//freopen("money.out","w",stdout);
	cin>>t;
	while(t--){
		memset(f,0,sizeof(f));
		cin>>n;
		ans=n;
		for(int i=1;i<=n;++i){
			scanf("%d",&a[i]);
		}
		sort(a+1,a+1+n);
		f[0]=1;
		for(int i=1;i<=n;++i){
			if(f[a[i]]){
				ans--;
				continue;
			}
			for(int j=a[i];j<=a[n];j++){
				f[j]=f[j]|f[j-a[i]];
			}
		
	}
	cout<

T3 赛道修建

DAY 2

T1 旅行


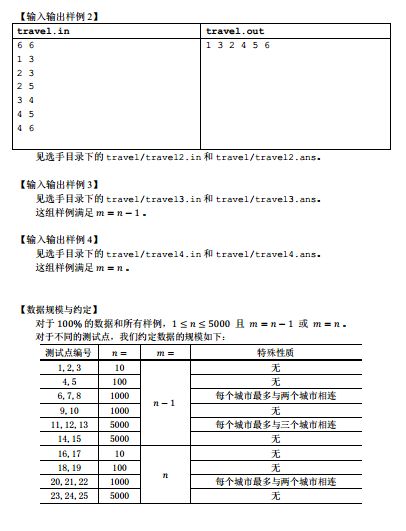
感觉这种难度的题放在第一题也太。。还好我复习了一部分图论，其实想的话也不是特别难，只是比较难实现，就是因为他是无向图，按题目描述有一次往回走的机会，所以可以走过一条边后直接删掉，然后用一个邻接表存编号，然后搜索，最后遍历一下就行。

//orz
#include
using namespace std;
int a[10010],ans[10010],head[10010],vis[10010];
int n,m,dep,x,y,u,v,tot;
vectorver[10010];
struct node{
    int u,v,next;
}edge[10005];
void add(int x,int y){
    edge[tot].u=x;
    edge[tot].v=y;
    edge[tot].next=head[x];
    head[x]=tot++;
}
void dfs1(int Now,int Last){
    if(vis[Now]) return;
    vis[Now]=1;
    a[++dep]=Now;
    for(int i=0;ians[i])
        	return false;
        else return true;
    }
}
int main(){
	//freopen("travel.in","r",stdin);
//	freopen("travel.out","w",stdout);
    cin>>n>>m;
	memset(head,-1,sizeof(head));
    for(int i=1;i<=m;++i){
    	scanf("%d%d",&u,&v);
		add(u,v);
	    add(v,u);
        ver[u].push_back(v);
        ver[v].push_back(u);
    }
    for(int i=1;i<=n;++i)
    	sort(ver[i].begin(),ver[i].end());
    if(n!=m){
    	dfs2(1,-1);
    	for(int i=1;i

T2 填数游戏


这道题通过分析数据可以发现，有65分的数据都是<=3的，很明显可以有两个思路，打表、找规律，然后看题目，虽然题目很长很恶心但是还是不难理解，也就是每个格子右边的格子先往下再往右的路径小于等于下面的格子先往右再往下的路径，通过这个我们就可以先打一个O（2^nm）的暴力搜索，然后配合手推找一下规律。很容易推出当n=1时，答案为2^m，当n=2时，答案为4×3^m-1，而n=3时，手推似乎只能推到3×4,然后我们就用打表分析一下，也能很简单看出规律为112×3^m-2，至于当n>3时，规律性不强而且爆搜（没优化最多n*m<=50）能力不够，也就不好找规律了。
爆搜代码

#include
using namespace std;
const int N=100;
int n,m,a[N][N],ans;
bool check(int x,int y){
    int rx=x,ry=y+1,dx=x+1,dy=y;
    while (rx+ry<=n+m){
        if (a[rx][ry]!=a[dx][dy]){
            return a[rx][ry]n+m){
        for (int i=1;i=1;--i){ //将左下填成1
        if (sum-i>=1 && sum-i<=m)
        {
            a[i][sum-i]=1;
            dfs(sum+1);
        }
    }
    for (int i=n;i>=1;--i){ //回溯时复原
        if (sum-i>=1 && sum-i<=m)
        {
            a[i][sum-i]=0;
        }
    }
}

int main()
{
    cin>>n>>m;
    dfs(2);
    cout<

T3 保卫王国

大概思路应该是状压dp之类的，具体实现。。。
DAY 2完全不是人做的（rp++），over