2019年学期第十一周作业
| 这个作业属于哪个课程 | C语言程序设计II |
|---|---|
| 这个作业要求在哪里 | https://edu.cnblogs.com/campus/zswxy/software-engineering-class2-2018/homework/3201 |
| 我在这个课程的目标是 | 知道递归函数,学汉诺塔问题 |
| 这个作业在哪个具体方面帮助我实现目标 | 题目汉诺塔问题的运用 |
| 参考文献 | c语言程序设计 |
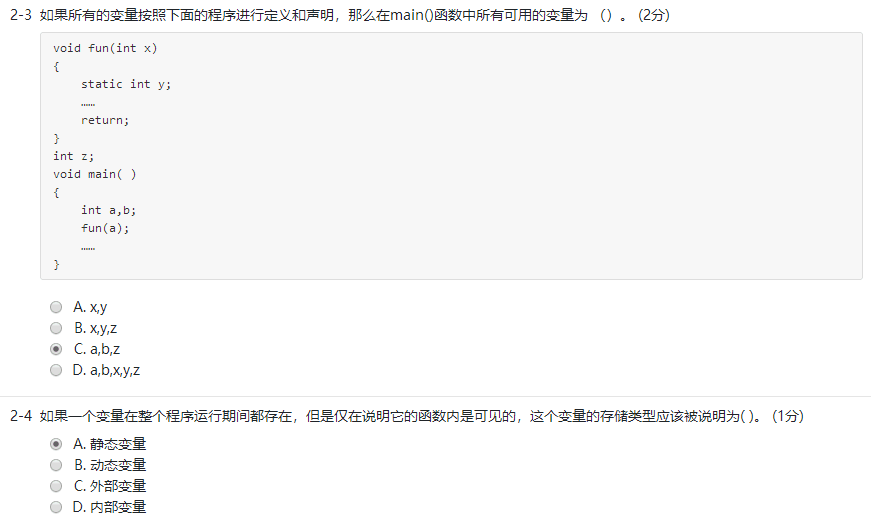
函数题
7-1 汉诺塔问题* (10 分)
汉诺塔是一个源于印度古老传说的益智玩具。据说大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘,大梵天命令僧侣把圆盘移到另一根柱子上,并且规定:在小圆盘上不能放大圆盘,每次只能移动一个圆盘。当所有圆盘都移到另一根柱子上时,世界就会毁灭。
题图1.jpg
请编写程序,输入汉诺塔圆片的数量,输出移动汉诺塔的步骤。
输入格式
圆盘数 起始柱 目的柱 过度柱
输出格式
移动汉诺塔的步骤
每行显示一步操作,具体格式为:
盘片号: 起始柱 -> 目的柱
其中盘片号从 1 开始由小到大顺序编号。
输入样例
3
a c b
输出样例
1: a -> c
2: a -> b
1: c -> b
3: a -> c
1: b -> a
2: b -> c
1: a -> c
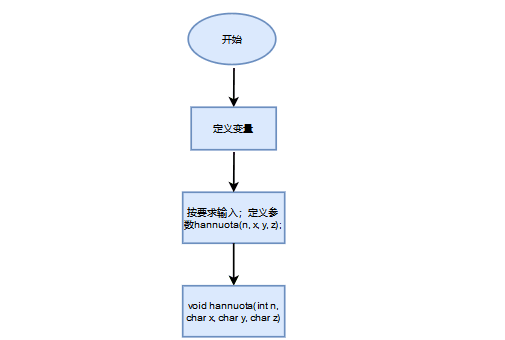
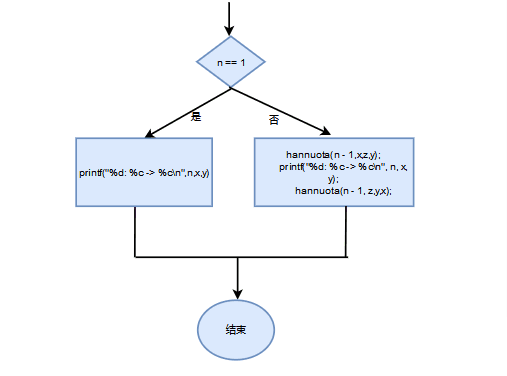
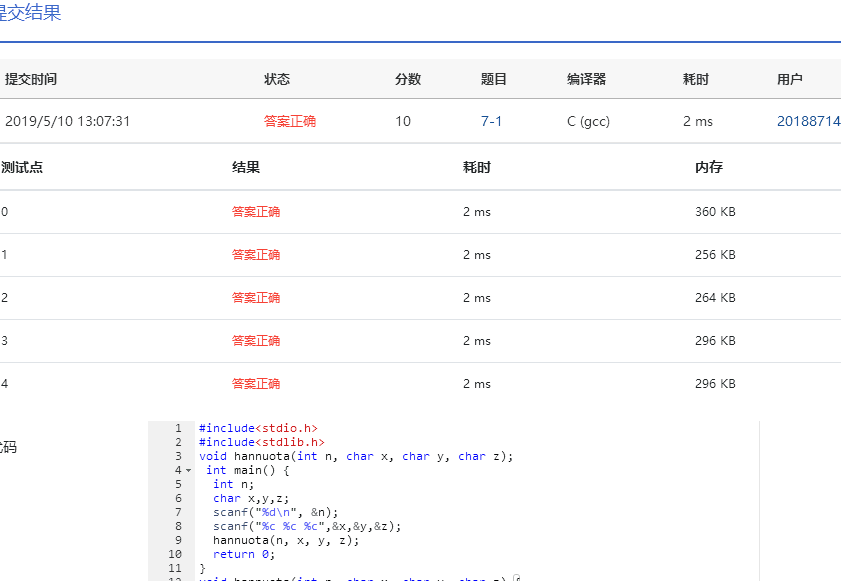
实验代码
#include
#include void hannuota(int n, char x, char y, char z); int main() { int n; char x,y,z; scanf("%d\n", &n); scanf("%c %c %c",&x,&y,&z); hannuota(n, x, y, z); return 0; } void hannuota(int n, char x, char y, char z) { if(n == 1){ printf("%d: %c -> %c\n",n,x,y); } else { hannuota(n - 1,x,z,y); printf("%d: %c -> %c\n", n, x, y); hannuota(n - 1, z,y,x); } } 设计思路
遇到的问题及解决方法
问题:一开始不清楚汉诺塔问题是什么规律,
解决方法:搭档画图给我详细分析了,总之这个题目就是在搭档的帮助下完成的。
正确截图
7-2 估值一亿的AI核心代码 (20 分)
AI.jpg
以上图片来自新浪微博。
本题要求你实现一个稍微更值钱一点的 AI 英文问答程序,规则是:
无论用户说什么,首先把对方说的话在一行中原样打印出来;
消除原文中多余空格:把相邻单词间的多个空格换成 1 个空格,把行首尾的空格全部删掉,把标点符号前面的空格删掉;
把原文中所有大写英文字母变成小写,除了 I;
把原文中所有独立的 can you、could you 对应地换成 I can、I could—— 这里“独立”是指被空格或标点符号分隔开的单词;
把原文中所有独立的 I 和 me 换成 you;
把原文中所有的问号 ? 换成惊叹号 !;
在一行中输出替换后的句子作为 AI 的回答。
输入格式:
输入首先在第一行给出不超过 10 的正整数 N,随后 N 行,每行给出一句不超过 1000 个字符的、以回车结尾的用户的对话,对话为非空字符串,仅包括字母、数字、空格、可见的半角标点符号。
输出格式:
按题面要求输出,每个 AI 的回答前要加上 AI: 和一个空格。
输入样例:
6
Hello ?
Good to chat with you
can you speak Chinese?
Really?
Could you show me 5
What Is this prime? I,don 't know
输出样例:
Hello ?
AI: hello!
Good to chat with you
AI: good to chat with you
can you speak Chinese?
AI: I can speak chinese!
Really?
AI: really!
Could you show me 5
AI: I could show you 5
What Is this prime? I,don 't know
AI: what Is this prime! you,don't know
实验代码:
https://www.cnblogs.com/pkgunboat/p/10651822.html
这个题目自己不会写,听搭档说也听不明白。直接从网上找的代码,但是看不怎么懂。
7-3 ***八皇后问题 (20 分)
在国际象棋中,皇后是最厉害的棋子,可以横走、直走,还可以斜走。棋手马克斯·贝瑟尔 1848 年提出著名的八皇后问题:即在 8 × 8 的棋盘上摆放八个皇后,使其不能互相攻击 —— 即任意两个皇后都不能处于同一行、同一列或同一条斜线上。
现在我们把棋盘扩展到 n × n 的棋盘上摆放 n 个皇后,请问该怎么摆?请编写程序,输入正整数 n,输出全部摆法(棋盘格子空白处显示句点“.”,皇后处显示字母“Q”,每两格之间空一格)。
输入格式
正整数 n (0 < n ≤ 12)
输出格式
若问题有解,则输出全部摆法(两种摆法之间空一行),否则输出 None。
要求:试探的顺序逐行从左往右的顺序进行,请参看输出样例2。
输入样例1
3
输出样例1
None
输入样例2
6
输出样例2
. Q . . . .
. . . Q . .
. . . . . Q
Q . . . . .
. . Q . . .
. . . . Q .
. . Q . . .
. . . . . Q
. Q . . . .
. . . . Q .
Q . . . . .
. . . Q . .
. . . Q . .
Q . . . . .
. . . . Q .
. Q . . . .
. . . . . Q
. . Q . . .
. . . . Q .
. . Q . . .
Q . . . . .
. . . . . Q
. . . Q . .
. Q . . . .
实验代码:
https://blog.csdn.net/sinat_37059404/article/details/75371145
思路
这个题目也不会写
定义数组,模拟棋盘和皇后;摆放旗子,放好第一颗棋子之后第二颗棋子从可行的位置从小到大的顺序尝试,以后是棋子摆放位置以此类推;用一个有92行每行8个元素的二维数组记录可行的摆放方法。然后后面就不知道了。