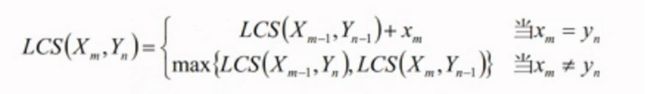回溯算法
回溯法:也称为试探法,它并不考虑问题规模的大小,而是从问题的最明显的最小规模开始逐步求解出可能的答案,并以此慢慢地扩大问题规模,迭代地逼近最终问题的解。这种迭代类似于穷举并且是试探性的,因为当目前的可能答案被测试出不可能可以获得最终解时,则撤销当前的这一步求解过程,回溯到上一步寻找其他求解路径。
为了能够撤销当前的求解过程,必须保存上一步以来的求解路径,这一点相当重要。
-
八皇后问题
8皇后问题是其经典的问题,描述为:在一个 8x8的国际象棋棋盘中,怎样放置8个皇后才能使8个皇 后之间不会互相有威胁而共同存在于棋局中,即在8x8个格子的棋盘中没有任何两个皇后是在同一行、同一列、同一斜线上。
思路:用回溯法,最容易想到的方法就是有序地从第 1 列的第 1 行开始,尝试放上一个皇后,然后再尝试第 2 列的第几行能够放上一个皇后,如果第 2 列也放置成功,那么就继续放置第 3 列,如果此时第 3 列没有一行可以放置一个皇后,说明目前为止的尝试是无效的(即不可能得到最终解),那么此时就应该回溯到上一步(即第 2 步),将上一步(第 2 步)所放置的皇后的位置再重新取走放在另一个符合要求的地方…如此尝试性地遍历加上回溯,就可以慢慢地逼近最终解。
我们用代码模拟该步骤,比较简单的是使用递归方法
package com.fredal.structure;
public class NQueen {
static int index=0;
private static void show(int[] queen){
for(int i=0;i可以得到共有92种解法,我们注意到使用递归方法回溯的思想体现的不那么明显,因为递归是内部自动回溯的,效率也比非递归低一点的,所以我们又使用循环来模拟
关键在于如何回溯以及回溯的时机,冲突了需要回溯,同时找到一个解之后仍然需要回溯,这点值得注意!
package com.fredal.structure;
public class NQueen {
static int index=0;
private static void show(int[] queen){
for(int i=0;i8皇后问题扩展到n皇后问题是非常简单的,这儿就不做了.
-
迷宫问题
迷宫问题也是回溯法的经典应用,我们用代码模拟过程
package com.fredal.structure;
import java.util.HashSet;
import java.util.Set;
import com.fredal.structure.Maze.Position;
public class Maze {
char maze[][];//存放迷宫
Position entry;//入口
Position exit;//出口
Set res=new HashSet();//找到的解
//位置类
class Position{
int row;
int col;
public Position(int row,int col){
this.row=row;
this.col=col;
}
public int hashCode() {
return row*1000+col;
}
public boolean equals(Object obj) {
if(obj instanceof Position==false) return false;
Position p=(Position) obj;
return p.row==row && p.col==col;
}
public String toString() {
return "Position [row=" + row + ", col=" + col + "]";
}
}
public Maze(){
init();
}
//初始化迷宫
private void init(){
//硬编码迷宫
String[] x={
"####A#######",
"####....####",
"####.####..#",
"#....#####.#",
"#.#####.##.#",
"#.#####.##.#",
"#.##.......#",
"#.##.###.#.#",
"#....###.#.#",
"##.#.###.#.B",
"##.###...###",
"############"
};
maze=new char[x.length][];
for(int i=0;i path){
if(cur.equals(exit)) return true;//找到出口了
path.add(cur);//path存放所有的路
Position[] t={new Position(cur.row, cur.col-1),new Position(cur.row, cur.col+1),
new Position(cur.row-1, cur.col),new Position(cur.row+1,cur.col)
};//通过上下左右检测
for(int i=0;i();//存放所有的路
findPath(entry, path);
}
//打印迷宫
public void show(){
for(int i=0;i 和8皇后问题一样,我们发现递归其实是内部回溯,就是你在外面没有自己去回溯,回溯思想没有很好地体现,还有效率问题.
迷宫问题我们可以采用栈来完美地模拟,并且很好地体现了回溯的思想,我对每一步都调用了show(),所以每一步的走法和如何回退都非常清晰.
package com.fredal.structure;
import java.util.HashSet;
import java.util.Set;
import java.util.Stack;
import com.fredal.structure.Maze.Position;
public class MazeL {
char maze[][];//存放迷宫
Position entry;//入口
Position exit;//出口
Position cur;//当前位置
Stack res=new Stack();
//位置类
class Position{
int row;
int col;
public Position(int row,int col){
this.row=row;
this.col=col;
}
public int hashCode() {
return row*1000+col;
}
public boolean equals(Object obj) {
if(obj instanceof Position==false) return false;
Position p=(Position) obj;
return p.row==row && p.col==col;
}
public String toString() {
return "Position [row=" + row + ", col=" + col + "]";
}
}
public MazeL(){
init();
}
//初始化迷宫
private void init(){
//硬编码迷宫
String[] x={
"####A#######",
"####....####",
"####.####..#",
"#....#####.#",
"#.#####.##.#",
"#.#####.##.#",
"#.##.......#",
"#.##.###.#.#",
"#....###.#.#",
"##.#.###.#.B",
"##.###...###",
"############"
};
maze=new char[x.length][];
for(int i=0;i0&&maze[cur.row][cur.col-1]!='#'&&maze[cur.row][cur.col-1]!='x'){
cur=new Position(cur.row, cur.col-1);
show();
}
else if(cur.col+1<12&&maze[cur.row][cur.col+1]!='#'&&maze[cur.row][cur.col+1]!='x'){
cur=new Position(cur.row, cur.col+1);
show();
}
else if(cur.row-1>0&&maze[cur.row-1][cur.col]!='#'&&maze[cur.row-1][cur.col]!='x'){
cur=new Position(cur.row-1, cur.col);
show();
}
else if(cur.row+1<12&&maze[cur.row+1][cur.col]!='#'&&maze[cur.row+1][cur.col]!='x'){
cur=new Position(cur.row+1, cur.col);
show();
}
else{//四条路都走不通
show();
if(!res.isEmpty()){
res.pop();//回溯
cur=res.peek();
res.pop();//弹两次是因为一开始还要push进来
}
}
}
return false;
}
//打印迷宫
public void show(){
for(int i=0;i 随机化算法
随机化算法,在算法中使用随机函数,其中决策依赖于某种随机事件,基本特征是同一个实例用统一随机化算法得到可能完全不同的结果.
-
随机数生成器
首先当然要产生随机数啦.随机数在概率算法中扮演着十分重要的角色,现实计算机上无法产生真正的随机数,都是在一定程度上随记的,即伪随机.
产生随机数最常用的是线性同余法.数x1,x2,...的生成满足:Xi+1=A Xi mod M.刚开始给出的值X0称为种子.这里我们一般取M为31比特数即2147483647,取A为48271这个素数.据此我们可以设计算法
package com.fredal.structure;
public class Random {
private static final int A=48271;
private static final int M=Integer.MAX_VALUE;
private static final int Q=(M/A);
private static final int R= (M%A);
private int state;
public Random(){//使用系统时间与inf的余数作为种子
state=(int) (System.currentTimeMillis()%Integer.MAX_VALUE);
}
public int RandomInt(){
int tmpState=A*(state%Q)-R*(state/Q);
if(tmpState>=0) state=tmpState;
else state=tmpState+M;
return state;
}
public double Random0_1(){//产生0-1之间的随机数
return (double)RandomInt()/M;
}
public static void main(String[] args) {
Random m=new Random();
for(int i=0;i<20;i++){
System.out.println(m.Random0_1());
}
}
}
这里最关键的问题在于Q和R是啥,还有RandomInt()的里面按照公式直接返回(A*state)%M不行么,嗯,这个问题在于乘法可能溢出.解决溢出虽然可以使用64比特的long,但是减慢计算速度.
于是Schrage给出了算法,计算M/A的商和余数并分别定义为Q和R,那么按照程序中的算法,可以确保不溢出.推导可以查相关资料.
注: 接下去本节默认使用上面实现的随机数产生器
-
数值概率算法
顾名思义,这个,就是最简单直接的随机化算法.
比较有趣的例子是用概率模拟去求π的值,众所周知,在边长为a的正方形内部画一个最大的四分之一圆,面积是πa²/4,那么与正方形面积之比是π/4,很容易算出π的值.
怎么算面积只比呢,那就是概率模拟咯
package com.fredal.structure;
public class Pi {
//假设边长为1的正方形
public static double go(Random r,long n){
long k=0;
for(long i=0;i比较有趣的一点是,除了100次1000次这种实在不太靠谱之外,并不是次数越多就越精确的噢!!不相信可以多实验几次.
-
舍伍德算法(Sherwood)
舍伍德算法的公式推导,复杂度计算啥的可以参考维基百科,这里说一下基本思想:在一般输入数据的程序里,输入多多少少会影响到算法的计算复杂度。这时可用舍伍德算法消除算法所需计算时间与输入实例间的这种联系.
舍伍德算法总能求得问题的一个解,且所求得的解总是正确的。当一个确定性算法在最坏情况下的计算复杂性与其在平均情况下的计算复杂性有较大差别时,可以在这个确定算法中引入随机性将它改造成一个舍伍德算法,消除或减少问题的好坏实例间的这种差别。舍伍德算法精髓不是避免算法的最坏情况行为,而是设法消除这种最坏行为与特定实例之间的关联性。
它可以获得很好的平均性能,很典型的例子就是之前我们说的快速排序,参考快速排序.选取标杆时第一种是无脑选取第一个,还有是我们采用了三数中值法,当然随记选取标杆也是很自然的想法.
这里现在上面写的随记类中加一个方法
//0-n的随记整数
public int Random(int n){
return (int) (Random0_1()*(n+1));
}
可以开始写了
package com.fredal.structure;
public class Sherwood {
public static void main(String[] args) {
Random r=new Random();
int[] a={14,7,2,34,6,95,27,9,54,12,103};
quickSort(a, 0, a.length-1,r);
for(int i=0;i=x) j--;//从右向左找第一个小于x的数
if(i 当然舍伍德算法有局限性,很多情况下所给的确定性算法无法直接改造成舍伍德算法,这时候可以借助随机预处理技术,仅对输入进行随机洗牌,同样可以达到舍伍德算法的效果.
还是就快速排序说,随记选取标杆确实是一个方法,但是在排序前对数组随机洗牌一次,再选第一个作为标杆,也是一样的嘛..
package com.fredal.structure;
import java.util.Arrays;
public class Sherwood {
public static void main(String[] args) {
Random r=new Random();
int[] a={14,7,2,34,6,95,27,9,54,12,103};
quickSort(a, 0, a.length-1,r);
show(a);
}
//随记洗牌算法
public static void shuffle(int[] a,Random r){
int len=a.length;
for(int i=0;i=x) j--;//从右向左找第一个小于x的数
if(i -
拉斯维加斯算法(Las Vegas)
同样只说一下基本思想:拉斯维加斯算法不会得到不正确的解。一旦用拉斯维加斯算法找到一个解,这个解就一定是正确解。但有时用拉斯维加斯算法找不到解.所以通常用一个布尔函数来表示
void Obstinate(InputType x, OutputType y){
// 反复调用拉斯维加斯算法LV(x, y),直到找到问题的一个解
boolean success= false;
while (!success)
success = LV(x,y);
}
设p(x)是对输入x调用拉斯维加斯算法获得问题的一个解的概率,t(x)是算法obstinate找到具体实例x的一个解所需的平均时间,s(x)和e(x)分别是算法对于具体实例x求解成功或求解失败所需的平均时间.
容易得到:t(x)=p(x)s(x)+(1-p(x))(e(x)+tx(x)),可以解得t(x)=s(x)+((1-p(x))/p(x))e(x)
我们在回溯法的时候讲过8皇后问题,之前是从0往后递增地放,并采用回溯.但其实每个皇后在棋盘山位置无规律,不具有系统性,用拉斯维加斯算法十分自然.
从第0行开始,每一行得皇后摆放的位置都是随记的,如果摆放不了冲突了就全盘否定掉重新开始,而不是采用回溯往前退一步.由于我们是采用随记的算法,所以仍然有较高的概率找到解的.
要讲的是这儿设计算法注意的问题.每一步放皇后的位置是随机的,很容易想到这么写:
while(!check(queen,k,i)){
i=r.Random(7);
}
其实这么写很容易理解,就是每一步检验通不过的时候就一直采取新的随机数.
但是会有一个问题,前几行也许没问题,但是假如这一行没有可以放的列,我们就一直死循环了,那怎么办,设置循环多少次之后就默认找不到了然后重新开始?
好吧刚开始确实掉死胡同里去,其实可以先遍历一遍这一行的所有列,在那些可行的列里面再进行随记选取.
package com.fredal.structure;
public class LVQueen {
private static void show(int[] queen){
for(int i=0;i0){//每一层
count=0;//置为0
for(int j=0;j<8;j++){//遍历所有列
if(check(queen, k, j))
can[count++]=j;
}
if(count>0)//说明可以找到存放的地方
queen[k++]=can[r.Random(count-1)];//可能存放的列里面随便选一个
}
return (count>0);
}
//测试新皇后放入的位置
private static boolean check(int[] queen,int row,int col){
for(int i=0;i 有兴趣的还可以测试一下成功率.当然其实纯粹采用拉斯维加斯算法也不是最好的,我们可以采取拉斯维加斯算法与回溯法相结合,即前几行用随机化,后几行开始用回溯法.
package com.fredal.structure;
public class LVQueen {
private static void show(int[] queen){
for(int i=0;i0){//每一层
count=0;//置为0
for(int j=0;j<8;j++){//遍历所有列
if(check(queen, k, j))
can[count++]=j;
}
if(count>0)//说明可以找到存放的地方
queen[k++]=can[r.Random(count-1)];//可能存放的列里面随便选一个
}
return (count>0);
}
//回溯法
public static void BackTrack(int[] queen,int k){
if(k==8){//找到解了
show(queen);
return;
}
for(int i=0;i<8;i++){
if(!check(queen, k, i))
continue;
else {
queen[k]=i;//放置皇后k
BackTrack(queen, k+1);//放置皇后k+1
queen[k]=-1;//更好地表示回溯 会被覆盖的
}
}
}
//测试新皇后放入的位置
private static boolean check(int[] queen,int row,int col){
for(int i=0;i 有兴趣地测试一下选取的stopVeags不同对成功率以及解的个数的影响,还有性能.笼统的说,当stopVeags为1和8的时候成功率应该是1,1的时候解有92个,8的时候就是1个.从2到7递增的话成功率是递减,解必然递减.性能的话按照我之前测试貌似是取2的时候最好.
除了著名的8皇后问题,来说一下寻找第k小的数这个问题,我们采用拉斯维加斯算法,很容易得到
package com.fredal.structure;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
public class FindTheKMin {
public static void main(String[] args) {
Integer[] a={12,56,73,45,9,51,43,67,11};
List lst=Arrays.asList(a);
while(!find(lst, 2)){
}
}
public static boolean find(List a,int index){
//Random r=new Random();//放到外面去...
int random=(int)(Math.random()*a.size());
int mid=a.get(random);//随记选择一个数
List s1=new ArrayList();
for(Integer x:a){//记录比mid数小的
if(x 这里有点小问题,不知道为什么用我自己写的随机数产生器性能低得令人发指(好吧我知道了,我怎么把随机数生成器放到方法里去了,随机性没了).但这个思路是没错的,就是随机选一个,看看是不是符合要求,不符合重新来一遍...
当然这个太暴力了,而且当我们要求的数有很多重复值的时候,成功率降低很多,我们还是加点优化,加点分治法之类的...
package com.fredal.structure;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
public class FindTheKMin {
public static void main(String[] args) {
Integer[] a={12,56,73,45,9,51,43,67,11};
List lst=Arrays.asList(a);
find(lst, 7);
}
static Random r=new Random();
public static void find(List a,int index){
int random=r.Random(a.size()-1);
int mid=a.get(random);//随记选择一个数
List s1=new ArrayList();
List s2=new ArrayList();
List s3=new ArrayList();
for(Integer x:a){//记录比mid数小的,相等的,大的
if(xmid)
s3.add(x);
}
if(s1.size()>=index)
find(s1,index);//说明在s1内
else if(s1.size()+s2.size()>=index){
System.out.println(mid);//说明在s2内
return;
}else if(s1.size()+s2.size() 其实这个我认为和拉斯维加斯算法差得有点远了,但是算法不用拘泥.当然也可以用舍伍德随即洗牌之类的算,每次先shuffle一下,一样的.
-
蒙特卡洛算法(Monte Carlo)
首先要讲一下,随机化算法之间并不是泾渭分明的,像之前随机投点法求π也算蒙特卡洛算法,只有蒙特卡洛算法与拉斯维加斯算法有着比较明显的区别,前者是以高概率给出正确解,但无法确定那个是不是正确解.后者是给出的解一定是正确的,但可能给不出...够明显的区别了吧...
基本思想:当所要求解的问题是某种事件出现的概率,或者是某个随机变量的期望值时,它们可以通过某种“试验”的方法,得到这种事件出现的频率,或者这个随机变数的平均值,并用它们作为问题的解。
公式推导啥的维基百科去,直接上例子
主元素问题:问题描述标准版自行谷歌,由于没弄好LaTeX,我感性地描述一下,就是一个元素要有很多重复,而且重复的数量超过整个数组的一半了,他就是主元素...
编码很简单:
package com.fredal.structure;
public class Major {
static Random r=new Random();
private static boolean MajorMC(int[] a){
int random=r.Random(a.length-1);
int x=a[random];//随记选取元素
int index=0;
for(int i=0;i(a.length/2)){
System.out.println(x);//顺便把主元素输出了
return (index>(a.length/2));//如果是主元素 概率大于1/2
}
return false;
}
public static boolean MajorMC(int[] a,double e){
int k = (int) Math.ceil(Math.log(1.0/e) / Math.log(2.0));//e表示错误的概率
for(int i=0;i 思路很简单,就是随机选取一个数,如果有主元素的话,那么这个数不是主元素的概率小于1/2.至于重复选取多少次呢,我们程序中e为错误的概率,那么显然我们只调用一次的话,出错概率为0.5.想要降低到e的概率,那么应该调用log(1/e)次算法(以2为底).可以自行推导.
然后讲一讲素性测试,在前面,我们讲过了筛法求素数,参考筛法求素数.
素性测试基于两个定理:费马小定理,以及关于平方探测定理.
费马小定理:如果P是素数,且0
于是我们需要平方探测定理:如果P是素数且0
对于m=41=101001,b5b4b3b2b1b0=101001,可以这样来求a^m:
初始C=1.
b5=1:C=C^2(=1),∵b5=1->C=aC(=a);
b5b4=10:C=C2(=a2),∵b4=0,不做动作;
b5b4b3=101:C=C2(=a4),∵b3=1,做C=aC(=a^5);
b5b4b3b2=1010:C=C2(=a10),∵b2=0,不做动作;
b5b4b3b2b1=10100:C=C2(=a20),∵b1=0,不做动作;
b5b4b3b2b1b0=101001:C←C2(=a40),∵b0=1->C=a*C(=a^41)。
完了之后我们还要对a^(n-1)对n求模,那么显然我们可以在每一步动作后就求模,而不用等全部算完才求模.还有一点,中间的算平方步骤可以完美地进行平方探测.一举两得.
package com.fredal.structure;
public class IsPrime {
//计算a^i mod n
private static long witness( long a, long i, long n )
{
if( i == 0 )
return 1; //二进制最高位,开始回退
long x = witness( a, i / 2, n );//递归调用
if( x == 0 ){//如果递归回来的是0 说明之前平方探测失败 直接返回就行了
return 0;
}
long y = ( x * x ) % n;//顺带平方探测!,注意是顺带,二进制求次方的关键
if( y == 1 && x != 1 && x != n - 1 )//表示平方探测失败
return 0;
if( i % 2 != 0 )
y = ( a * y ) % n;//二进制如果是1 就再乘以一次a再取模
return y;
}
static Random r = new Random( );
public static boolean isPrime( long n )
{
for( int counter = 0; counter < 10; counter++ )//反复调用10次
if( witness( r.randomLong( 2, n - 2 ), n - 1, n ) != 1 )
return false;
return true;
}
public static void main( String [ ] args )
{
for(int i=500;i<600;i++){
if(isPrime(i))
System.out.println(i);
}
}
}
动态规划(Dynamic Programming)
动态规划是通过拆分问题,定义问题状态和状态之间的关系,使得问题能够以递推(或者说分治)的⽅式去解决.
动态规划最重要的两个要点:
- 状态(状态不太好找,可先从转化方程分析)
- 状态间的转化方程(从问题的隐含条件出发寻找递推关系)
动态规划:适用于子问题不是独立的情况,也就是各子问题包含公共的子子问题,鉴于会重复的求解各子问题,DP对每个问题只求解一遍,将其保存在一张表中,从而避免重复计算.
-
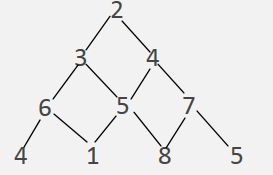
自顶向下求最短路径
如图求自顶向下的最短路径,可以知道最短路径为
2-3-5-1
首先我们用二维数组triangle来存储,变成了
[
[2],
[3,4],
[6,5,7],
[4,1,8,3]
]
我们设f(x,y)表示从(0,0)到(x,y)的最短路径和,那么状态转移方程为;
f(x,y) = min{f(x − 1,y),f(x − 1,y − 1)} + triangle[x][y],初始状态为f(0,0).
当然我们也可以选择自底向上考虑,f(x,y)表示出发走到最后一行的最短路径和,那么状态转移方程为:
f(x,y) = min{f(x + 1,y),f(x + 1,y + 1)} + triangle[x][y],初始状态为f(n-1,y).
我们可以依次编码实现,首先是自顶向下:
package com.fredal.structure;
import java.util.Arrays;
public class TopToBottom {
public static int minimum(int[][] t){
int n=t.length;
int[][] result=new int[n][n];//存放结果
result[0][0]=t[0][0];//初始化条件
for(int i=1;i0 && j 接着是自底向上考虑,按照转状态移方程可得:
package com.fredal.structure;
public class BottomToTop {
public static int minimum(int[][] t){
int n=t.length;
int[][] result=new int[n][n];//存放结果
for(int i=0;i=0;i--){
for(int j=0;j<=i;j++){
result[i][j]=min(result[i+1][j], result[i+1][j+1])+t[i][j];//状态转移方程
}
}
return result[0][0];//顶部就是最小值
}
private static int min(int i, int j) {
return i 这种方式虽然思维逆向一点,但编码方便一点.
-
LCS(最长公共子序列)
该问题描述如下:一个数列 S,如果分别是两个或多个已知数列的子序列,且是所有符合此条件序列中最长的,则 S 称为已知序列的最长公共子序列。
例如:输入两个字符串 BDCABA 和ABCBDAB,字符串 BCBA 和 BDAB 都是是它们的最长公共子序列,则输出它们的长度 4,并打印任意一个子序列.
稍加推理可以得出递归结构的方程:
设C[i,j]记录Xi和Yj的最长子序列的长度,则可以得到如下状态转移方程:
算出的c[i][j]数组以及如何选择子序列如图:
用代码模拟可得所有子序列:
package com.fredal.structure;
import java.util.LinkedList;
public class LCS {
private static Character[] result;
public static int[][] LCS(char[] X,char[] Y){
int[][] c=new int[X.length+1][Y.length+1];//存放最长子序列长度,长度加1是因为 第一行第一列拿来初始化了
//第一行第一列 自动初始化为0
for(int i=1;i<=X.length;i++){
for(int j=1;j<=Y.length;j++){
if(X[i-1]==Y[j-1])
c[i][j]=c[i-1][j-1]+1;
else if(c[i-1][j]>=c[i][j-1])
c[i][j]=c[i-1][j];
else
c[i][j]=c[i][j-1];
}
}
return c;
}
//打印最长子序列 使用递归
public static void print(int[][] c,char[] x,char[] y,int i,int j,int len){
if(i==0||j==0){//找到解了 就进行输出
for(int k=0;kc[i][j-1])
print(c, x, y, i-1, j,len);
else if(c[i-1][j] 要注意的是存放长度的数组应为字符数组长度加1,因为多余一列拿来初始化状态.还有打印所有结果的时候,本来想用链表存储子序列,这样push,pop比数组方便一点,但是链表在各个递归之间会相互影响,用数组则不会出现这种问题.
-
最大子段和
就是一段数字数组,求出连续的和最大的字段.注意要连续,设b[j]为子段和,a[j]为每个数,那么很简单的得出状态方程是
b[j]=max(b[j-1]+a[j],a[j]),1<=j<=n
主要就看当b[j-1]>0时b[j]=b[j-1]+a[j],否则b[j]=a[j]
package com.fredal.structure;
import java.util.LinkedList;
public class MaxSubSum {
public static void maxSum(int[] a){
int n=a.length;
int sum=0,b=0;//初始化最大子段和为0
LinkedList start=new LinkedList();
int flag=0,end=0;//设置子段位置参数
for(int i=0;i0)
b+=a[i];
else{
b=a[i];
start.push(i);//更新开始下标
flag=1;
}
System.out.println(b);
if(b>sum){
sum=b;//更新最大子段和
end=i;
flag=0;
}
if(flag==1)//如果更新了开始下标,但却没有改变sum值,说明是错误的更新
start.pop();
}
System.out.println("最大子段和是:从"+(start.pop()+1)+"到"+(end+1)+",和为"+sum);
}
public static void main(String[] args) {
int[] a={1,2,6,-7,-3,-4};
maxSum(a);
}
}
这问题求子段和不难,求两端坐标想了好一会儿,要注意b=a[i]时候更新开始下标有可能是错误的!.
-
LIS(最长递增子序列)
问题描述:找出一个n个数的序列的最长单调递增子序列: 比如A = {5,6,7,1,2,8,3,4,5} 的LIS是1,2,3,4,5.
我不得不吐槽,我认为很多书,网上的博客都存在错误,而会对初学者造成误导.
首先LIS[i] 是以arr[i]为末尾的LIS序列的长度(这个概念并不正确,只是为了解决问题设置的一个量)
可以得到LiS[i]=max(1,max(LIS(j)+1));jLiS[i]=max(LIS(j))+1,醉了.回过头来虽然这个状态转移方程对于解决问题是对的,只是和上面的概念是有冲突的)
那么按照序列是5,6,7,1,2,8,3,4,5,根据状态方程计算LIS[1...i]应该为1,2,3,1,2,4,3,4,5.看到冲突的地方了么,按照概念到1为止即LIS[4]应该为3,但是按照方程应该为1,而且只有按照后者计算结果才是对的.不啰嗦了给代码:
package com.fredal.structure;
public class LIS {
public static void LIS(int[] a){
int[] result=new int[a.length];
int maxlen=0;//LIS长度
for(int i=0;ia[j] && result[i]maxlen)
maxlen=result[i];
}
System.out.println("最长上升子序列长度为:"+maxlen);
}
public static void main(String[] args) {
int[] a={5,6,7,1,2,9,3,4,5};
LIS(a);
}
}
这个算法的复杂度是O(n²),也不方便给出LIS序列(可以设置前驱什么的),下面给出复杂度是O(n log n)的算法.
我们需要一个数组B[]来记录LIS的长度以及序列中最大的值.初始化B[0]为arr[0],接着如果arr数组中的数比B数组中最大的数,即末尾数大的话就添加到后面,否则就在数组B中找一个刚好比自己大的数(用二分实现),取代它.B数组的长度就是LIS的长度,但注意B数组并不是LIS...
package com.fredal.structure;
import java.util.Arrays;
public class LIS {
public static void show(int[] a){
for(int i=0;iB[blen-1]){
System.out.println(arr[i]+"插入");
B[blen++]=arr[i];//比B中最大的元素大 就接在后面
show(B);
}
else{
System.out.println(arr[i]+"替换");
B[binarySearch(B, arr[i],blen)]=arr[i];//找一个刚刚比其大的元素,取代他的位置
show(B);
}
}
return blen;
}
// 在数组中查找一个元素刚刚大于arr[i]
// 返回这个元素的index
public static int binarySearch(int []arr, int n,int blen){
int begin=0;
int end=blen-1;
while(begin<=end){
int mid = begin+(end-begin)/2;
if(arr[mid]==n)
return mid;
else if(arr[mid]>n)
end=mid-1;
else
begin=mid+1;
}
return begin;
}
public static void main(String[] args) {
int[] a={5,6,7,1,2,9,3,4,5};
System.out.println("最长上升子序列长度为"+LCSS(a));
}
}
为了理解方便,每一步骤都进行输出,结果如下:
-
01背包问题
如果有4个物品[2, 3, 5, 7].如果背包的大小为11,可以选择[2, 3, 5]装入背包,最多可以装满10的空间.如果背包的大小为12,可以选择[2, 3, 7]装入背包,最多可以装满12的空间.已知背包空间,函数需要返回最多能装满的空间大小
这是个典型的01背包问题,设F[i,v]表示前i件物品恰好放入容量为v的背包所获得的最大价值,第i件物品大小为Ci,价值为Wi,则其状态转移方程为:
F[i,v]=max(F[i-1,v],F[i-1,v-Ci]+Wi
只考虑第i件物品的策略(放或不放),那么就可以转化为一个只和前i − 1件物品相关的问题。如果不放第i件物品,那么问题就转化为“前i − 1件物品放入容量为v的背包中”,价值为F[i − 1, v];如果放第i件物品,那么问题就转化为“前i − 1件物品放入剩下的容量为v − Ci的背包中”,此时能获得的最大价值就是F[i − 1, v − Ci]再加上通过放入第i件物品获得的价值Wi。
而在此题中,物品的大小与价值相当于是相等的.我们用代码模拟该问题:
package com.fredal.structure;
public class BackPack {
public static int backpack(int[] a,int v){
final int M=v;//背包空间
final int N=a.length;
int[][] f=new int[N+1][M+1];
for(int i=0;ij)//即j-a[i]<0,放不下 选择不放
f[i+1][j]=f[i][j];
else
f[i+1][j]=Math.max(f[i][j], f[i][j-a[i]]+a[i]);//看看放和不放哪个更优
}
}
return f[N][M];
}
public static void main(String[] args) {
int[] a={2,3,5,7};
System.out.println(backpack(a, 11));
}
}
仍然是四件物品,大小为[2, 3, 5, 7],它们的价值为[1, 5, 2, 4], 问如果是空间为10的背包,怎么装可以获得最大的价值.
这道题和前面那道差不多,多就多在他们的价值不等于他们的大小了.也很简单
package com.fredal.structure;
public class BackPack {
public static int backpack2(int[] a,int[] w,int v){
final int M=v;//背包空间
final int N=a.length;
int[][] f=new int[N+1][M+1];
for(int i=0;ij)//即j-a[i]<0,放不下 选择不放
f[i+1][j]=f[i][j];
else
f[i+1][j]=Math.max(f[i][j], f[i][j-a[i]]+w[i]);//看看放和不放哪个更优
}
}
return f[N][M];
}
public static void main(String[] args) {
int[] a={2,3,5,7};
int[] w={1,5,2,4};
System.out.println(backpack2(a,w,10));
}
}
背包问题还有特别多可以讲,完全背包,多重背包...以后有时间肯定要再细致好好地写一下算法.
更多内容以及相关下载访问扩展阅读