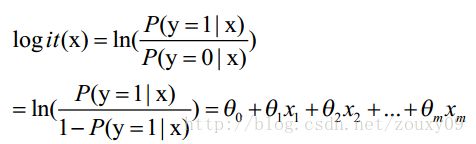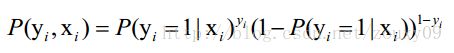待处理
统计学习方法:罗杰斯特回归及Tensorflow入门
参考阅读
深度学习笔记(一):logistic分类
Logistic Regression 的前世今生(理论篇)
Logistic Regression – Geometric Intuition
The Simpler Derivation of Logistic Regression
Logistic regression可以用来回归,也可以用来分类,主要是二分类。
logistic模型
角度一:logistic模型在伯努利分布和广义线性模型的假设下推导而来,逻辑回归也自然是一种广义线性模型。
指数族分布
指数族分布 (The exponential family distribution),区别于指数分布(exponential distribution)。在概率统计中,若某概率分布满足下式,我们就称之属于指数族分布。
其中η是natural parameter, T(y)是充分统计量, exp(−a(η))是起到归一化作用。 确定了T,a,b,我们就可以确定某个参数为η的指数族分布.
统计中很多熟悉的概率分布都是指数族分布的特定形式,如伯努利分布,高斯分布,多项分布(multionmal), 泊松分布等。下面介绍其中的伯努利分布和高斯分布。
伯努利分布
把伯努利概率模型修改成这种形式,可得:
其中:
同时我们可以看到ϕ=1/(1+exp(−η)), 居然是logistic sigmoid的形式。
在广义线性模型中,[图片上传失败...(image-b1c117-1513589177411)],可得前面![\phi ]的 Logistic 公式。
[图片上传失败...(image-4e16b7-1513589177411)]
广义线性模型,详细请见cs229的note
高斯分布
高斯分布也可以写为指数族分布的形式如下:
我们假设方差为1,当然不为1的时候也是可以推导的。上述我们就把高斯分布写为了指数族分布的形式,对应的
广义线性模型 (Generalized linear model, GLM)
本节将讲述广义线性模型的概念,以及LR,最小二乘为何也属于广义线性模型。
考虑一个分类或回归问题,我们就是想预测某个随机变量y,y是某些特征(feature)x
的函数。为了推导广义线性模式,我们必须做出如下三个假设
1. p(y|x;θ)服从指数族分布
2. 给了x, 我们的目的是为了预测T(y)的在条件x下的期望。一般情况T(y)=y, 这就意味着我们希望预测h(x)=E[y|x]
3. 参数η和输入x是线性相关的:η=θTx
在这三个假设(也可以理解为一种设计)的前提下,我们可以推导出一系列学习算法,称之为广义线性模型(GLM)。下面举两个例子:
最小二乘法
假设p(y|x;θ)∼N(μ,σ2), u可能依赖于x,那么
第一行因为假设2,第二行因为高斯分布的特点,第三行根据上面高斯分布为指数族分布的推导,第四行因为假设3
逻辑回归 logistic模型
考虑LR二分类问题,y∈0,1, 因为是二分类问题,我们很自然的选择p(y|x;θ)~Bernoulli(ϕ),即服从伯努利分布。那么
第一行因为假设2,第二行因为伯努利分布的性质,第三行因为伯努利分布为指数族分布时的推导,第四行因为假设3.
所以我们终于知道逻辑回归LR
从何而来了。它即是在伯努利分布和广义线性模型的假设下推导而来,逻辑回归也自然是一种广义线性模型。
角度二:
假设我们的样本是{x, y},y是0或者1,表示正类或者负类,x是我们的m维的样本特征向量。那么这个样本x属于正类,也就是y=1的“概率”可以通过下面的逻辑函数来表示:
这里 θ是模型参数,也就是回归系数,σ是sigmoid函数。实际上这个函数是由下面的对数几率(也就是 x属于正类的可能性和负类的可能性的比值的对数)变换得到的:
LogisticRegression最基本的学习算法是最大似然
假设我们有n个独立的训练样本{(x1, y1) ,(x2, y2),…, (xn, yn)},y={0, 1}。那每一个观察到的样本(xi, yi)出现的概率是:
上面为什么是这样呢?当y=1的时候,后面那一项是不是没有了,那就只剩下x属于1类的概率,当y=0的时候,第一项是不是没有了,那就只剩下后面那个x属于0的概率(1减去x属于1的概率)。所以不管y是0还是1,上面得到的数,都是(x, y)出现的概率。那我们的整个样本集,也就是n个独立的样本出现的似然函数为(因为每个样本都是独立的,所以n个样本出现的概率就是他们各自出现的概率相乘):
那最大似然法就是求模型中使得似然函数最大的系数取值θ*。这个最大似然就是我们的代价函数(cost function)了。
变换下L(θ):取自然对数,然后化简。注:有xi的时候,表示它是第i个样本,得到:
这时候,用L(θ)对θ求导,得到:
角度三:
不是因为sigmoid函数好LR才用它,而是因为RL的建模过程就会计算出sigmoid
LR是一种线性分类方法,即用超平面[图片上传失败...(image-663812-1513589177411)]来分类。在二分类问题中,样本在超平面的一边就属于一类。这个超平面可以看作类与类之间的边界,如果一个样本出现在边界上,那么它必须同时满足
(1)
[图片上传失败...(image-7c41f8-1513589177411)]
(2)
[图片上传失败...(image-744ed-1513589177411)]
即边界上的样本属于边界两边的类的条件概率相等。考虑(2)与(3)是等价的
(3)
[图片上传失败...(image-87541e-1513589177411)]
联立(1)(3)有
(4)
[图片上传失败...(image-45cb4-1513589177411)]
我们知道由于类密度高斯假设和公共协方差假设,LDA(线性判别分析)是有这样的性质的,即LDA的log-odds是x的线性函数。而Logistic绕过了这2个假设直接以式(4)建模。尽管形式上和LDA是一样的,但是估计系数[图片上传失败...(image-1b918b-1513589177411)]的方法不同。logistic模型更具一般性,它认为一个样本属于类1的概率P(Y=1|x)大的话,它应当同时满足[图片上传失败...(image-dfe6e-1513589177411)]
类似的,当这个样本属于-1类概率 P(Y=-1|x)大时,应当同时满足[图片上传失败...(image-71b6e5-1513589177411)]
又由于样本属于两类的概率之和为1
图片上传失败...(image-16b02d-1513589177412)
联立(4)(5),解未知数为P(Y=1|x)和P(Y=-1|x)的方程得
[图片上传失败...(image-d502ad-1513589177412)][图片上传失败...(image-2a7983-1513589177412)]这就是LR,然后里边有sigmoid。
sigmoid函数可以来自于贝叶斯函数
为何要用sigmoid?
说到底源于sigmoid,或者说exponential family所具有的最佳性质,即maximum entropy的性质。maximum entropy可以给logistic regression一个很好的数学解释。
为什么maximum entropy好呢?entropy翻译过来就是熵,所以maximum entropy也就是最大熵。熵原本是information theory中的概念,用在概率分布上可以表示这个分布中所包含的不确定度,熵越大不确定度越大。所以大家可以想象到,均匀分布熵最大,因为基本新数据是任何值的概率都均等。
而我们现在关心的是,给定某些假设之后,熵最大的分布。也就是说这个分布应该在满足我假设的前提下越均匀越好。比如大家熟知的正态分布,正是假设已知mean和variance后熵最大的分布。
回过来看logistic regression,这里假设了什么呢?
首先,我们在建模预测 Y|X,并认为 Y|X 服从bernoulli distribution,所以我们只需要知道 P(Y|X);
其次我们需要一个线性模型,所以 P(Y|X) = f(wx)。
接下来我们就只需要知道 f 是什么就行了。
而我们可以通过最大熵原则推出的这个 f,就是sigmoid。
具体推导详见:http://www.win-vector.com/dfiles/LogisticRegressionMaxEnt.pdf
softmax
指数函数有放大和缩小的作用。指数级扩大最后一层的输出,每个值都会增大,然而最大的那个值相比其他值扩大的更多,然后归一化一下。
概率提供一种置信度或者频率。有了这些非确定性的指标,就可以指定对应的决策输出。
考虑任意多类(不仅是两类)的分类问题。
softmax回归
Exponential model 的形式是这样的:假设第i个特征对第k类的贡献是w_{ki},则数据点[图片上传失败...(image-2fd36b-1513589177412)]属于第k类的概率正比于[图片上传失败...(image-b8488b-1513589177412)]。
因为一个数据点属于各类的概率之和为1,所以可以得到[图片上传失败...(image-270097-1513589177412)]
现在回到两类(0、1)的情况,此时分母上只有两项:[图片上传失败...(image-cff75-1513589177412)]
分子、分母同除以分子,并设[图片上传失败...(image-46d854-1513589177412)],则有[图片上传失败...(image-d4ffb-1513589177412)]
其中参数[图片上传失败...(image-77f4e1-1513589177412)]表示第i个特征对1类的贡献比对0类的贡献多多少。
softmax 有其特殊性,只用于最后一层。其它的激活函数都是单输入单输出的,softmax 是多输入多输出的。
logistic回归与线性回归的不同点:
为了将线性回归输出的很大范围的数,例如从负无穷到正无穷,压缩到0和1之间,这样的输出值表达为“可能性”才能说服广大民众。
当然了,把大值压缩到这个范围还有个很好的好处,就是可以消除特别冒尖的变量的影响。而实现这个伟大的功能其实就只需要平凡一举,也就是在输出加一个logistic函数。
另外,对于二分类来说,可以简单的认为:如果样本x属于正类的概率大于0.5,那么就判定它是正类,否则就是负类。实际上,SVM的类概率就是样本到边界的距离,这个活实际上就让logistic regression给干了。
线性回归拟合的是输出,logistic拟合的是概率,线性回归输出可以是负无穷到正无穷,但是概率只能是0~1。
sigmoid和softmax区别
sigmoid和softmax通常来说是2类和多类分类采用的函数,但sigmoid同样也可以用于多类,不同之处在于sigmoid中多类有可能相互重叠,看不出什么关系,softmax一定是以各类相互排斥为前提,算出来各个类别的概率和为1。
binary cross-entropy和categorical cross-entropy是相对应的损失函数。
sigmoid 多分类可参考 Large-Scale Object Classification Using Label Relation Graphs(Jia Deng · Computer Vision @ University of Michigan,ECCV 14 best paper)
逻辑回归原理小结
scikit-learn 逻辑回归类库使用小结
在scikit-learn中,与逻辑回归有关的主要是这3个类。LogisticRegression, LogisticRegressionCV 和logistic_regression_path。
logistic_regression_path类则比较特殊,它拟合数据后,不能直接来做预测,只能为拟合数据选择合适逻辑回归的系数和正则化系数。主要是用在模型选择的时候。
正则化选择参数:penalty
LogisticRegression和LogisticRegressionCV默认就带了正则化项。penalty参数可选择的值为"l1"和"l2".分别对应L1的正则化和L2的正则化,默认是L2的正则化。
在调参时如果我们主要的目的只是为了解决过拟合,一般penalty选择L2正则化就够了。但是如果选择L2正则化发现还是过拟合,即预测效果差的时候,就可以考虑L1正则化。另外,如果模型的特征非常多,我们希望一些不重要的特征系数归零,从而让模型系数稀疏化的话,也可以使用L1正则化。
penalty参数的选择会影响我们损失函数优化算法的选择。即参数solver的选择,如果是L2正则化,那么4种可选的算法{‘newton-cg’, ‘lbfgs’, ‘liblinear’, ‘sag’}都可以选择。但是如果penalty是L1正则化的话,就只能选择‘liblinear’了。这是因为L1正则化的损失函数不是连续可导的,而{‘newton-cg’, ‘lbfgs’,‘sag’}这三种优化算法时都需要损失函数的一阶或者二阶连续导数。而‘liblinear’并没有这个依赖。
优化算法选择参数:solver
solver参数决定了我们对逻辑回归损失函数的优化方法,有4种算法可以选择,分别是:
a) liblinear:使用了开源的liblinear库实现,内部使用了坐标轴下降法来迭代优化损失函数。
b) lbfgs:拟牛顿法的一种,利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。
c) newton-cg:也是牛顿法家族的一种,利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。
d) sag:即随机平均梯度下降,是梯度下降法的变种,和普通梯度下降法的区别是每次迭代仅仅用一部分的样本来计算梯度,适合于样本数据多的时候。
从上面的描述可以看出,newton-cg, lbfgs和sag这三种优化算法时都需要损失函数的一阶或者二阶连续导数,因此不能用于没有连续导数的L1正则化,只能用于L2正则化。而liblinear通吃L1正则化和L2正则化。
同时,sag每次仅仅使用了部分样本进行梯度迭代,所以当样本量少的时候不要选择它,而如果样本量非常大,比如大于10万,sag是第一选择。但是sag不能用于L1正则化,所以当你有大量的样本,又需要L1正则化的话就要自己做取舍了。要么通过对样本采样来降低样本量,要么回到L2正则化。
从上面的描述,大家可能觉得,既然newton-cg, lbfgs和sag这么多限制,如果不是大样本,我们选择liblinear不就行了嘛!错,因为liblinear也有自己的弱点!我们知道,逻辑回归有二元逻辑回归和多元逻辑回归。对于多元逻辑回归常见的有one-vs-rest(OvR)和many-vs-many(MvM)两种。而MvM一般比OvR分类相对准确一些。郁闷的是liblinear只支持OvR,不支持MvM,这样如果我们需要相对精确的多元逻辑回归时,就不能选择liblinear了。也意味着如果我们需要相对精确的多元逻辑回归不能使用L1正则化了。
分类方式选择参数:multi_class
multi_class参数决定了我们分类方式的选择,有 ovr和multinomial两个值可以选择,默认是 ovr。
ovr即前面提到的one-vs-rest(OvR),而multinomial即前面提到的many-vs-many(MvM)。如果是二元逻辑回归,ovr和multinomial并没有任何区别,区别主要在多元逻辑回归上。
OvR的思想很简单,无论你是多少元逻辑回归,我们都可以看做二元逻辑回归。具体做法是,对于第K类的分类决策,我们把所有第K类的样本作为正例,除了第K类样本以外的所有样本都作为负例,然后在上面做二元逻辑回归,得到第K类的分类模型。其他类的分类模型获得以此类推。
而MvM则相对复杂,这里举MvM的特例one-vs-one(OvO)作讲解。如果模型有T类,我们每次在所有的T类样本里面选择两类样本出来,不妨记为T1类和T2类,把所有的输出为T1和T2的样本放在一起,把T1作为正例,T2作为负例,进行二元逻辑回归,得到模型参数。我们一共需要T(T-1)/2次分类。
从上面的描述可以看出OvR相对简单,但分类效果相对略差(这里指大多数样本分布情况,某些样本分布下OvR可能更好)。而MvM分类相对精确,但是分类速度没有OvR快。
如果选择了ovr,则4种损失函数的优化方法liblinear,newton-cg, lbfgs和sag都可以选择。但是如果选择了multinomial,则只能选择newton-cg, lbfgs和sag了。
类型权重参数: class_weight
class_weight参数用于标示分类模型中各种类型的权重,可以不输入,即不考虑权重,或者说所有类型的权重一样。如果选择输入的话,可以选择balanced让类库自己计算类型权重,或者我们自己输入各个类型的权重,比如对于0,1的二元模型,我们可以定义class_weight={0:0.9, 1:0.1},这样类型0的权重为90%,而类型1的权重为10%。
如果class_weight选择balanced,那么类库会根据训练样本量来计算权重。某种类型样本量越多,则权重越低,样本量越少,则权重越高。
那么class_weight有什么作用呢?在分类模型中,我们经常会遇到两类问题:
第一种是误分类的代价很高。比如对合法用户和非法用户进行分类,将非法用户分类为合法用户的代价很高,我们宁愿将合法用户分类为非法用户,这时可以人工再甄别,但是却不愿将非法用户分类为合法用户。这时,我们可以适当提高非法用户的权重。
第二种是样本是高度失衡的,比如我们有合法用户和非法用户的二元样本数据10000条,里面合法用户有9995条,非法用户只有5条,如果我们不考虑权重,则我们可以将所有的测试集都预测为合法用户,这样预测准确率理论上有99.95%,但是却没有任何意义。这时,我们可以选择balanced,让类库自动提高非法用户样本的权重。
提高了某种分类的权重,相比不考虑权重,会有更多的样本分类划分到高权重的类别,从而可以解决上面两类问题。
当然,对于第二种样本失衡的情况,我们还可以考虑用下一节讲到的样本权重参数: sample_weight,而不使用class_weight。sample_weight在下一节讲。
样本权重参数: sample_weight
上一节我们提到了样本不失衡的问题,由于样本不平衡,导致样本不是总体样本的无偏估计,从而可能导致我们的模型预测能力下降。遇到这种情况,我们可以通过调节样本权重来尝试解决这个问题。调节样本权重的方法有两种,第一种是在class_weight使用balanced。第二种是在调用fit函数时,通过sample_weight来自己调节每个样本权重。
在scikit-learn做逻辑回归时,如果上面两种方法都用到了,那么样本的真正权重是class_weight*sample_weight.
以上就是scikit-learn中逻辑回归类库调参的一个小结,还有些参数比如正则化参数C(交叉验证就是 Cs),迭代次数max_iter等,由于和其它的算法类库并没有特别不同,这里不多累述了。
| liblinear | lbfgs | newton-cg | sag | balance | sample_weight | |
|---|---|---|---|---|---|---|
| L1 | √ | × | × | × | √ | √ |
| L2 默认 | √ | √ | √ | √ | √ | √ |
| 样本量 | 无限制 | 无限制 | 无限制 | 样本量大于10万可选 ,样本量小尽量不要选 | class_weight使用balanced。 样本量越多,权重越小,样本量越少,权重越大 | 通过sample_weight来自己调节每个样本权重 |
| ovr 默认 | √ | √ | √ | √ | √ | √ |
| multinomial | × | √ | √ | √ | √ | √ |
参考文献
逻辑回归原理小结
李宏毅机器学习课程4~~~分类:概率生成模型
李宏毅机器学习课程5~~~分类:逻辑回归
机器学习算法与Python实践之(七)逻辑回归(Logistic Regression)
The equivalence of logistic regression and maximum entropy
models
广义线性模型cs229的note
多类分类下为什么用softmax而不是用其他归一化方法?
为什么机器学习的分类器用logistic模型?
为什么 LR 模型要使用 sigmoid 函数,背后的数学原理是什么?
Softmax vs. Softmax-Loss: Numerical Stability
Gradient Descent, Wolfe's Condition and Logistic Regression
机器学习算法之:指数族分布与广义线性模型