目录
- 一、什么是哈夫曼树(Huffman Tree)
- 1.1 哈夫曼树的定义
- 二、哈夫曼树的构造
- 2.1 哈夫曼树的特点
- 三、哈夫曼编码
- 3.1 使用二叉树编码
- 3.2 使用哈夫曼树编码
更新、更全的《数据结构与算法》的更新网站,更有python、go、人工智能教学等着你:https://www.cnblogs.com/nickchen121/p/11407287.html
一、什么是哈夫曼树(Huffman Tree)
如果我们将百分制的考试成绩转换成五分制的成绩,我们可以使用如下所示的程序:
/* c语言实现 */
if( score < 60 ) grade =1;
else if( score < 70 ) grade =2;
else if( score < 80 ) grade =3;
else if( score < 90 ) grade =4;
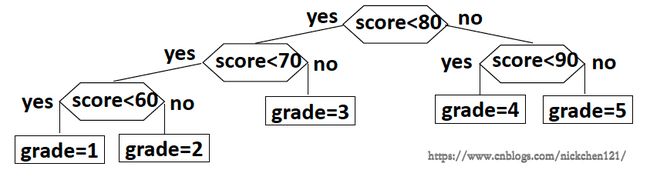
else grade =5;通过上述的代码,我们可以构造出如下图所示的判定树:
如果在上述五分制的成绩中,我们考虑学生成绩的分布的概率,如下图所示:
通过学生成绩分布的概率和上述的判定树,我们可以得到学生成绩的查找效率为:
\[ 0.05× 1+0.15 ×2+0.4× 3+0.3 ×4+0.1× 4 = 3.15 \]
从学生成绩分布的概率中,可以看出70-79和80-89分布中的学生较多,然而他们的查找效率确是较低的,因此我们可以按照如下方式修改代码和判定树:
/* c语言实现 */
if( score < 80 )
{
if( score < 70 );
if( score < 60 ) {
grade =1;
} else grade = 2;
else grad=3;
}
else if( score < 90 ) grade =4;
else grade =5; 通过此次修改,学生成绩的查找效率为:
\[ 0.05× 3+0.15 ×3+0.4× 2+0.3 ×2+0.1× 2 = 2.2 \]
通过上述的例子,我们可以思考一个问题:如何根据结点不同的查找频率构造更有效的搜索树?
1.1 哈夫曼树的定义
带权路径长度(WPL):设二叉树有n个叶子结点,每个叶子结点带有权值\(w_k\),从根节点到每个叶子结点的长度为\(l_k\),则每个叶子结点的带权路径长度之和就是:\(WPL = \sum_{k=1}^nw_kl_k\)
最优二叉树或哈夫曼树:WPL最小的二叉树
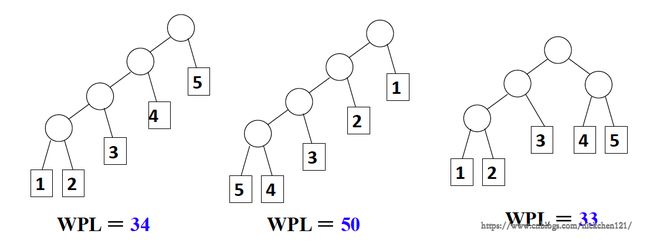
例:有五个叶子结点,它们的权值为 {1, 2, 3, 4, 5} ,用此权值序列可以构造出形状不同的多个二叉树。
二、哈夫曼树的构造
每次把权值最小的两颗二叉树合并
/* c语言实现 */
typedef struct TreeNode *HuffmanTree;
struct TreeNode{
int Weight;
HuffmanTree Left, Right;
}
HuffmanTree Huffman( MinHeap H )
{
// 假设H->Size个权值已经存在H->Elements[]->Weight里
int i; HuffmanTree T;
BuildMinHeap(H); // 将H->Elements[]按权值调整为最小堆
for (i = 1; i < H->Size; i++)
{
// 做H->Size-1次合并
T = malloc(sizeof(struct TreeNode)); // 建立新结点
T->Left = DeleteMin(H); // 从最小堆中删除一个结点,作为新T的左子结点
T->Right = DeleteMin(H); // 从最小堆中删除一个结点,作为新T的右子结点
T->Weight = T->Left->Weight+T->Right->Weight; // 计算新权值
Insert(H, T); // 将新T插入最小堆
}
T = DeleteMin(H);
return T;
} # python语言实现
# 节点类
class Node(object):
def __init__(self, name=None, value=None):
self._name = name
self._value = value
self._left = None
self._right = None
# 哈夫曼树类
class HuffmanTree(object):
# 根据Huffman树的思想:以叶子节点为基础,反向建立Huffman树
def __init__(self, char_weights):
self.a = [Node(part[0], part[1]) for part in char_weights] # 根据输入的字符及其频数生成叶子节点
while len(self.a) != 1:
self.a.sort(key=lambda node: node._value, reverse=True)
c = Node(value=(self.a[-1]._value + self.a[-2]._value))
c._left = self.a.pop(-1)
c._right = self.a.pop(-1)
self.a.append(c)
self.root = self.a[0]
self.b = list(range(10)) # self.b用于保存每个叶子节点的Haffuman编码,range的值只需要不小于树的深度就行
# 用递归的思想生成编码
def pre(self, tree, length):
node = tree
if (not node):
return
elif node._name:
print(node._name + '的编码为:')
for i in range(length):
print(self.b[i])
print()
return
self.b[length] = 0
self.pre(node._left, length + 1)
self.b[length] = 1
self.pre(node._right, length + 1)
# 生成哈夫曼编码
def get_code(self):
self.pre(self.root, 0)
if __name__ == '__main__':
# 输入的是字符及其频数
char_weights = [('a', 5), ('b', 4), ('c', 10), ('d', 8), ('f', 15), ('g', 2)]
tree = HuffmanTree(char_weights)
tree.get_code()上述过程的时间复杂度为:O(N logN)
2.1 哈夫曼树的特点
- 没有度为1的结点;
- n个叶子结点的哈夫曼树共有2n-1个结点
- 哈夫曼树的任意非叶结点的左右子树交换后仍是哈夫曼树;
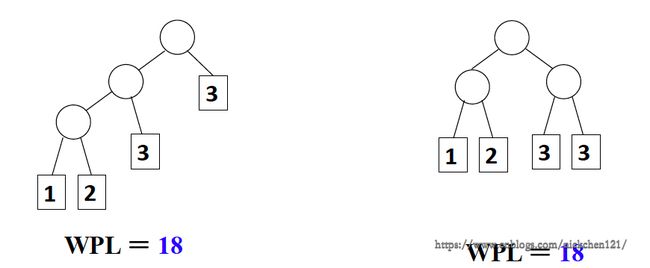
- 对同一组权值 \({W_1, W_2, \cdots, W_n}\),是否存在不同构的两颗哈夫曼树呢?
- 对一组权值 {1, 2, 3, 3},可以有如下图所示的不同构的两颗哈夫曼树:
三、哈夫曼编码
给定一段字符串,如何对字符进行编码,可以使得该字符串的编码存储空间最少?
例:假设有一段文本,包含58个字符,并由以下7个字符构成:a,e,i,s,t,空格(sp),换行(nl)。这7个字符出现的次数不同。如何对这7个字符进行编码,使得总编码空间最少?
分析:
- 用等长ASCCII编码:58*8 = 464位;
- 用等长3位编码:58*3 = 174位;
- 不等长编码:出现频率高的字符用的编码短些,出现频率低的字符可以编码长些?
对于上述问题,我们如果使用下图所示方式进行不等长编码:
很明显,可以发现上图所示的不等长编码具有二义性,因此我们可以使用前缀码的方式解决二义性问题。
前缀码(prefix code):任何字符的编码都不是另一字符编码的前缀。
3.1 使用二叉树编码
使用二叉树编码,我们需要注意以下两个问题:
- 左右分支:0、1
- 字符只在叶结点上
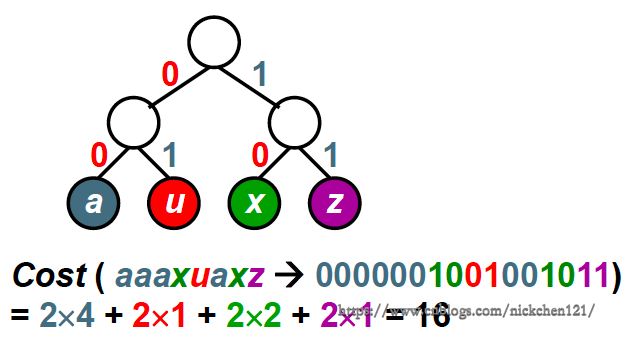
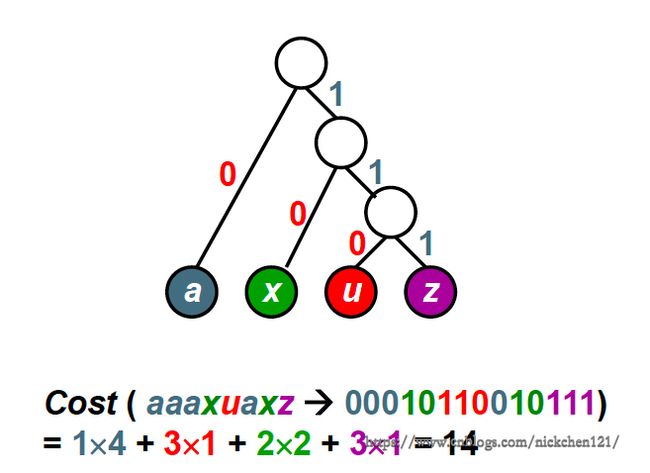
假设四个字符的频率为:a:4,u:1,x:2,z:1;那么我们可以使用最普通的二叉树对这四个字符进行编码,如下图所示:
通过上图可以发现,我们使用最偷懒的方式,把四个字符放在上述二叉树的四个叶子结点上,因此我们可以考虑使用如下所示的方法,降低二叉树的编码代价:
综上:哈夫曼编码需要解决的一个问题为——如何构造一颗编码代价最小的二叉树。
3.2 使用哈夫曼树编码
对于我们提出来的7个字符的例子,如果我们得知这7个字符的分布概率为如下图所示:
我们可以使用构造哈夫曼树的方式,进行哈夫曼编码,编码流程如下:
最终结果如下图所示: