序列标注（HMM/CRF）

简介

序列标注（Sequence Tagging）是一个比较简单的NLP任务，但也可以称作是最基础的任务。序列标注的涵盖范围是非常广泛的，可用于解决一系列对字符进行分类的问题，如分词、词性标注、命名实体识别、关系抽取等等。

对于分词相信看过之前博客的朋友都不陌生了，实际上网上已经有很多开源的中文分词工具，jieba、pkuseg、pyhanlp...这里都不一一列举了，我们也不再作过多的讨论。接下来都是以实体识别作为示例来讲解，而其他任务的实现都是基本一致，只是标注方式的不同罢了。

对于实体识别任务，我们有一段待标注的序列\(X = \{x_1, x_2,...,x_n\}\)，我们需要对该序列的每一个\(x_i\)预测一个对应的Tag，在通常情况下，我们对tag进行如下定义：

• B - Begin，表示开始
• I - Intermediate，为中间字
• E - End，表示结尾
• S - Single，表示单个字符
• O - Other，表示其他，用于标记无关字符

常见标签方案通常为三标签或者五标签法：

• IOB - 对于文本块的第一个字符用B标注，文本块的其它字符用I标注，非文本块字符用O标注
• IOBES - 对于文本块的第一个字符用B标注，文本块的最后一个字符用E标注，文本块的其它字符用I标注，非文本块用O标注

当然这样的tag并不是固定的，根据任务不同还可以对标签有一系列灵活的变化或扩展。对于分词任务，我们可以用同样的标注方式来标注每一个词的开头、结尾，或单字。如词性标注中，我们可以将标签定义为：n、v、adj...而对于更细类别的命名实体识别任务，我们在定义的标签之后加上一些后缀，如：B-Person、B-Location...这都可以根据你的实际任务来自行选择。

处理序列标注问题的常用模型包括隐马尔可夫模型（HMM）、条件随机场（CRF）、BiLSTM + CRF，由于篇幅的限制，这一节先介绍两个传统的机器学习模型：隐马尔可夫模型和条件随机场

隐马尔可夫模型（HMM）

HMM属于经典的机器学习算法，属于有向图模型的一种，主要用于时序数据建模。随着深度学习的发展，HMM在序列标注上用的比较少了，但也是做序列标注的一种基本思路。原理比较简单，已经掌握的同学可以跳过这一段，下面也只进行简单的介绍，想要详细了解的同学可以看看周志华老师的西瓜书，讲的非常详细的了。

HMM模型中的变量可以分为两组：

• 观测变量： \(X = \{x_1, x_2,...,x_n\}\)，用于表示第\(i\)个时刻的观测值
• 状态变量： \(Y = \{y_1, y_2,...,y_n\}\)，用于表示第\(i\)个时刻的隐藏状态，通常该状态是隐藏的，因此也称其为隐变量。
• 状态空间：\(S = \{s_1, s_2, ...,s_N\}\)，用于表示状态变量通常的取值范围。

显然，在序列标注任务中，待标注序列就对应观测变量，标注结果对应状态变量，而我们定义的标签类别就对应状态空间。对应的隐马尔可夫模型结构如下图所示：

上图的箭头表示变量间的依赖关系，即一种马尔可夫链结构，整个模型基于下面的隐马尔可夫假设：

• 在任一时刻，观测变量的取值仅仅依赖于状态变量，即\(x_t\)由\(y_t\)决定，与其他时刻的状态变量及观测变量无关（这就类似于一个unigram模型）, 即
  \[P(x_t|X, Y) = P(x_t|y_t)\]
• 在任一时刻，系统下一时刻的状态仅由当前状态决定，不依赖以往的任何状态，\(y_t\)仅与\(y_{t-1}\)有关，与其他都无关。这个假设意味着我们的隐变量是包含时序信息的，这是简单的分类模型所不具备的。即
  \[P(y_t|X, Y) = P(y_t|y_{t-1})\]

根据上述假设，则我们就可以对所有变量的联合概率分布进行建模：
\[P(x_1, y_1, ..., x_n, y_n)=P(y_1)P(x_1|y_1)\prod^n_{i=2}P(y_i|y_{i-1})P(x_i|y_i)\]

有了上述表达式，如果我们能够学习得到各个状态的初始概率\(P(y_1)\)，各个状态之间的转移概率\(P(y_i|y_{i-1})\)，以及观测概率\(P(x_i|y_i)\)，我们即可对任意序列计算得到我们的联合概率分布，从而选择最大概率的状态变量作为我们的预测结果。因此，HMM的主要有如下三组参数：

• 状态转移概率（Transition probabilities）：模型在各个状态之间转换的概率，通常记为矩阵\(A=[a_{i, j}]_{N \times N}\)，其中
  \[a_{i, j} = P(y_{t+1}=s_j|y_t=s_i), \sum_{i=1}^Na_{i, j}=1,1 \le i,j \le N\]
  • 其表示在任意时刻\(t\)，若状态为\(s_i\)，则下一时刻状态为\(s_j\)的概率
• 输出观测概率（Emission probabilities）：模型根据当前状态获得各个观测值的概率，通常记为矩阵\(B=[b_{i, j}]_{N \times M}\)，其中
  \[b_{i, j} = P(x_{t}=o_j|y_t=s_i), \sum_{i=1}^Nb_{i, j}=1, 1 \le i \le N, 1 \le j \le M\]
  • 其表示任意时刻\(t\)，若状态为\(s_i\)，则观测值\(o_j\)被获取的概率
• 初始状态概率（Start probabilities）：模型在初始时刻各个状态出现的概率，通常记为\(\pi = [\pi_1, \pi_2, ..., \pi_N]\)，其中
  \[\pi_i = P(y_1=s_i), \sum_{i=1}^N\pi_i=1, 1 \le i \le N\]

通常将其记为\(\lambda=[A, B, \pi]\)则联合概率分布即可化为如下表达式：
\[P(X, Y|\lambda) = \pi_{y_1}b_{y_1, x_1}\prod^n_{i=2}a_{y_{i-1}, y_i}b_{y_i, x_i}\]

概率图模型均存在三个基本问题，这也是我们求解概率图模型的基本步骤：

• 评估问题（Evaluation Problem）：给定\(\lambda\)和观测变量\(X\)，如何计算一个观测变量的概率\(P(X|\lambda)\)，用于评估模型与实际问题的匹配程度（前向后向算法）
• 学习问题（Learning Problem）：给定若干观测序列\(X\)，如何学习参数\(\lambda=[A, B, \pi]\)，使得计算出的\(P(X|\lambda)\)最大化（有监督下的极大似然估计）
• 解码问题（Decoding Problem）：给定\(\lambda\)和观测变量\(X\)，如何求出最可能的隐藏序列\(P(Y|X, \lambda)\)（维特比算法）

条件随机场（CRF）

HMM属于生成式模型，直接对联合分布\(P(X, Y)\)进行建模。CRF在某些方面与HMM有些类似，但属于一种判别式无向图模型，其对条件分布进行建模。具体来说，对于观测序列\(X\)和标记序列\(Y\)，CRF的目标就是构建条件概率模型\(P(Y|X)\)。

马尔可夫随机场

马尔可夫随机场又称为概率无向图模型，其表示一个联合概率分布。对于一个无向图模型\(G=[V, E]\)，\(V\)表示该无向图中的所有节点，\(E\)表示无向图中的所有无向边。如果无向图中各个节点之间的联合概率分布满足马尔可夫性，则称此联合概率分布为马尔可夫随机场或概率无向图模型。

马尔可夫性：任意节点对所有节点的条件概率分布等于其对其相邻节点的条件概率分布
\[P(y_v|Y_{V/{v}})=P(y_v|Y_{n(v)})\]

其中\(Y_{V/{v}}\)表示无向图中除\(y_v\)意外的所有节点，\(Y_{n(v)}\)表示与\(y_v\)相邻的所有节点。简单概括马尔可夫性就是不相邻节点之间条件独立，或每一个节点仅由相邻节点所决定。作为一个无向图模型，其没有HMM模型那样严格的假设

条件随机场

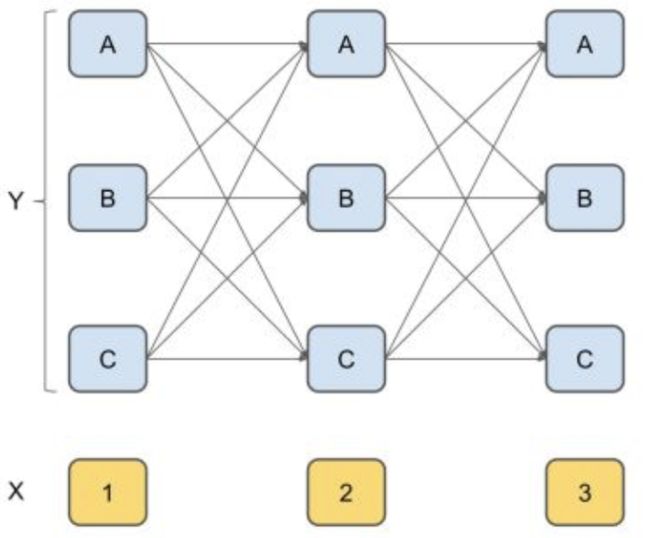
条件随机场为一种特殊的马尔可夫随机场，表示的是给定一组输入，得到的输出满足马尔可夫随机场。

对于我们的序列标注任务，我们所说的CRF通常都指链式CRF，如上图所示，即每个无向图模型为一个线性链模型，每一个节点仅与两个节点相邻，则每一个节点对所有节点的条件概率分布满足：
\[P(y_t|X, Y_{V/{v}}) = P(y_t|X, y_{t-1}, y_{t+1})\]

其中当\(t\)取\(1\)或\(n\)时只考虑单边。

条件随机场的特征函数

CRF对于条件概率\(P(Y|X)\)的建模是比较复杂的，但仔细看完下面的讲解你很快就能完全掌握了。条件随机场中的参数化形式的条件概率定义如下所示：
\[P(y|x)=\frac{1}{Z}exp(\sum_j\sum_{i=1}^{n-1}\lambda_it_j(y_{i+1}, y_i, x, i)+ \sum_k\sum_{i=1}^{n}\mu_ks_k(y_i, x, i))\]

其中：

• \(t_j(y_{i-1}, y_i, x, i)\)为局部特征函数，该特征由当前节点和上一个节点决定，称其为状态转移特征，用以描述相邻节点以及观测变量对当前状态的影响；
• \(s_k(y_i, x, i)\)为节点特征函数，该特征函数只和当前节点有关，称其为状态特征；
• \(\lambda\)和\(\mu\)是对应特征函数的参数。

在序列标注任务中，通常情况下，我们将其表示为条件随机场的矩阵形式，这更便于我们理解与计算：

对于链式条件随机场，我们首先定义两个特殊节点：\(y_0=\)，\(y_{n+1}=\)。
对观测序列\(X\)的每一个位置\(i = 1, 2, ..., n+1\)，定义一个N阶矩阵（N是隐藏状态的个数），这个矩阵等效于于HMM模型中的状态转移矩阵：
\[M_i(x)=[M_i(y_{i-1}, y_i|x)]\]

\[M_i(y_{i-1}, y_i|x)=exp(W_i(y_{i-1}, y_i|x))\]

\[W_i(y_{i-1}, y_i|x)=\sum_{k=1}^{K} w_kf_k(y_{i-1}, y_i, x, i)\]

其中\(f_k(y_{i-1}, y_i, x, i)\)是将状态转移特征\(t_j(y_{i-1}, y_i, x, i)\)以及状态特征\(s_k(y_i, x, i)\)统一化的符号表示，\(w_k\)为对应特征参数的统一化符号表征（详细的表征方法可以参考李航老师的《统计学习方法》的197页），这样，我们就得到了一个类似于HMM的状态转移矩阵，转移概率可以通过该序列n+1个矩阵适当元素的乘积表示，即\(\prod_{i=1}^{n+1}M_i(y_{i-1}, y_i|x)\)。但需要注意，这个状态转移矩阵\(M\)是非规范化的（所有概率累加不为1），我们可以归一化最后的条件概率为：
\[P_w(Y|X) = \frac{1}{Z_w(x)}\prod_{i=1}^{n+1}M_i(y_{i-1}, y_i|x)\]

其中：\(Z_w(x)=(M_1(x)M_2(x)...M_{n+1})_{start,stop}\)表示从开始状态到终止状态所有路径上的非规范化概率只和，即一个规范化因子，将非规范化概率规范化。

HMM的转移概率是受到约束的，而CRF的转移矩阵可以是任一权重，只需最后进行全局归一化就行了，这使得CRF较HMM显得更加灵活

CRF与HMM的对比

CRF较HMM更为强大，主要由如下几个原因：

• 每一个HMM都可以等效为一个特殊的CRF；
• CRF的隐藏状态可以依赖更广泛的信息（前后相邻的隐藏状态以及所有的观测变量），而HMM只能依赖上一个时刻的隐藏状态以及当前时刻的观测信息；
• CRF参数矩阵的取值没有限制（为非归一化概率），而HMM的参数取值需要受到限制。

维特比算法（Viterbi）

维特比算法用动态规划方法求解最短路径问题，可以用于HMM模型以及CRF模型的解码。

维特比算法需要如下三个元素：

• 初始状态概率\(\pi\)
• 状态转移概率
• 输出观测概率

由之前的介绍我们已经了解，这三个概率在HMM模型和CRF模型都为可求的。

算法基于这样一个思想：最优路径的子路径也一定是最优的。
举一个栗子就可以很清楚的明白了，假设我们有一个句子：“我爱北京天安门”。如果我们采用BIO的标注方法进行标注，则每个字的有3种可能的隐藏状态。我们按照以下的方法来求解每一层的条件概率：

• 求第一个字任一节点\(p_{1j}\)（每个节点对应一个隐藏状态）的初始状态概率，保存在该节点；
• 对第二个字的任一节点\(p_{2j}\)，利用第一层的每一个节点的概率以及对应的状态转移概率，计算出到每个上一层节点到\(p_{2j}\)的概率，并选择最大的概率及其对应的上一个节点保存在该节点，则我们记录了到达第二层每一个节点的最大概率以及对应的上一步位置。
• 对于第三个字的任一节点\(p_{3j}\)，利用第二层保存的最大概率及其转移概率，同样计算出每个上层节点到\(p_{3j}\)的概率，并选择最大的概率及其对应的上一个节点保存在该节点，则我们记录了到达第三层每一个节点的最大概率及上一步位置。
• 同理，后面每一层都利用上一层已有的最大概率及其转移概率，计算出当前层每一个最大的状态概率，并同时保存上一步的位置，直到最后一层。
• 到了最后一层，我们可以得到三个状态中概率最高的一个节点，别忘了，我们在存储最大概率的同时，还存储了上一个字的状态，这样，我们可以反向得到所有字对应的隐藏状态啦。

参考链接
https://blog.csdn.net/shuibuzhaodeshiren/article/details/85093765
https://www.cnblogs.com/Determined22/p/6750327.html
https://zhuanlan.zhihu.com/p/35620631
https://zhuanlan.zhihu.com/p/56317740
https://www.cnblogs.com/Determined22/p/6915730.html
https://zhuanlan.zhihu.com/p/63087935