本文简单整理了以下内容:
(一)线性回归
(二)二分类:二项Logistic回归
(三)多分类:Softmax回归
(四)广义线性模型
闲话:二项Logistic回归是我去年入门机器学习时学的第一个模型(忘记了为什么看完《统计学习方法》第一章之后直接就跳去了第六章,好像是对“逻辑斯蒂”这个名字很感兴趣?。。。),对照《机器学习实战》写了几行代码敲了一个toy版本,当时觉得还是挺有意思的。我觉得这个模型很适合用来入门(但是必须注意这个模型有很多很多很多很多可以展开的地方)。更有意思的是那时候还不会矩阵微积分,推导梯度时还是把矩阵全都展开求然后再归纳成矩阵形式的(牛顿法要用的二阶梯度也是)。。。
下面的文字中,“Logistic回归”都表示用于二分类的二项Logistic回归。
首先约定一下记号。
样本的特征矩阵 $X=(\textbf x_1,\textbf x_2,...,\textbf x_N)=({\textbf x^{(1)}}^{\top};{\textbf x^{(2)}}^{\top};...;{\textbf x^{(d)}}^{\top})\in\mathbb R^{d\times N}$ ,$X_{ji}=x_i^{(j)}$;
$N$ 是训练集的样本数,每个样本都表示成 $\textbf x_i\in\mathbb R^d$ 的列向量,真实标签为 $y_i$ ;如果出现了 $\textbf x$ 这样没有上下标的记号就泛指任一样本,相当于省略下标,真实标签为 $y$ ;特别地,对于二分类问题,$y$ 只可能取0、1两个值。
$d$ 是特征的维数,每维特征都表示成 $\textbf x^{(j)}\in\mathbb R^N$ 的列向量;如果出现了 $x^{(j)}$ 这样的记号就泛指任一样本的第 $j$ 维特征,相当于省略下标;
权重向量 $\textbf w=(w_1,w_2,...,w_d)^{\top}\in\mathbb R^d$ ,偏置 $b\in\mathbb R$ 。
$\textbf y$ 在本文可能表达两种含义:一种是表示全部训练样本的真实标签组成的列向量 $\textbf y=(y_1,y_2,...,y_N)^{\top}\in\mathbb R^N$ ;另一种含义则是表示样本 $\textbf x$ 的one-hot表示 $\textbf y=(0,0,...,0,1,0,...,0)^{\top}\in\mathbb R^C$(只有真实类别的那一维是1,其他维均是0),相当于 $\textbf y_i$ 省略了下标。
可能看起来有点别扭,因为对于样本来说,下标是序号索引、上标是特征索引;而对于权重来说,下标是特征索引。
(一)线性回归
1. 概述
线性回归(Linear regression)就是用一个超平面去拟合样本点的标签:
$$f(\textbf x)=\textbf w^{\top}\textbf x+b$$
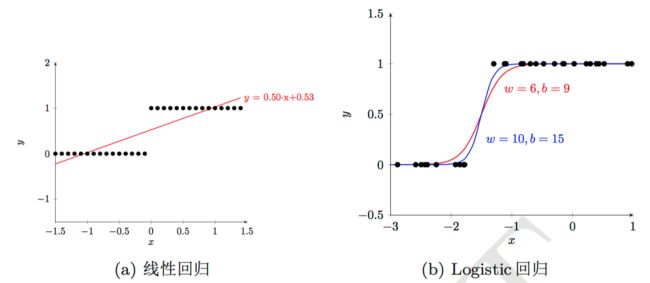
对于一维特征的情况,就是用一条直线去拟合样本点,如下图所示。为了方便起见,将偏置也记到权重向量中并保持记号不变,同时每个样本增加一维特征并保持记号不变:$\textbf w=(1,w_1,w_3,...,w_d)^{\top}$ ,$\textbf x=(1,x^{(1)},x^{(2)},...,x^{(d)})^{\top}$ ,$f(\textbf x)=\textbf w^{\top}\textbf x$ 。
图片来源:[1]
2. 求解
对于回归任务,最常使用的损失函数是平方损失函数 $L(y,f(\textbf x))=(y-f(\textbf x))^2$ ,对应的经验风险就是均方误差(Mean square error,MSE):
$$\mathcal R=\frac1N\sum_{i=1}^N(y_i-f(\textbf x_i))^2=\frac1N\|X^{\top}\textbf w-\textbf y\|^2=\frac1N(X^{\top}\textbf w-\textbf y)^{\top}(X^{\top}\textbf w-\textbf y)$$
该式的 $\textbf y$ 表示全部训练样本的真实标签组成的列向量 $\textbf y=(y_1,y_2,...,y_N)^{\top}\in\mathbb R^N$ 。
解一:正规方程组(Normal equations)。可以直接用 $R$ 的一阶导数等于0来求极值点(省略常系数):
$$\frac{\partial \mathcal R}{\partial\textbf w}=2X(X^{\top}\textbf w-\textbf y)=0\Rightarrow \textbf w=(XX^{\top})^{-1}X\textbf y$$
可以看出,这个不就是最小二乘法(Ordinary Least Squares,OLS)解方程 $X^{\top}\textbf w=\textbf y$ 嘛。值得注意的是 $(XX^{\top})^{-1}X$ 其实就是 $X^{\top}$ 的伪逆,计算伪逆的复杂度很高。
需要注意一个问题:$XX^{\top}$ 需要是可逆矩阵,也就是说每维特征之间线性无关,才可以求得唯一解。当其不可逆(特征个数比样本个数还要多)时,解不唯一,需要用梯度下降(Gradient descent)来迭代求解。另外,最小二乘法的结果总是低偏差高方差的。
(注:部分求导法则,使用分母布局,维度为 $q$ 的列向量对维度为 $p$ 的列向量求导后得到的矩阵维数为 $p\times q$ 。关于矩阵求导,可以参考 [8] 。
图片来源:[1]
$$\frac{\partial A^{\top}\textbf x}{\partial\textbf x}=\frac{\partial \textbf x^{\top}A}{\partial\textbf x}=A$$
$$\frac{\partial \textbf y^{\top}\textbf z}{\partial\textbf x}=\frac{\partial \textbf y}{\partial\textbf x}\textbf z+\frac{\partial \textbf z}{\partial\textbf x}\textbf y$$
$$\frac{\partial \textbf y^{\top}A\textbf z}{\partial\textbf x}=\frac{\partial \textbf y}{\partial\textbf x}A\textbf z+\frac{\partial \textbf z}{\partial\textbf x}A^{\top}\textbf y$$
$$\frac{\partial y\textbf z}{\partial\textbf x}=\frac{\partial y}{\partial\textbf x}\textbf z^{\top}+y\frac{\partial \textbf z}{\partial\textbf x}$$
$$\frac{\partial \text{tr}AB}{\partial A}=B^{\top}\quad\quad\frac{\partial \text{tr}AB}{\partial A^{\top}}=B$$
$$\frac{\partial f(A)}{\partial A^{\top}}=(\frac{\partial f(A)}{\partial A})^{\top}$$
)
解二:最小均方误差(least mean squares,LMS)规则,也叫Widrow-Hoff规则,用梯度下降法求解。梯度在上面已经求出来了:
$$\frac{\partial \mathcal R}{\partial\textbf w}=2X(X^{\top}\textbf w-\textbf y)=2X(\hat{\textbf y}-\textbf y)$$
该式的 $\hat{\textbf y}$ 表示模型对全部训练样本的输出标签组成的列向量 $\hat{\textbf y}=(\hat y_1,\hat y_2,...,\hat y_N)^{\top}\in\mathbb R^N$ 。
这样的方式是每更新一次参数就要计算整个训练集上的梯度,是批梯度下降(batch GD);如果把这个过程拆成 $N$ 次,也就是每次只随机挑选一个样本计算梯度,就是随机梯度下降(Stochastic GD,SGD)。还有一种是mini-batch梯度下降,每次挑选一个小批量样本计算梯度。整个训练集计算完一次梯度称为“一轮”。
3. 均方误差优化目标的概率解释
重新考虑以下问题:设样本的特征和标签存在关系 $y_i=\textbf w^{\top}\textbf x_i+\epsilon_i$ ,并假设每个 $\epsilon_i$ 都是服从高斯分布的随机变量 $\epsilon\sim N(0,\sigma^2)$ 的iid样本(之所以假设为高斯分布,是认为误差由多个独立的随机因素构成,根据多个独立随机变量之和趋于高斯分布,所以假设 $\epsilon$ 服从高斯分布)。从而有
$$p(\epsilon_i)=\frac1{\sqrt{2\pi}\sigma}\exp(-\frac{\epsilon_i^2}{2\sigma^2})$$
也就是说
$$p(y_i|\textbf x_i;\textbf w)=\frac1{\sqrt{2\pi}\sigma}\exp(-\frac{(y_i-\textbf w^{\top}\textbf x_i)^2}{2\sigma^2})$$
用分号隔开是因为在频率学派的观点下 $\textbf w$ 不是随机变量。
进一步用极大似然估计来求取参数 $\textbf w$ :对数似然函数为
$$l(\textbf w)=\log\prod_{i=1}^Np(y_i|\textbf x_i;\textbf w)=\log\prod_{i=1}^N\frac1{\sqrt{2\pi}\sigma}\exp(-\frac{(y_i-\textbf w^{\top}\textbf x_i)^2}{2\sigma^2})$$
再往后写一步就可以知道,极大似然估计和最小化均方误差是一致的。
4. 局部加权回归(Locally weighted regression,LWR)
相比于普通的线性回归,LWR对于一个点来说使用其附近的点来做回归(而不是全部点)。
相比于线性回归的优化目标 $\sum_{i=1}^N(y_i-\textbf w^{\top}\textbf x_i)^2$ ,局部加权线性回归的优化目标为
$$\sum_{i=1}^N\omega_i(y_i-\textbf w^{\top}\textbf x_i)^2$$
式中 $\omega_i$ 就是非负值的权重,一个常用的选择为 $\omega_i=\exp(-\frac{(\textbf x_i-\textbf x)^{\top}(\textbf x_i-\textbf x)}{2\tau^2})$ ,$\tau$ 是指定的带宽参数(bandwidth)。不难看出,LWR每预测一个点的值都要重新得到一个新的模型。
(二)二项Logistic回归
1. 概述
对于分类任务,一个可行的思路是把基于样本 $\textbf x$ 计算出的连续值 $z$(比如,线性加权值 $z=\textbf w^{\top}\textbf x$ )和离散的类别标签值联系起来。
二项Logistic回归(Binomial logistic regression)是工业界应用非常广泛的一个经典的二分类模型。一般就叫逻辑回归,这里无意争论到底应该怎么翻译,虽然古人云“名不正则言不顺”,但提起“逻辑回归”大家都知道这是哪个东西,我觉得这就够了。对Logistic回归的历史感兴趣的朋友们可以看一下 [7] 的介绍。首先使用logistic函数 $\sigma(\cdot)$ 将 $ z$ 从实数空间 $(-\infty,+\infty)$ 映射到概率空间 $(0,1)$ 上,可以将映射之后的值 $\sigma(z)$ 解释为样本 $\textbf x$ 属于正类(记类别标记为1)的可能性,也就是后验概率的估计值:
$$\hat y=P(y=1|\textbf x)=\sigma(z)=\frac{1}{1+\exp(-z)}$$
既然解释成后验概率,然后就可以给出分类规则(最大后验概率决策):当 $P(y=1|\textbf x)>0.5$ ,认为样本 $\textbf x$ 属于正类;否则样本 $\textbf x$ 属于正类属于负类。
下面两个图是一维特征、二分类的情况。大致说了线性回归为什么不可以用来分类。因为线性回归输出连续值,而类别标签只有0、1两个,所以需要人为设定一个阈值,将输出值与该值比较大小,从而来判断模型将样本分到哪一类,而这个阈值会受到离群点(outlier)的牵制,因为线性回归的拟合曲线会因为离群点而受到较大影响,所以不好确定;相比之下,logistic回归不会受到图示离群点的牵制。
图片来源:[5]、[1]
待补充:为什么使用logistic函数归到区间 $(0,1)$ 之后就可以解释成概率了。
2. 决策边界
下面说一下决策边界。当 $P(y=1|\textbf x)=0.5$ 时,意味着 $z=0$ ,这就是决策边界的方程。换句话说,$z$ 的形式决定了逻辑回归的决策面是线性的还是非线性的。如果 $z=\textbf w^{\top}\textbf x$ ,那决策面当然是线性的;但是如果 $z$ 的形式并不是特征的线性组合,而是非线性的形式,当然也可以是非常复杂的决策面。
图片来源:[1]
下面我们只讨论线性决策面的情况。Logistic回归模型为:
$$\hat y=P(y=1|\textbf x)=\sigma(\textbf w^{\top}\textbf x)=\frac{\exp(\textbf w^{\top}\textbf x)}{1+\exp(\textbf w^{\top}\textbf x)}$$
$$P(y=0|\textbf x)=1-\sigma(\textbf w^{\top}\textbf x)=\frac{1}{1+\exp(\textbf w^{\top}\textbf x)}$$
稍加变换就可以看出Logistic回归和线性回归的区别:
线性回归是用 $\textbf w^{\top}\textbf x$ 去拟合 $y$ ;二项Logistic回归则是去拟合 $\ln \dfrac{\hat y}{1-\hat y}$ ,换句话说就是在拟合对数几率(log-odds,几率是样本属于正类的可能性与属于负类的可能性的比值)。也就是说,二项Logistic回归在对对数几率做回归,进而转化为解决分类问题。
3. 求解
(1)经验风险最小化:极大似然估计
logistic函数 $\sigma(\cdot)$ 的导函数为 $\sigma'(\cdot)=\sigma(\cdot)\odot (\textbf 1-\sigma(\cdot))$ 。也就是说当自变量为向量时,函数对逐元素进行计算,输出同维度的向量。
首先从经验风险最小化的角度推导参数的求解过程。使用交叉熵损失函数(单标签情况下就是对数损失函数),模型对一个样本 $(\textbf x,y)$ 的对数损失为:
$$\begin{aligned}\mathcal L&=-\biggl(y\ln P(y=1|\textbf x)+(1-y)\ln P(y=0|\textbf x)\biggr)\\&=-\biggl(y\ln\frac{\exp(\textbf w^{\top}\textbf x)}{1+\exp(\textbf w^{\top}\textbf x)}+(1-y)\ln\frac{1}{1+\exp(\textbf w^{\top}\textbf x)}\biggr)\\&=-\biggl(y\textbf w^{\top}\textbf x-\ln(1+\exp(\textbf w^{\top}\textbf x))\biggr)\end{aligned}$$
所以经验风险为:
$$\mathcal R=\frac1N\sum_{i=1}^N\mathcal L_i=-\frac1N\sum_{i=1}^N\biggl(y_i\textbf w^{\top}\textbf x_i-\ln(1+\exp(\textbf w^{\top}\textbf x_i))\biggr)$$
如果不加正则的话,优化目标为上式最小化。前面的系数 $\dfrac1N$ 也就是训练样本数的倒数,是定值,去掉后不影响优化目标。
从极大似然估计的角度也可以推出等价的优化目标:对数似然函数为
$$\begin{aligned}l(\textbf w)&=\ln[\prod_{i=1}^NP(y_i|\textbf x_i;\textbf w)]\\&=\ln[\prod_{i=1}^NP(y_i=1|\textbf x_i)^{y_i}P(y_i=0|\textbf x_i)^{1-y_i}]\\&=\sum_{i=1}^N\biggl(y_i\ln P(y_i=1|\textbf x_i)+(1-y_i)\ln P(y_i=0|\textbf x_i)\biggr)\end{aligned}$$
该式最大化就等价于经验风险最小化。
由于优化目标求不出解析解,但它是高阶连续可微的凸函数,所以可以用迭代的方法,如梯度下降法(GD)。
因为SGD每次迭代是随机选择一个样本,所以这里先求取模型对一个样本的损失的梯度(经验风险的梯度无非就是加个求和号再除以训练样本数而已):
$$\frac{\partial \mathcal L}{\partial\textbf w}=-\biggl(y\textbf x-\textbf x\frac{\exp(\textbf w^{\top}\textbf x)}{1+\exp(\textbf w^{\top}\textbf x)}\biggr)$$
可以发现其实它就是个特别简单的形式:
$$\frac{\partial \mathcal L}{\partial\textbf w}=-(y-\hat y)\textbf x$$
经验风险的梯度可以写成矩阵的形式( $\textbf y$ 表示训练集样本的真实标签组成的列向量),省略系数 $\dfrac1N$ :
$$\begin{aligned}\frac{\partial \mathcal R}{\partial\textbf w}&=-\sum_{i=1}^N (y_i-\sigma(\textbf w^{\top}\textbf x_i))\textbf x_i\\&= -X(\textbf y-\sigma(X^{\top}\textbf w))\\&= -X(\textbf y-\hat{\textbf y})\end{aligned}$$
可以很容易把这种批处理GD的形式改写成mini-batch SGD的形式。
不难看出,这个梯度形式和线性回归是一样的。(后面会知道,Softmax回归的梯度形式和它们也是一样的。)
这里顺便把二阶梯度也求一下,可以使用牛顿法或拟牛顿法来迭代求取参数:
$$\frac{\partial \mathcal L}{\partial\textbf w}=-(y-\sigma(\textbf w^{\top}\textbf x))\textbf x=\sigma(\textbf w^{\top}\textbf x)\textbf x -y\textbf x$$
$$\begin{aligned}\frac{\partial^2\mathcal L}{\partial\textbf w^2}&=\frac{\partial(\sigma(\textbf w^{\top}\textbf x)\textbf x -y\textbf x)}{\partial\textbf w}\\&=\frac{\sigma(\textbf w^{\top}\textbf x)}{\partial\textbf w}\textbf x^{\top}\\&=\sigma(\textbf w^{\top}\textbf x)(1-\sigma(\textbf w^{\top}\textbf x))\textbf x\textbf x^{\top}\\&=\hat y(1-\hat y)\textbf x\textbf x^{\top}\end{aligned}$$
$$\frac{\partial^2\mathcal R}{\partial\textbf w^2}=\sum_{i=1}^N\hat y_i(1-\hat y_i)\textbf x_i\textbf x_i^{\top}$$
(2)结构风险最小化:最大后验概率估计
如果将正则项加上,那就是用结构风险最小化的准则来学习参数,常用的有参数的 $L_1$ 范数(LASSO)和 $L_2$ 范数(Ridge):
$$R_{\text{srm}}=R+\lambda\|\textbf w\|_1$$
$$R_{\text{srm}}=R+\lambda\|\textbf w\|_2^2$$
从梯度的形式来看,相比于不加正则的时候,变化量为
$$\frac{\partial \|\textbf w\|_1}{\partial w_j}=\frac{\partial \sum_{j=1}^d|w_j|}{\partial w_j}=1\text{ if }w_j>0\text{ else if }w_j<0\,-1$$
$$\frac{\partial \|\textbf w\|_2^2}{\partial w_j}=\frac{\partial \sum_{j=1}^d|w_j|^2}{\partial w_j}=2w_j$$
如果 $w_j$ 为正,那么新迭代点相比之前会减去一个正数而变小;如果 $w_j$ 为负,那么新迭代点相比之前会减去一个负数而变大。也就是说避免了特别大或者特别小的权重值出现,可以使权重的绝对值变小,从而避免过于依赖某些特征的情况,减轻过拟合。
加 $L_1$ 正则时会使某些维的参数变成0,这就是所谓的稀疏解,相当于进行了一个特征选择的过程;加 $L_2$ 正则时权重的绝对值会变小,起到平滑化的作用。更详细地可以参考[4]。
4. 贝叶斯角度
如果从贝叶斯估计的角度来说,正则项相当于加上了先验知识:加 $L_1$ 正则相当于是认为参数服从Laplace分布,加 $L_2$ 正则相当于是认为参数服从均值为0、协方差为 $\frac{1}{\lambda}$ 的高斯分布。此时,结构风险最小化等价于最大后验概率估计。具体可以参考[6][9]。
5. 与其他模型的关系
最显然的一个就是全连接的前馈神经网络就是多层Logistic回归模型(不知道为什么被叫成MLP,多层感知机)。其与朴素贝叶斯的联系可以看本系列博客第二篇。更详细地请参考 [7] ,后面有空的话会简单谈一点。
6. 并行
这里参考[7]。
(三)Softmax回归
Softmax回归可以用于多类分类问题,而不像Logistic回归等二分类模型那样需要借助One-vs-rest。设样本 $\textbf x_i$ 的真实类别标签 $y_i\in\{1,2,...,C\}$ ,one-hot向量为 $\textbf y_i=(0,0,...,0,1,0,...,0)^{\top}\in\mathbb R^C$ (只有真实类别的那一维是1)。
与Logistic回归类似,Softmax回归输出的是样本 $\textbf x_i$ 属于各个类别的后验概率的估计值 $P(y_i=c|\textbf x_i),c\in\{1,2,...,C\}$ :
$$z_c=\textbf w_c^{\top}\textbf x_i$$
$$\begin{aligned}P(y_i=c|\textbf x_i)&=\text{softmax}(z_c)\\&=\frac{\exp(z_c)}{\sum_{j=1}^C\exp(z_j)}\\&=\frac{\exp(\textbf w_c^{\top}\textbf x_i)}{\sum_{j=1}^C\exp(\textbf w_j^{\top}\textbf x_i)},\quad c\in\{1,2,...,C\}\end{aligned}$$
将模型对一个样本 $(\textbf x_i,\textbf y_i)$ 的后验概率估计组成列向量
$$\hat{\textbf y}_i=(P(y_i=1|\textbf x),P(y_i=2|\textbf x),...,P(y_i=C|\textbf x))^{\top}\in\mathbb R^C$$
并将各个类别的权重向量 $\textbf w_c\in\mathbb R^d$ 组成权重矩阵 $W=(\textbf w_1,\textbf w_2,...,\textbf w_C)\in\mathbb R^{d\times C}$ ,可以写成如下形式:
$$\textbf z_i=(z_1,z_2,...,z_C)^{\top}=W^{\top}\textbf x_i$$
$$\begin{aligned}\hat{\textbf y}_i&=\text{softmax}(\textbf z_i)=\frac{\exp(\textbf z_i)}{\sum_{j=1}^C\exp(z_j)}\\&=\frac{\exp(W^{\top}\textbf x_i)}{\sum_{j=1}^C\exp(\textbf w_j^{\top}\textbf x)}=\frac{\exp(W^{\top}\textbf x_i)}{\textbf 1^{\top}\exp(W^{\top}\textbf x_i)}\\&=\frac{\exp(\textbf z_i)}{\textbf 1^{\top}\exp(\textbf z_i)}\end{aligned}$$
使用交叉熵损失函数,模型对一个样本 $(\textbf x_i,\textbf y_i)$ 的损失为:
$$\mathcal L_i=-\textbf y_i^{\top}\ln\hat{\textbf y}_i=-\textbf y_i^{\top}\ln\text{softmax}(\textbf z_i)=-\textbf y_i^{\top}\ln\frac{\exp(\textbf z_i)}{\textbf 1^{\top}\exp(\textbf z_i)}$$
所以经验风险(省略系数 $\dfrac1N$ )为
$$\mathcal R=\sum_{i=1}^N\mathcal L_i=-\sum_{i=1}^N\biggl(\textbf y_i^{\top}\ln\text{softmax}(W^{\top}\textbf x_i)\biggr)$$
下面求取对一个样本 $(\textbf x_i,\textbf y_i)$ 的损失的梯度。先上结论:
$$\frac{\partial \mathcal L_i}{\partial\textbf w_c}=-[\textbf y_i-\hat{\textbf y}_i]_c\textbf x_i,\quad c\in\{1,2,...,C\}$$
$$\frac{\partial \mathcal L_i}{\partial W}=-\textbf x_i(\textbf y_i-\hat{\textbf y}_i)^{\top}$$
式中 $[\textbf y_i]_c$ 表示的是向量 $\textbf y_i$ 的第 $c$ 维元素的值。
经验风险的梯度依旧可以写成矩阵的形式:
$$\frac{\partial \mathcal R}{\partial W}=\sum_{i=1}^N\frac{\partial \mathcal L_i}{\partial W}=-X(Y-\hat Y)$$
其中 $Y\in\mathbb R^{N\times C}$ 是one-hot标签构成的矩阵,每一行都是一个样本的one-hot标签;$\hat Y$ 含义类似。
Softmax回归的 $\dfrac{\partial \mathcal L_i}{\partial\textbf w_c}$ 的形式和Logistic回归的 $\dfrac{\partial \mathcal L_i}{\partial\textbf w}$ 是一样的。
下面给出推导过程。
$\dfrac{\partial \mathcal L_i}{\partial\textbf w_c}$ 的求法有三种:
(1)普通方法,一步步推,可以参考我很早之前写的一篇讲word2vec的博客,我觉得写的还挺清楚的;
(2)[1] 中的方法,在第三章;
(3)[3] 中的方法,而且用这个方法可以直接把 $\dfrac{\partial \mathcal L_i}{\partial W}$ 求出来。
$\dfrac{\partial \mathcal L_i}{\partial W}$ 推导方式可以是用 $\dfrac{\partial \mathcal L_i}{\partial\textbf w_c}$ “拼”成对矩阵 $W$ 的梯度。下面使用 [3] 里面介绍的技巧,直接求对矩阵 $W$ 的梯度。
[3] 介绍的是这样形式的求导:已知矩阵 $X$ ,函数 $f(X)$ 的函数值为标量,求 $\dfrac{\partial f}{\partial X}$ 。一种典型的例子就是求取损失对权重矩阵的导数。
对于一元微积分,$\text{d}f=f'(x)\text{d}x$ ;多元微积分,$\text{d}f=\sum_i\dfrac{\partial f}{\partial x_i}\text{d}x_i=(\dfrac{\partial f}{\partial \textbf x})^{\top}\text{d}\textbf x$;由此建立矩阵导数和微分的联系:
$$\text{d}f=\sum_{i,j}\frac{\partial f}{\partial X_{ij}}\text{d}X_{ij}=\text{tr}((\frac{\partial f}{\partial X})^{\top}\text{d}X)$$
上式第二个等号成立是因为对于两个同阶方阵有 $\text{tr}(A^{\top}B)=\sum_{i,j}A_{ij}B_{ij}$ 。求解的流程就是,先求微分 $\text{d}f$ 表达式,然后再套上迹(因为标量的迹等于标量本身),然后再把表达式 $\text{tr}(\text{d}f)$ 和 $\text{tr}((\dfrac{\partial f}{\partial X})^{\top}\text{d}X)$ 进行比对,进而把 $\dfrac{\partial f}{\partial X}$ 给“挖”出来。
所以,问题就从求梯度转化成了求微分。求微分当然少不了很多法则和技巧,下面随着讲随着介绍。接下来就来求取Softmax回归中的 $\dfrac{\partial \mathcal L}{\partial W}$ (样本序号 $i$ 被省略)。
首先求取 $\text{d}\mathcal L$ 。
$$\begin{aligned}\mathcal L&=-\textbf y^{\top}\ln\frac{\exp(\textbf z)}{\textbf 1^{\top}\exp(\textbf z)}\\&=-\textbf y^{\top}(\textbf z-\ln\begin{pmatrix}\textbf 1^{\top}\exp(\textbf z) \\ \textbf 1^{\top}\exp(\textbf z) \\ \vdots \\ \textbf 1^{\top}\exp(\textbf z)\end{pmatrix})\quad \textbf 1^{\top}\exp(\textbf z)\text{是标量}\\&=\ln(\textbf 1^{\top}\exp(\textbf z))-\textbf y^{\top}\textbf z\end{aligned}$$
根据法则 $\text{d}(g(X))=g'(X)\odot\text{d}X$ 、$\text{d}(XY)=(\text{d}X)Y+X(\text{d}Y)$,可得
$$\text{d}(\ln(\textbf 1^{\top}\exp(\textbf z)))=\frac{1}{\textbf 1^{\top}\exp(\textbf z)}\odot\text{d}(\textbf 1^{\top}\exp(\textbf z))$$
$$\text{d}(\textbf 1^{\top}\exp(\textbf z))=\textbf 1^{\top}\text{d}(\exp(\textbf z))=\textbf 1^{\top}(\exp(\textbf z)\odot\text{d}\textbf z)$$
所以
$$\text{d}\mathcal L=\frac{\textbf 1^{\top}(\exp(\textbf z)\odot\text{d}\textbf z)}{\textbf 1^{\top}\exp(\textbf z)}-\textbf y^{\top}\text{d}\textbf z$$
现在可以套上迹,根据恒等式 $\text{tr}(A^{\top}(B\odot C))=\text{tr}((A\odot B)^{\top}C)=\sum_{i,j}A_{ij}B_{ij}C_{ij}$ ,可得
$$\begin{aligned}\text{d}\mathcal L&=\text{tr}(\frac{(\textbf 1\odot \exp(\textbf z))^{\top}\text{d}\textbf z}{\textbf 1^{\top}\exp(\textbf z)})-\text{tr}(\textbf y^{\top}\text{d}\textbf z)\\&=\text{tr}(\biggl(\frac{(\exp(\textbf z))^{\top}}{\textbf 1^{\top}\exp(\textbf z)}-\textbf y^{\top}\biggr)\text{d}\textbf z)\\&=\text{tr}((\hat{\textbf y}-\textbf y)^{\top}\text{d}\textbf z)\\&=\text{tr}((\frac{\partial L}{\partial\textbf z})^{\top}\text{d}\textbf z)\end{aligned}$$
现在已经成功了一半,因为已经有了 $\dfrac{\partial \mathcal L}{\partial\textbf z}$ 。因为
$$\text{d}\textbf z=\text{d}(W^{\top}\textbf x)=(\text{d}W^{\top})\textbf x+W^{\top}\text{d}\textbf x=(\text{d}W^{\top})\textbf x$$
并且 $\text{tr}(ABC)=\text{tr}(BCA)=\text{tr}(CAB)$ ,所以有
$$\begin{aligned}\text{d}\mathcal L&=\text{tr}((\frac{\partial L}{\partial\textbf z})^{\top}(\text{d}W^{\top})\textbf x)\\&=\text{tr}(\textbf x(\frac{\partial L}{\partial\textbf z})^{\top}\text{d}W^{\top})\\&=\text{tr}((\frac{\partial L}{\partial W^{\top}})^{\top}\text{d}W^{\top})\end{aligned}$$
也就是说,$\dfrac{\partial \mathcal L}{\partial W^{\top}}=\dfrac{\partial \mathcal L}{\partial\textbf z}\textbf x^{\top}=(\hat{\textbf y}-\textbf y)\textbf x^{\top}$,所以
$$\frac{\partial \mathcal L}{\partial W}=-\textbf x(\textbf y-\hat{\textbf y})^{\top}$$
(四)广义线性模型
其实上面介绍的三种模型,都属于广义线性模型(Generalized linear model,GLM)。
1. 指数族分布
说到GLM,就不得不说指数族分布。设有一随机变量 $Y$ ,观测值为 $y$ ,那么指数族分布(Exponential family distributions)的 PDF/PMF 为如下函数:
$$p(y;\boldsymbol\eta)=b(y)\exp(\boldsymbol\eta^{\top}T(y)-a(\boldsymbol\eta))$$
式中,$\boldsymbol\eta$ 被称为nature parameter或canonical parameter,$T(y)$ 是充分统计量(通常设 $T(y)=y$ ),$a(\boldsymbol\eta)$ 是log partition function,$\exp(-a(\boldsymbol\eta))$ 用来保证PDF的积分为1(或PMF的加和为1)。把随机变量服从指数族分布记为 $ Y\sim ExponentialFamily(\boldsymbol\eta)$ 。伯努利分布(两点分布)、高斯分布、多项式分布、泊松分布、指数分布、伽马分布、贝塔分布、狄利克雷分布、维希特分布……等等都属于指数族分布。
通过选取不同的 $\boldsymbol\eta$ ,可以得到不同的分布:
例如,对于参数为 $\phi$ 两点分布,其PMF为
$$P(y;\phi)=\phi^y(1-\phi)^{1-y}=\exp(y\ln(\frac{\phi}{1-\phi})+\ln(1-\phi))$$
所以
$$\phi=\frac{1}{1+\exp(-\eta)}$$
这正是logistic函数。
再比如参数为均值 $\mu$ 、方差1的高斯分布,其PDF为
$$p(y;\mu)=\frac{1}{\sqrt{2\pi}}\exp(-\frac12(y-\mu)^2)=\frac{1}{\sqrt{2\pi}}\exp(-\frac12y^2)\exp(\mu y-\frac12\mu^2)$$
所以
$$\mu=\eta$$
2. 广义线性模型
通过指数族分布,可以构建广义线性模型。设模型的参数为 $\boldsymbol\theta$ ,对于记 $X$ 、$Y$ 分别是代表特征和标签的随机变量,观测值为 $\textbf x$ 、$y$ 。首先假定如下三点:
1. 条件分布服从指数族分布,即 $Y|X;\boldsymbol\theta\sim ExponentialFamily(\boldsymbol\eta)$ 。例如,
2. 给定特征 $\textbf x$ ,目标是预测 $E[T(y)|\textbf x]$ 。因为通常设 $T(y)=y$ ,所以目标就是预测 $E[y|\textbf x]$ 。
实际上,就相当于对模型输出值进行预测。用Logistic回归举例:模型输出值为 $P(y=1|\textbf x)$ ,随机变量 $Y$ 服从两点分布(只可能取0、1两个值),所以 $E[y|\textbf x;\boldsymbol\theta]=0\times P(y=0|\textbf x)+1\times P(y=1|\textbf x)=P(y=1|\textbf x)$
3. 指数族分布的参数 $\boldsymbol\eta$ 和给定特征 $\textbf x$ 的关系为线性:$\boldsymbol\eta=\boldsymbol\theta^{\top}\textbf x$
下面可以开始利用不同的 $\boldsymbol\eta$ 来构建GLM。
(1)线性回归
对于第一个假设,设指数族分布是参数为 $\mu$ 的高斯分布,即 $\mu=\eta$ ;那么对于第二个假设,可知模型输出值为 $\mu$ ,结合第一个假设可知模型输出值为 $\eta$ ;根据第三个假设 $\boldsymbol\eta=\boldsymbol\theta^{\top}\textbf x$ ,可知模型输出值为 $\boldsymbol\theta^{\top}\textbf x$ 。这就推导出了线性回归模型。
(2)Logistic回归
对于第一个假设,设指数族分布是参数为 $\phi$ 的伯努利分布,即 $\phi=\frac{1}{1+\exp(-\eta)}$ ;那么对于第二个假设,因为伯努利分布的期望为 $\phi$ ,可知模型输出值为 $\phi$ ;根据第三个假设 $\boldsymbol\eta=\boldsymbol\theta^{\top}\textbf x$ ,可知模型输出值为 $\phi=\frac{1}{1+\exp(-\boldsymbol\theta^{\top}\textbf x)}$ 。这就推导出了Logistic回归模型。
(3)Softmax回归
相应的指数族分布是多项式分布,代表标签的是一个随机向量 $\boldsymbol Y$ 。详细的推导这里就不赘述了,可以参考 [5] 的最后一部分。
参考资料:
[1] 《神经网络与深度学习讲义》
[2] 《统计学习方法》
[3] 《矩阵求导术(上)》
[4] 机器学习中的范数规则化之(一)L0、L1与L2范数
[5] CS229 Lecture Notes1、Lecture6 slides
[6] Regularized Regression: A Bayesian point of view
[7] 浅析Logistic Regression (写的比我这篇真的好太多了。。。)
[8] Matrix_calculus
[9] https://www.evernote.com/shard/s146/sh/bf0d0a08-d5c5-4dc9-b70f-fa6374b9ceae/14e34bc9e8e518b1a5cc17fc585d75fc