如何评价模型的好坏（一）

• 二分类问题
• 多分类问题
• 连续变量问题

一、二分类问题

       二分类模型最常见的模型评价指标有：ROC曲线，AUC，精准率-召回率，准确率，F1-score，混淆矩阵，等。

假设检验

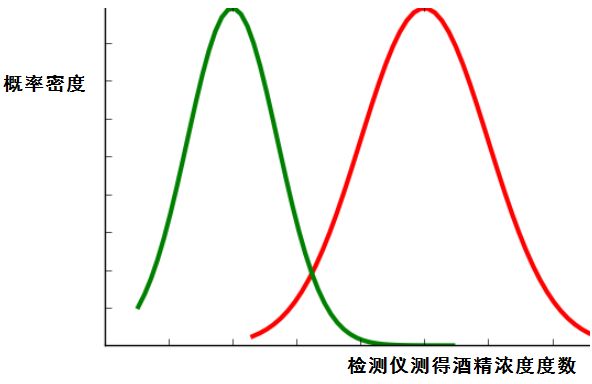
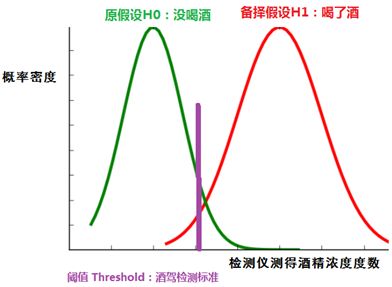
　　案例分析：（酒驾检测）酒精浓度检测结果分布图。（绿色：正常司机酒精浓度检测结果分布。红色：酒驾司机酒精浓度检测结果分布）   

引入三个概念：

• 原假设H0：没喝酒。       
• 备择假设H1：喝了酒。
• 阈值Threshold：酒驾检测标准（分类的阈值，阈值大小可人为改变）

• 阈值左边：接受原假设H0。 
• 阈值右边：拒绝原假设H0，接受备择假设H1。
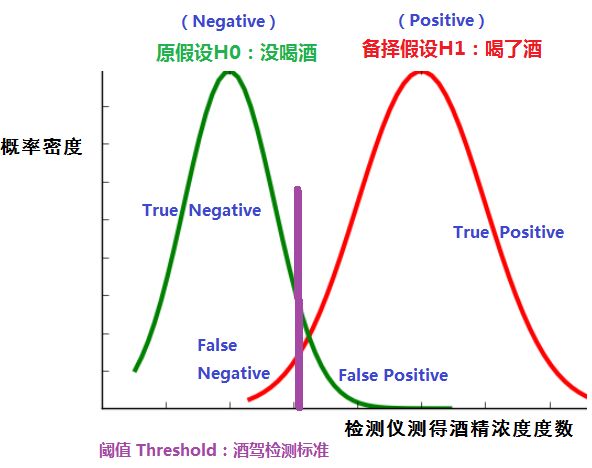
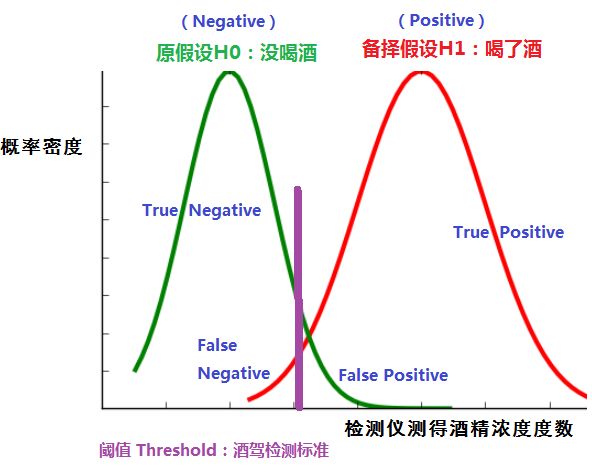
• 阈值的划分，产生四个值： True Positive、True Negative、False Positive（假阳性）、False Negative（假阴性），这四个值构成混淆矩阵。

　　一般默认：原假设成立---Negative， 备择假设成立---Positive

 

混淆矩阵

	检测：喝了酒（Positive）	检测：没喝酒（Negative）
实际：喝了酒	True Positive（TP）	False Negative（FN）
实际：没喝酒	False Positive（FP）	True Negative（FN）

 

 

 

 

 

统计学上，

　　第一类错误：（弃真）False Positive 假阳性

   　第二类错误：（存伪）False Negative 假阴性 

具体问题具体分析：

（1）医疗场景：可以容忍假阳性，但必须减少假阴性。（假阴性：某病人原本患某种疾病，却检测为没有生病）

（2）垃圾邮件识别：可以容忍假阴性，但必须减少假阳性。（假阳性：某个非常重要的邮件，被识别成垃圾邮件被删除，容易误事）

 

引入ROC曲线和AUC面积：

周志华《机器学习》33页：

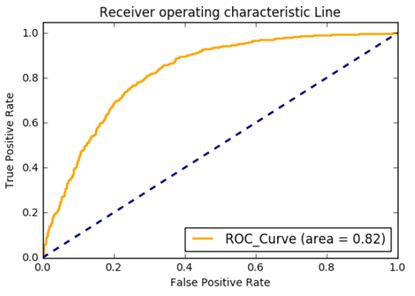
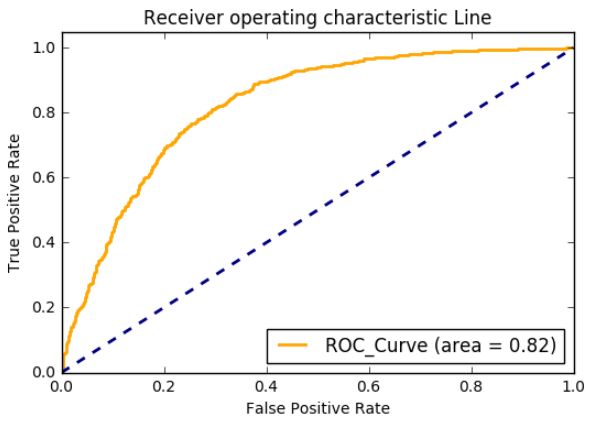
　　ROC 全称是“Receiver Operating Characteristic 曲线”，它源于“二战”中用于敌机检测的雷达信号分析技术，二十世纪六七十年代来时被用于一些心理学、医学检测应用中，此后被引入机器学习领域[Spackman，1989]。ROC曲线的纵轴是“真正例率”（True Positive Rate，简称TPR），横轴是“假正例率”（False Positive Rate，简称FPR）

                          　　　　　　   TPR = TP/(TP+FN)

                          　　　　　　   FPR = FP/(TN+FP)

 

从上图可以看出：

• TPR（真正例率）：TP + FN 表示：所有喝酒的人数，TP 表示：实际喝酒，被检测数喝酒的人数。
• FPR（假正例率）：TN + FP 表示：所有没有喝酒的人数， FP 表示：实际没喝酒，被检测出喝酒的人数。

总结：

1. ROC曲线单调递增，且每个点都在45度斜线上方（曲线面积大于0.5），意味着：TP > FP
2. ROC曲线的斜率始终为正，意味着：FP，TP同增同减（从酒精检测曲线图中可以观测到）
3. ROC曲线下方围成的面积值，就是 AUC（area under curve = AUC）
4. ROC曲线离45度斜线越远，表示分类效果越好。

 

引入准确率（accuracy）、召回率（recall）、精准率（precision）、F1-score：

（上文提到）混淆矩阵：

	检测：喝了酒（Positive）	检测：没喝酒（Negative）
实际：喝了酒	True Positive（TP）	False Negative（FN）
实际：没喝酒	False Positive（FP）	True Negative（FN）

 

 

 

 

 

（1）准确率： accuracy = (TP+TN) / (TP+FN+FP+TN)

• TP+FN+FP+TN 表示：所有接受酒精检测的人数。 TP+TN 表示：所有检测正确的人数。
• 准确率（accuracy）表示：所有实例中，分类正确的比例。

（2）召回率：recall = TP / (TP+FN)

• TP+FN 表示：实际喝了酒的人数， TP 表示：实际喝了酒，被检测出喝了酒的人数。
• 召回率（recall）表示：所有正例中分类正确的比例。

（3）精准率： precision = TP / (TP+FP)

• TP+FP 表示：被检测出喝了酒的人数， TP 表示：实际喝了酒，被检测出喝了酒的人数
• 精准率（precision）表示：被分为正例的示例中实际为正例的比例。 

 

分析：

　　对比：召回率（recall）和精准率（precision）两个公式，发现只有FN（假阴性）和FP（假阳性）表示不同。从酒精浓度检测曲线图中可以看出，FN 和 FP 不同增，即当 FN 增大时，FP会减少；当 FP 增加时，FN 会减少。 从而分析出，当 recall 增加时，precision 会减少；当precision 增加时，recall 会减少，“二者不可兼得”。为了平衡召回率（recall）和精准率（precision）两个指标，引入F-measure 和MAP（Mean Average Precision）

 

（4）F-measure = （1 + a²）* precision* recall / (a² * precision + recall)

• 当参数a = 1时，即为 F1-score。

（4-1）F1-score = 2/(1/R + 1/P) = 2* R* P/(R + P) 

• F1-score 表示 召回率 Recall（R）和精准率 Precision（P）的调和平均数

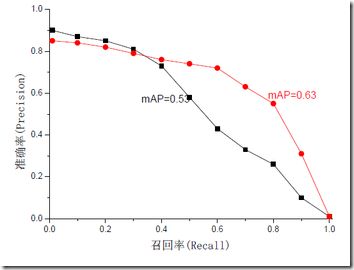
（5）平均准确率MAP（Mean Average Precision）：实际上指的是Precision-recall曲线围成的面积，解决了precision，recall和F-measure的单点局限性。

（6）交并比 IOU（intersection over union）：交比并 

 

使用Python代码画图计算：

1. 计算 召回率（recall）、精准率（precision）和F1-score

 1 from sklearn.metrics import accuracy_score, precision_score, recall_score,f1_score

 2 y_true = [1,1,1,0,0,0,1]
 3 y_pred = [0,1,1,0,1,0,0]
 4 precision = precision_score(y_true, y_pred)
 5 recall = recall_score(y_true, y_pred)
 6 accuracy = accuracy_score(y_true, y_pred)
 7 F1_Score = f1_score(y_true, y_pred)

 8 print("precision = {}".format(precision))
 9 print("recall = {}".format(recall))
10 print("accuracy = {}".format(accuracy))
11 print("F1-score = {}".format(F1_Score))

结果显示：
　　precision = 0.6666666666666666
　　recall = 0.5
　　accuracy = 0.5714285714285714
　　F1-score = 0.5714285714285715

2. 画ROC曲线并计算AUC值

 1 from sklearn.datasets import make_classification
 2 from sklearn.linear_model import LogisticRegression
 3 from sklearn.cross_validation import train_test_split
 4 from sklearn.metrics import roc_auc_score, roc_curve
 5 import matplotlib.pyplot as plt
 6 
 7 # 生成分类数据（X,y）
 8 X, y = make_classification(n_samples=10000, n_features=10,
 9                             n_classes=2,n_informative=5)
10 # 划分训练集和测试集
11 X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2, random_state=0)
12 
13 # 创建logistic回归模型
14 clf = LogisticRegression()
15 # 模型填充数据
16 clf.fit(X_train,y_train)
17 # 模型预测数据
18 preds = clf.predict_proba(X_test)[:,1]
19 
20 # 产生fpr,tpr用于画ROC曲线
21 fpr,tpr,_ = roc_curve(y_test, preds)
22 # 计算AUC值
23 roc_auc = roc_auc_score(y_test,preds)
24  
25 
26 # 开始画图
27 plt.figure()
28 lw = 2
29 
30 plt.plot(fpr, tpr, color='orange', 
31           lw=lw, label='ROC_Curve (area = %0.2f)'% roc_auc)
32  
33 plt.plot([0,1],[0,1], color='navy',lw=lw, linestyle='--')
34 plt.xlim([0.0, 1.0])
35 plt.ylim([0.0, 1.05])
36 plt.xlabel('False Positive Rate')
37 plt.ylabel('True Positive Rate')
38 plt.title('Receiver operating characteristic Line')
39 plt.legend(loc='lower right')
40 plt.show()

 

 

参考资料：

• 周志华 《机器学习》
• 万门大学教学视频 《实用数据挖掘与人工智能一月特训班》
• 百度百科关于假设性检验：http://baike.baidu.com/view/1445854.htm
• 关于MAP讲解的博客： https://blog.csdn.net/chengyq116/article/details/81290447