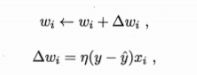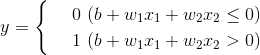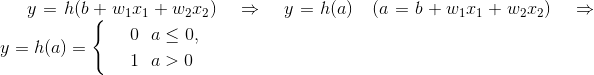感知机与神经元
感知机(Perceptron)由两层神经元组成(输入层、输出层),输入层接收外界输入信号后传递给输出层,输出层是M-P神经元,亦称“阈值逻辑单元”(threshold logic unit)。
输入层只接受输入而没有权重以及阈值,输出层的神经元有阈值,两层间连接有权重。
把阈值当做是第n+1个权重,第n+1个输入是-1,那么就可以把阈值放进权重里了。那么只需要做权重的学习。
根据错误程度进行调整。
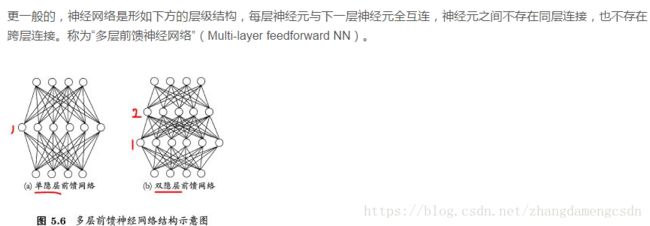
这样两层神经元只能处理线性问题,而非线性问题则需要多层网络。
输入输出层之间的叫做隐层。
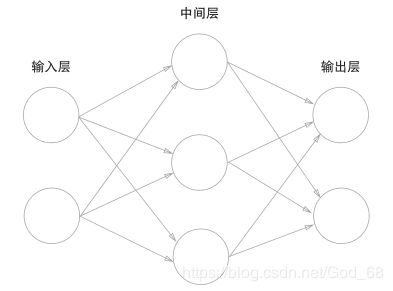
下面主要讲神经网络与感知机的不同之处。首先来看看一个神经网络的示例:
上图示,最左侧是输入层,中间的一列被称为中间层,也被称之为隐藏层,最右一列被称为输出层。
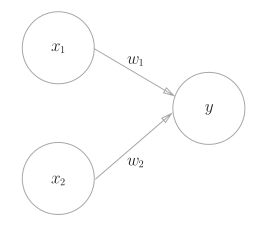
则,神经网络在信号传递的过程中与感知机有什么联系呢?在之前的感知机中提到,其网络结构如下图所示:
公式表示为:
其中,b为偏置,用于控制神经元被激活的容易程度;和 分别表示为各个信号的权重参数,用于控制各个信号的重要性。
现将上述公式改写为:
上式中,输入信号的总和会被函数h(a)转换,转换后的值就是输出 y。然后,所表示的函数h(a),在输入超过0时返回1,否则返回0。
激活函数
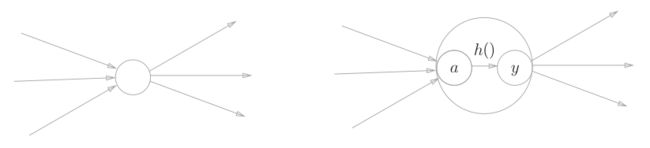
刚才登场的h(a)函数会将输入信号的总和转换为输出信号,这种函数一般称为激活函数(activation function)。如“激活”一词所示,激活函数的作用在于决定如何来激活输入信号的总和。下图右侧,表示神经元的○中明确显示了激活函数的计算过程,即
信号的加权总和为节点 ,然后节点a被激活函数h()转换成节点y。 “神经元”和“节点”两个术语的含义相同。这里,我们称a和y为“节点”,其实它和之前所说的“神经元”含义相同。
左图是一般的神经元的图,右图是在神经元内部明确显示激活函数的计算过程的图(a表示输入信号的总和,h()表示激活函数,y表示输出)
补充:一般而言,“朴素感知机”是指单层网络,指的是激活函数使用了阶跃函数的模型。“多层感知机”是指神经网络,即使用sigmoid函数(后述)等平滑的激活函数的多层网络。