图像平滑去噪之高斯滤波器

　　高斯滤波器是根据高斯函数来选择权值的线性平滑滤波器，对随机分布和服从正态分布的噪声有很好地滤除效果。它可以辅助大部分的边缘检测算法，

对图像的边缘进行扩展（边缘厚度变大），使噪声点的灰度降低，从而减少边缘检测中噪声的数量。

　　二维的高斯函数公式如下：　　　　　　　　　　　　

　　

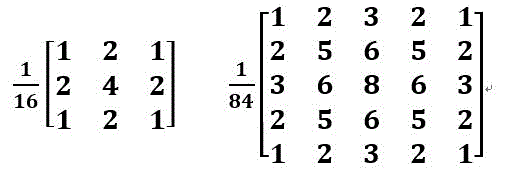
　　其中σ为正态分布的标准偏差，其值决定了高斯函数的变化幅度，对应就是滤波器的权值。高斯函数分布与二维滤波器常见模板如下：

　　       　　

　　模板的生成，就是将矩阵中心作为（0,0）点然后分别代入公式中，求得一个类型为小数的矩阵，将矩阵左上角的元素乘以它的倒数K，使其值为1，

矩阵其他位置的元素也都乘以K，再将矩阵化为整数形式。由此便可以得到一个模板，模板是行列长度为奇数的方阵，取值由σ决定。σ越大，矩阵从里

到外的梯度更大。一般地，按照上面公式所计算的3*3模板的σ=0.85，5*5模板的σ=1.4，7*7模板的σ=1.72。一般根据具体图像情况，选择合适的模板大

小（模糊半径）与标准差（权值），例如目标边缘相距较近时应选用小模板，如果滤波程度不够，σ值可以稍微取大；如果目标呈块状分布，噪点面

积大时可以选用大模板，但整体图像就会变得较模糊。

　　高斯模板卷积图像：高斯模板的卷积是可分离的（矩阵秩=1），因此大小为n*n去卷积m*m大小的图像时，复杂度可以从n²*m²降至2n*m²。这意味

着在相同实时性要求下，可以使用更大的模糊半径。所谓可分离，指将n*n的矩阵拆分成两个大小为n的行向量与列向量，与图像做两次卷积，而卷积结果

与一次卷积相同。

　　下面展示了高斯模糊的一个实例：

　　

　　

　　以下是matlab实现高斯滤波器的代码：

　　

%高斯滤波器模板生成
function template=gaussiantemplate(sigma,size)
    %sigma=0.85 size=3;
    %sigma=1.4 size=5;
    %sigma=1.72 size=7
    syms x y;
    gaussian=(1/(2*pi*sigma^2))*exp((-(x^2+y^2)/(2*sigma^2)));
    template=zeros(size,size);%奇数个
    for i=1:size
        for j=1:size
            template(i,j)=double(subs(gaussian,[x,y],[i-(size+1)/2,j-(size+1)/2]));
        end
    end
    
    k=1/template(1,1);
    for i=1:size
        for j=1:size
            template(i,j)=uint8(template(i,j)*k);
        end
    end
    
    
end　　

%高斯滤波
function gaussian=gaussianfilter(grayimg,sigma,size)
    operator=gaussiantemplate(sigma,size);
    gaussian = filter2(operator,grayimg);
    gaussian = uint8(gaussian./sum(sum(operator)));
end