jdzhangxin
jdzhangxin

高级数据结构和算法4：BST(二叉搜索树)、AVL树(平衡二叉树)

visualgo.net BST AVL

1. 二叉查找树

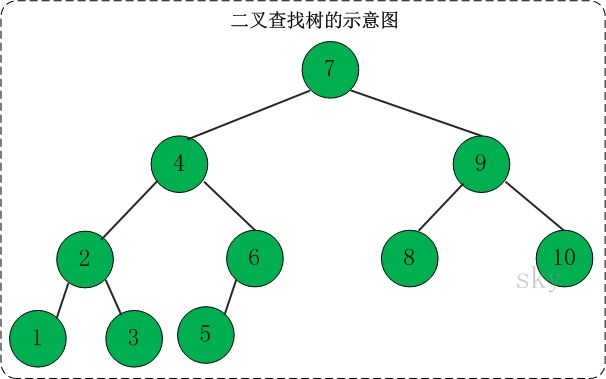
二叉查找树(Binary Search Tree)，又被称为二叉搜索树


高级数据结构和算法4：BST(二叉搜索树)、AVL树(平衡二叉树)_第1张图片

1. 特点

  1. 任意节点的左子树不空, 则左子树上所有节点的key均小于它的根节点的key
  2. 任意节点的右子树不空, 则右子树上所有节点的key均大于它的根节点的key
  3. 任意节点的左,右子树也分别为二叉查找树
  4. 没有key相等的节点

二叉查找树进行中序遍历，可以得到一个递增的有序序列


高级数据结构和算法4：BST(二叉搜索树)、AVL树(平衡二叉树)_第2张图片
BST的中序遍历

2. 结构

二叉搜索树通常使用链式存储孩子表示法。

struct Node {
    int key;
    struct Node* left;
    struct Node* right;
}

3. 操作

3.1 插入

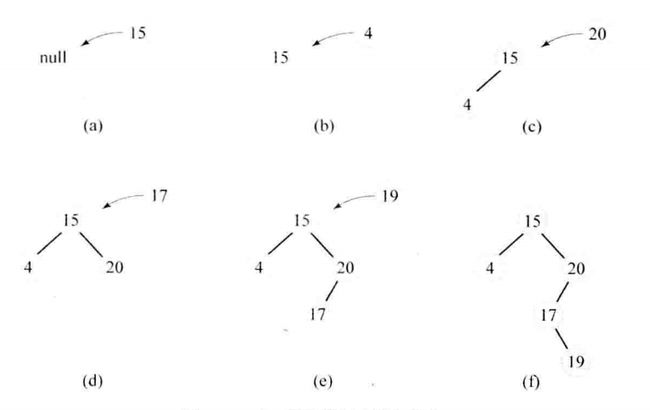
  1. 如果二叉查找树为空，则直接插入。
  2. 如果插入节点key小于根结点key，则插入到左子树中；大于根结点key，则插入到右子树中。
  3. 依次类推，直到找到插入位置。

BST默认插入新的节点是叶子节点。

高级数据结构和算法4：BST(二叉搜索树)、AVL树(平衡二叉树)_第3张图片 
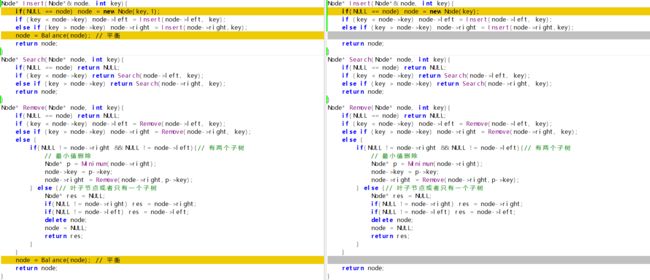
Node* Insert(Node*& node, int key){
    if(NULL == node) node = new Node(key);
    if (key < node->key) node->left = Insert(node->left, key);
    else if (key > node->key) node->right = Insert(node->right,key);    
    return node;
}

3.2 查找

  1. 查找指定key的节点
    从根结点开始，若二叉树非空，将给定值与根结点的关键字比较，若相等，则查找成功；若不等，则当给定值小于根结点关键字时，在根结点的左子树中查找，否则在根结点的右子树中查找。 
    Node* Search(Node* node, int key){
    if(NULL == node) return NULL;
    if (key < node->key) return Search(node->left, key);
    else if (key > node->key) return Search(node->right, key);
    return node;
}
  2. 查找最大/最小key的节点 
    // 最大键
Node* Maximum(Node* node){
    if (NULL == node) return NULL;
    while (NULL != node->right) node = node->right;
    return node;
}

// 最小键
Node* Minimum(Node* node){
    if (NULL == node) return NULL;
    while (NULL != node->left) node = node->left;
    return node;
}

3.3 删除

二叉查找树的删除操作是相对复杂一点，它要按 3 种情况来处理：

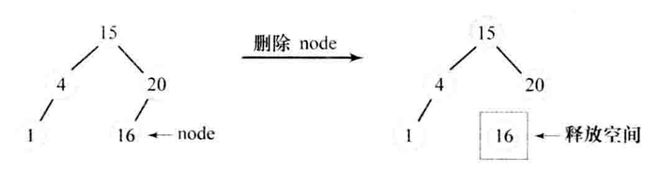
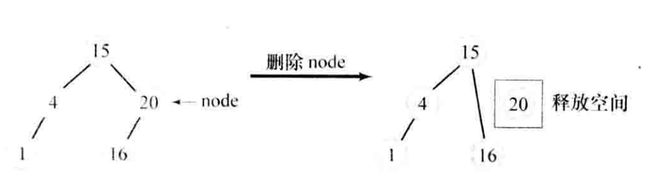
  1. 被删除结点是叶子结点，直接删除。


    高级数据结构和算法4：BST(二叉搜索树)、AVL树(平衡二叉树)_第4张图片

  2. 结点只有左子树或只有右子树，则让子树替代；


    高级数据结构和算法4：BST(二叉搜索树)、AVL树(平衡二叉树)_第5张图片

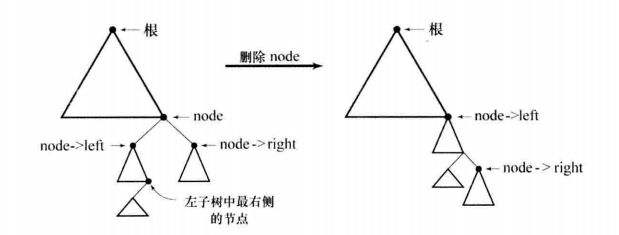
  3. 结点既有左子树，又有右子树，有两种处理方式
    替代删除，后继代替删除节点，然后删除后继；或者前驱代替删除节点，然后删除前驱。
    合并删除，右子树合并到左子树的最大值的右子树上；或者左子树合并到右子树最小值的左子树上。


    高级数据结构和算法4：BST(二叉搜索树)、AVL树(平衡二叉树)_第6张图片
    合并删除-增加树高.png 
Node* Remove(Node* node, int key){
    if(NULL == node) return NULL;
    if (key < node->key) node->left = Remove(node->left, key);
    else if (key > node->key) node->right = Remove(node->right, key);
    else {
        if(NULL != node->right && NULL != node->left){// 有两个子树
            // 最小值删除
            Node* p = Minimum(node->right);
            node->key = p->key;
            node->right = Remove(node->right,p->key);
        } else {// 叶子节点或者只有一个子树
            Node* res = NULL;
            if(NULL != node->right) res = node->right;
            if(NULL != node->left) res = node->left;
            delete node;
            node = NULL;
            return res;
        }
    }
    return node;
}

优缺点

  1. 优点
No. 操作 时间复杂度
1 插入 O(log n)
2 查找 O(log n)
3 插入 O(log n)
  1. 缺点
    二叉搜索树构造顺序影响操作的时间复杂度。

参考代码

#include 
#include 
using namespace std;

// 节点
struct Node{
    int key;        ///< 键
    Node *left;     ///< 左子节点
    Node *right;    ///< 右子节点
    Node(int key) 
    :key(key),left(NULL),right(NULL){}
};

// 辅助操作
Node* Maximum(Node* node){
    if (NULL == node) return NULL;
    while (NULL != node->right) node = node->right;
    return node;
}
Node* Minimum(Node* node){
    if (NULL == node) return NULL;
    while (NULL != node->left) node = node->left;
    return node;
}

// 核心操作
Node* Insert(Node*& node, int key){
    if(NULL == node) node = new Node(key);
    if (key < node->key) node->left = Insert(node->left, key);
    else if (key > node->key) node->right = Insert(node->right,key);    
    return node;
}

Node* Search(Node* node, int key){
    if(NULL == node) return NULL;
    if (key < node->key) return Search(node->left, key);
    else if (key > node->key) return Search(node->right, key);
    return node;
}
Node* Remove(Node* node, int key){
    if(NULL == node) return NULL;
    if (key < node->key) node->left = Remove(node->left, key);
    else if (key > node->key) node->right = Remove(node->right, key);
    else {
        if(NULL != node->right && NULL != node->left){// 有两个子树
            // 最小值删除
            Node* p = Minimum(node->right);
            node->key = p->key;
            node->right = Remove(node->right,p->key);
        } else {// 叶子节点或者只有一个子树
            Node* res = NULL;
            if(NULL != node->right) res = node->right;
            if(NULL != node->left) res = node->left;
            delete node;
            node = NULL;
            return res;
        }
    }
    return node;
}

/////////////////////////////////////////////////////////////
ostream& operator<<(ostream& os,const Node root) {
    queue q;
    q.push(&root);
    while(!q.empty()){
        const Node* curr = q.front();
        q.pop();
        if (NULL != curr){
            os << curr->key;
            q.push(curr->left);
            q.push(curr->right);
        } else {
            os << '#';
        }
    }
    return os;        
}
void TestInsert(Node*& root){
    Insert(root,1);
    Insert(root,2);
    Insert(root,3);
    Insert(root,4);
    Insert(root,5);
    cout << *root << endl;
}
void TestSearch(Node* root,int key){
    cout <<"Search " << key << ":" << Search(root,key) << endl;
}
void TestRemove(Node*& root,int key){
    root = Remove(root, key);
    cout <<"Remove " << key << ":" ;
    if(NULL != root) cout << *root << endl;
    else cout << "#" << endl;
}
void TestMax(Node* root){
    Node* maxNode = Maximum(root);
    cout << "Max:"<< maxNode->key <<":"<< maxNode <key <<":"<< minNode <

2. AVL树(平衡二叉树)

BST树的缺点不平衡


高级数据结构和算法4：BST(二叉搜索树)、AVL树(平衡二叉树)_第7张图片
二叉树的平衡.png

平衡二叉树/自平衡二叉查找树(Balanced Binary Tree)： 也称为AVL树(名称来自发明人G.M. Adelson-Velsky 和 E.M. Landis的首字母)，它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

高级数据结构和算法4：BST(二叉搜索树)、AVL树(平衡二叉树)_第8张图片

特点

  1. 左右子树深度之差的绝对值不超过1(任意节点的两子树的高度最大差别为1).
  2. 左右子树仍然为平衡二叉树.
  • 平衡因子BF(Balance Factor)：左树深度减去右树深度的值。平衡因子BF = 左子树深度－右子树深度。
  • 平衡二叉树每个结点的平衡因子只能是1，0，-1。若其绝对值超过1，则该二叉排序树就是不平衡的。当BF为-1、0、1时，二叉树平衡；反之，不平衡。

树快速查找的关键是高度要低，高度低的关键是平衡。

判断平衡:BF


高级数据结构和算法4：BST(二叉搜索树)、AVL树(平衡二叉树)_第9张图片
判断平衡二叉树 
/* 节点 */
struct Node{
    char key;       // 键值
    Node* right;    // 右节点
    Node* left;     // 左节点
    int height;     // 节点高度
    Node(char key):key(key),right(NULL),left(NULL),height(0){}
    Node(char key,int height):key(key),right(NULL),left(NULL),height(height){}
};

/*
* 平衡因子:左子树树高-右子树树高
*/
int BalanceFactor(const Node* root){
    if(NULL == root) return 0;
    if(NULL == root->left && NULL == root->right) return 0;
    if(NULL == root->left) return -root->right->height;
    if(NULL == root->right) return root->left->height;
    return root->left->height - root->right->height;
}

ostream& operator<<(ostream& os,const Node root) {
    queue q;
    q.push(&root);
    while(!q.empty()){
        const Node* curr = q.front();
        q.pop();
        if (NULL != curr){
            os << curr->key << "[" << BalanceFactor(curr)<<"]";
            q.push(curr->left);
            q.push(curr->right);
        } else {
            os << '#';
        }
    }
    return os;        
}
int main(){
    {
        //     1
        //    /
        //   2
        //  /
        // 3
        Node a('1',3);
        Node b('2',2);
        Node c('3',1);
        a.left = &b;
        b.left = &c;
        cout << a << endl;
    }
    {
        // 1
        //  \
        //   2
        //    \
        //     3
        Node a('1',3);
        Node b('2',2);
        Node c('3',1);
        a.right = &b;
        b.right = &c;
        cout << a << endl;
    }
    {
        //     1
        //    /
        //   2
        //    \
        //     3
        Node a('1', 3);
        Node b('2', 2);
        Node c('3', 1);
        a.left = &b;
        b.right = &c;
        cout << a << endl;
    }
    {
        // 1
        //  \
        //   2
        //  /
        // 3
        Node a('1', 3);
        Node b('2', 2);
        Node c('3', 1);
        a.right = &b;
        b.left = &c;
        cout << a << endl;
    }
}

LeetCode 110. 平衡二叉树

两种旋转(左旋/右旋)、三个节点(新插入节点/不平衡节点/旋转节点)、四种不平衡(LL/RR/RL/LR)。

操作

AVL树的操作基本和二叉查找树一样，这里我们关注的是两个变化很大的操作：插入和删除！

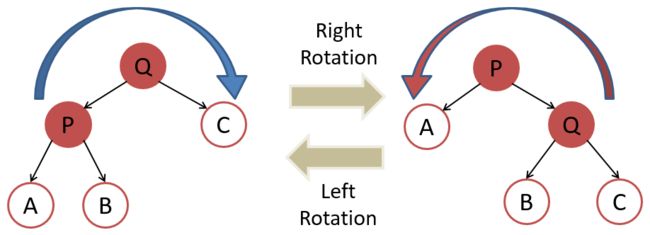
旋转

旋转条件：当最小不平衡子树根节点BF>1,右旋；BF<-1,左旋。


高级数据结构和算法4：BST(二叉搜索树)、AVL树(平衡二叉树)_第10张图片

旋转步骤：

  1. 获取旋转节点
  2. 旋转节点的子节点替换父节点的旋转节点
  3. 旋转节点父节点做旋转节点子节点
  4. 返回旋转节点
#include 
#include 
using namespace std;

/* 节点 */
struct Node{
    char key;       // 键值
    Node* right;    // 右节点
    Node* left;     // 左节点
    int height;     // 节点高度
    Node(char key):key(key),right(NULL),left(NULL),height(0){}
};

ostream& operator<<(ostream& os,const Node root) {
    queue q;
    q.push(&root);
    while(!q.empty()){
        const Node* curr = q.front();
        q.pop();
        if (NULL != curr){
            os << curr->key;
            q.push(curr->left);
            q.push(curr->right);
        } else {
            os << '#';
        }
    }
    return os;        
}

/*
 * 右旋
 *       Q                  P 
 *      / \                / \ 
 *     P   C  ------->    A   Q 
 *    / \                /   / \ 
 *   A   B              X'  B   C  
 *
 */
Node* RightRotate(Node* root){
    Node* pivot = root->left;  // 获取旋转节点
    root->left = pivot->right; // 旋转节点的子节点替换父节点的旋转节点
    pivot->right = root;       // 旋转节点父节点做旋转节点子节点
    return pivot;              // 返回旋转节点
}

/*
 * 左旋
 *      P                    Q
 *     / \                  / \ 
 *    A   Q     ----->     P   C 
 *       / \              / \   \ 
 *      B   C            A   B   X'  
 */
Node* LeftRotate(Node* root){
    Node* pivot = root->right; // 获取旋转节点
    root->right = pivot->left; // 旋转节点的子节点替换父节点的旋转节点
    pivot->left = root;        // 旋转节点父节点做旋转节点子节点
    return pivot;              // 返回旋转节点 
}

int main(){
    {
        Node a('1');
        Node b('2');
        Node c('3');
        a.left = &b;
        b.left = &c;
        cout << a << endl;
        cout << *RightRotate(&a) << endl;
    }
    {
        Node a('1');
        Node b('2');
        Node c('3');
        a.right = &b;
        b.right = &c;
        cout << a << endl;
        cout << *LeftRotate(&a) << endl;
    }
    {
        Node q('Q');
        Node p('P');
        Node c('C');
        Node a('A');
        Node b('B');
        q.left = &p;
        q.right = &c;
        p.left = &a;
        p.right = &b;
        cout << q << endl;
        Node* r = RightRotate(&q);
        cout << *r << endl;
        Node *l = LeftRotate(r);
        cout << *l << endl;
    }
}

四种不平衡

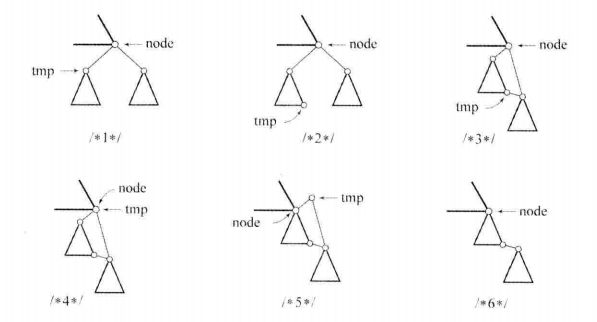
不平衡的四种情况：
LL：插入一个新节点到不平衡节点的左子树（Left）的左子树（Left），导致不平衡节点的平衡因子由1变为2

高级数据结构和算法4：BST(二叉搜索树)、AVL树(平衡二叉树)_第11张图片

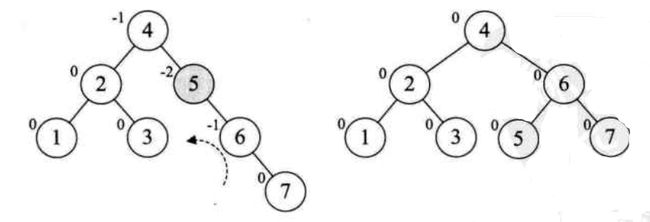
RR：插入一个新节点到不平衡节点的右子树（Right）的右子树（Right），导致不平衡节点的平衡因子由-1变为-2

高级数据结构和算法4：BST(二叉搜索树)、AVL树(平衡二叉树)_第12张图片

LR：插入一个新节点到不平衡节点的左子树（Left）的右子树（Right），导致不平衡节点的平衡因子由1变为2

高级数据结构和算法4：BST(二叉搜索树)、AVL树(平衡二叉树)_第13张图片

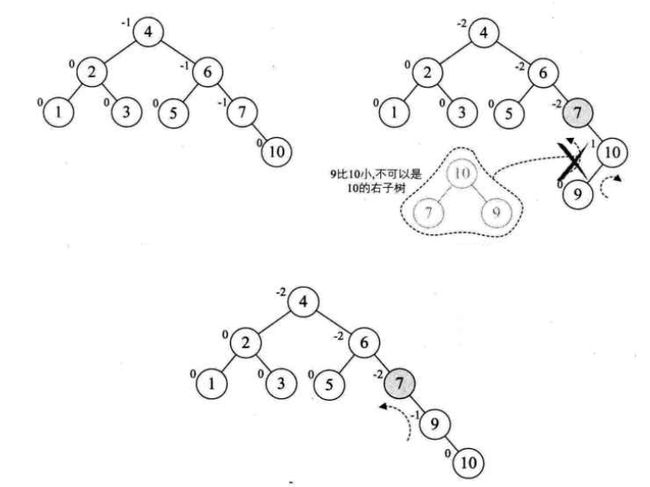
RL：插入一个新节点到不平衡节点的右子树（Right）的左子树（Left），导致不平衡节点的平衡因子由-1变为-2

高级数据结构和算法4：BST(二叉搜索树)、AVL树(平衡二叉树)_第14张图片 
/*
* 检查是否平衡
*/
void Check(Node* root){
    int nf = BalanceFactor(root);
    if(nf>1){
        int lf = BalanceFactor(root->left);
        if(lf > 0) { // LL
            cout << "LL" << endl;
        } else { // LR
            cout << "LR" << endl;
        }
    }else if(nf < -1){
        int rf = BalanceFactor(root->right);
        if (rf < 0) { // RR
            cout << "RR" << endl;
        } else { // RL
            cout << "RL" << endl;
        }
    }else{// 保持平衡的情况
        cout << "Balance" << endl;
    }
}
int main(){
    {
        //     1
        //    /
        //   2
        //  /
        // 3
        Node a('1',3);
        Node b('2',2);
        Node c('3',1);
        a.left = &b;
        b.left = &c;
        cout << a << endl;
        Check(&a);
    }

    {
        // 1
        //  \
        //   2
        //    \
        //     3
        Node a('1',3);
        Node b('2',2);
        Node c('3',1);
        a.right = &b;
        b.right = &c;
        cout << a << endl;
        Check(&a);
    }

    {
        //     1
        //    /
        //   2
        //    \
        //     3
        Node a('1', 3);
        Node b('2', 2);
        Node c('3', 1);
        a.left = &b;
        b.right = &c;
        cout << a << endl;
        Check(&a);
    }

    {
        // 1
        //  \
        //   2
        //  /
        // 3
        Node a('1', 3);
        Node b('2', 2);
        Node c('3', 1);
        a.right = &b;
        b.left = &c;
        cout << a << endl;
        Check(&a);
    }

    {
        //     1
        //    / \
        //   2   4
        //  / \
        // 3   5
        Node a('1', 3);
        Node b('2', 2);
        Node c('3', 1);
        Node d('4', 1);
        Node e('5', 1);
        a.left = &b;
        a.right = &d;
        b.left = &c;
        b.right = &e;
        cout << a << endl;
        Check(&a);
    }

    {
        //   1
        //  / \
        // 4   2
        //    / \
        //   5   3
        Node a('1', 3);
        Node b('2', 2);
        Node c('3', 1);
        Node d('4', 1);
        Node e('5', 1);
        a.right = &b;
        a.left = &d;
        b.right = &c;
        b.left = &e;
        cout << a << endl;
        Check(&a);
    }

    {
        //       1
        //      / \
        //     2   4
        //    / \
        //   3   5
        //  /
        // 6
        Node a('1', 4);
        Node b('2', 3);
        Node c('3', 2);
        Node d('4', 1);
        Node e('5', 1);
        Node f('6', 1);
        a.left = &b;
        a.right = &d;
        b.left = &c;
        b.right = &e;
        c.left = &f;
        cout << a << endl;
        Check(&a);
    }

    {
        //       1
        //      / \
        //     2   4
        //    / \
        //   3   5
        //    \
        //     6
        Node a('1', 4);
        Node b('2', 3);
        Node c('3', 2);
        Node d('4', 1);
        Node e('5', 1);
        Node f('6', 1);
        a.left = &b;
        a.right = &d;
        b.left = &c;
        b.right = &e;
        c.right = &f;
        cout << a << endl;
        Check(&a);
    }

    {
        //       1
        //      / \
        //     2   4
        //    / \
        //   3   5
        //      /
        //     6
        Node a('1', 4);
        Node b('2', 3);
        Node c('3', 1);
        Node d('4', 1);
        Node e('5', 2);
        Node f('6', 1);
        a.left = &b;
        a.right = &d;
        b.left = &c;
        b.right = &e;
        e.left = &f;
        cout << a << endl;
        Check(&a);
    }

    {
        //       1
        //      / \
        //     2   4
        //    / \
        //   3   5
        //        \
        //         6
        Node a('1', 4);
        Node b('2', 3);
        Node c('3', 1);
        Node d('4', 1);
        Node e('5', 2);
        Node f('6', 1);
        a.left = &b;
        a.right = &d;
        b.left = &c;
        b.right = &e;
        e.right = &f;
        cout << a << endl;
        Check(&a);
    }

    {
        //   1
        //  / \
        // 4   2
        //    / \
        //   5   3
        //  /
        // 6
        Node a('1', 3);
        Node b('2', 2);
        Node c('3', 1);
        Node d('4', 1);
        Node e('5', 1);
        Node f('6', 1);
        a.right = &b;
        a.left = &d;
        b.right = &c;
        b.left = &e;
        e.left = &f;
        cout << a << endl;
        Check(&a);
    }
}

不平衡处理方法

  • 单向右旋平衡处理LL
  • 单向左旋平衡处理RR
  • 双向旋转（先左后右）平衡处理LR
  • 双向旋转（先右后左）平衡处理RL
高级数据结构和算法4：BST(二叉搜索树)、AVL树(平衡二叉树)_第15张图片
image.png 
/*
* 平衡
*/
Node* Balance(Node* root){
    Node *res = root;
    int nf = BalanceFactor(root);
    if(nf>1){
        int lf = BalanceFactor(root->left);
        if(lf > 0) { // LL
            cout << "LL" << endl;
            res = RightRotate(root);
        } else { // LR
            cout << "LR" << endl;
            root->left = LeftRotate(root->left);
            res = RightRotate(root);
        }
    }else if(nf <-1){
        int rf = BalanceFactor(root->right);
        if (rf < 0) { // RR
            cout << "RR" << endl;
            res = LeftRotate(root);
        } else { // RL
            cout << "RL" << endl;
            root->right = RightRotate(root->right);
            res = LeftRotate(root);
        }
    }else{
        cout << "Balance" << endl;
        // 保持平衡的情况
    }
    return res;
}
int main(){
    {
        //     1
        //    /
        //   2
        //  /
        // 3
        Node a('1',3);
        Node b('2',2);
        Node c('3',1);
        a.left = &b;
        b.left = &c;
        cout << a << endl;
        Check(&a);
        cout << *Balance(&a) << endl;
        cout << "----------------" << endl;
    }

    {
        // 1
        //  \
        //   2
        //    \
        //     3
        Node a('1',3);
        Node b('2',2);
        Node c('3',1);
        a.right = &b;
        b.right = &c;
        cout << a << endl;
        Check(&a);
        cout << *Balance(&a) << endl;
        cout << "----------------" << endl;
    }

    {
        //     1
        //    /
        //   2
        //    \
        //     3
        Node a('1', 3);
        Node b('2', 2);
        Node c('3', 1);
        a.left = &b;
        b.right = &c;
        cout << a << endl;
        Check(&a);
        cout << *Balance(&a) << endl;
        cout << "----------------" << endl;
    }

    {
        // 1
        //  \
        //   2
        //  /
        // 3
        Node a('1', 3);
        Node b('2', 2);
        Node c('3', 1);
        a.right = &b;
        b.left = &c;
        cout << a << endl;
        Check(&a);
        cout << *Balance(&a) << endl;
        cout << "----------------" << endl;
    }

    {
        //     1
        //    / \
        //   2   4
        //  / \
        // 3   5
        Node a('1', 3);
        Node b('2', 2);
        Node c('3', 1);
        Node d('4', 1);
        Node e('5', 1);
        a.left = &b;
        a.right = &d;
        b.left = &c;
        b.right = &e;
        cout << a << endl;
        Check(&a);
        cout << *Balance(&a) << endl;
        cout << "----------------" << endl;
    }

    {
        //   1
        //  / \
        // 4   2
        //    / \
        //   5   3
        Node a('1', 3);
        Node b('2', 2);
        Node c('3', 1);
        Node d('4', 1);
        Node e('5', 1);
        a.right = &b;
        a.left = &d;
        b.right = &c;
        b.left = &e;
        cout << a << endl;
        Check(&a);
        cout << *Balance(&a) << endl;
        cout << "----------------" << endl;
    }

    {
        //       1
        //      / \
        //     2   4
        //    / \
        //   3   5
        //  /
        // 6
        Node a('1', 4);
        Node b('2', 3);
        Node c('3', 2);
        Node d('4', 1);
        Node e('5', 1);
        Node f('6', 1);
        a.left = &b;
        a.right = &d;
        b.left = &c;
        b.right = &e;
        c.left = &f;
        cout << a << endl;
        Check(&a);
        cout << *Balance(&a) << endl;
        cout << "----------------" << endl;
    }

    {
        //       1
        //      / \
        //     2   4
        //    / \
        //   3   5
        //    \
        //     6
        Node a('1', 4);
        Node b('2', 3);
        Node c('3', 2);
        Node d('4', 1);
        Node e('5', 1);
        Node f('6', 1);
        a.left = &b;
        a.right = &d;
        b.left = &c;
        b.right = &e;
        c.right = &f;
        cout << a << endl;
        Check(&a);
        cout << *Balance(&a) << endl;
        cout << "----------------" << endl;
    }

    {
        //       1
        //      / \
        //     2   4
        //    / \
        //   3   5
        //      /
        //     6
        Node a('1', 4);
        Node b('2', 3);
        Node c('3', 1);
        Node d('4', 1);
        Node e('5', 2);
        Node f('6', 1);
        a.left = &b;
        a.right = &d;
        b.left = &c;
        b.right = &e;
        e.left = &f;
        cout << a << endl;
        Check(&a);
        cout << *Balance(&a) << endl;
        cout << "----------------" << endl;
    }

    {
        //       1
        //      / \
        //     2   4
        //    / \
        //   3   5
        //        \
        //         6
        Node a('1', 4);
        Node b('2', 3);
        Node c('3', 1);
        Node d('4', 1);
        Node e('5', 2);
        Node f('6', 1);
        a.left = &b;
        a.right = &d;
        b.left = &c;
        b.right = &e;
        e.right = &f;
        cout << a << endl;
        Check(&a);
        cout << *Balance(&a) << endl;
        cout << "----------------" << endl;
    }
}

更新树高

/*
* 更新树高
*/
int UpdateHeight(Node* root){
    if(NULL == root) return 0;
    if(NULL == root->left && NULL == root->right) {
        root->height = 1;
    } else if(NULL == root->left) {
        root->height = 1 + UpdateHeight(root->right);
    } else if(NULL == root->right) {
        root->height = 1 + UpdateHeight(root->left);
    } else {
        root->height = 1 + max(UpdateHeight(root->left),UpdateHeight(root->right));
    }
    return root->height;
}

插入

与 BST（二叉搜索树）中类似，先进行一次失败的查找来确定插入的位置，插入节点后根据平衡因子来决定是否需要调整。

高级数据结构和算法4：BST(二叉搜索树)、AVL树(平衡二叉树)_第16张图片
二叉树的平衡1-右旋.png

高级数据结构和算法4：BST(二叉搜索树)、AVL树(平衡二叉树)_第17张图片
二叉树的平衡2-左旋.png

高级数据结构和算法4：BST(二叉搜索树)、AVL树(平衡二叉树)_第18张图片
二叉树的平衡3-左旋.png

高级数据结构和算法4：BST(二叉搜索树)、AVL树(平衡二叉树)_第19张图片
二叉树的平衡4-左旋.png

高级数据结构和算法4：BST(二叉搜索树)、AVL树(平衡二叉树)_第20张图片
二叉树的平衡5-右旋左旋.png

高级数据结构和算法4：BST(二叉搜索树)、AVL树(平衡二叉树)_第21张图片
二叉树的平衡6-右旋左旋.png 
/*
* 插入AVL树
*/
bool Insert(Node*& root,char key){
    bool res;
    if (NULL == root){
        root = new Node(key);
        res = true;
    } else if (root->key == key){
        res = false;
    } else if (root->key < key){
        res = Insert(root->right, key);
    } else {
        res = Insert(root->left, key);
    }
    if(res){
        root = Balance(root);
        UpdateHeight(root); // 更新高度
    }
    return res;
}

删除

删除和 BST 类似，将结点与后继交换后再删除。
删除会导致树高以及平衡因子变化，这时需要沿着被删除结点到根的路径来调整这种变化。

高级数据结构和算法4：BST(二叉搜索树)、AVL树(平衡二叉树)_第22张图片
复制删除.png
高级数据结构和算法4：BST(二叉搜索树)、AVL树(平衡二叉树)_第23张图片
合并删除.png
高级数据结构和算法4：BST(二叉搜索树)、AVL树(平衡二叉树)_第24张图片
合并删除2.png

优点

查找、插入和删除在平均和最坏情况下都是O(logn)。

缺点

插入和删除旋转比较耗时，适用于插入和删除较少的情况。

参考代码

#include 
#include 
using namespace std;

struct Node{
    int key;        ///< 键
    Node *left;     ///< 左子节点
    Node *right;    ///< 右子节点
    int height;     ///< 节点高度
    Node(int key, int height) 
    :key(key),left(NULL),right(NULL),height(height){}
};

// 辅助操作
Node* Maximum(Node* node){
    if (NULL == node) return NULL;
    while (NULL != node->right) node = node->right;
    return node;
}

Node* Minimum(Node* node){
    if (NULL == node) return NULL;
    while (NULL != node->left) node = node->left;
    return node;
}

// 平衡因子:左子树树高-右子树树高
int BalanceFactor(const Node* root){
    if(NULL == root) return 0;
    if(NULL == root->left && NULL == root->right) return 0;
    if(NULL == root->left) return -root->right->height;
    if(NULL == root->right) return root->left->height;
    return root->left->height - root->right->height;
}

/*
 * 右旋
 *       Q                  P 
 *      / \                / \ 
 *     P   C  ------->    A   Q 
 *    / \                /   / \ 
 *   A   B              X'  B   C  
 *
 */
Node* RightRotate(Node* root){
    Node* pivot = root->left;  // 获取旋转节点
    root->left = pivot->right; // 旋转节点的子节点替换父节点的旋转节点
    pivot->right = root;       // 旋转节点父节点做旋转节点子节点
    return pivot;              // 返回旋转节点
}

/*
 * 左旋
 *      P                    Q
 *     / \                  / \ 
 *    A   Q     ----->     P   C 
 *       / \              / \   \ 
 *      B   C            A   B   X'  
 */
Node* LeftRotate(Node* root){
    Node* pivot = root->right; // 获取旋转节点
    root->right = pivot->left; // 旋转节点的子节点替换父节点的旋转节点
    pivot->left = root;        // 旋转节点父节点做旋转节点子节点
    return pivot;              // 返回旋转节点 
}

// 更新树高
int UpdateHeight(Node* root){
    if(NULL == root) return 0;
    if(NULL == root->left && NULL == root->right) {
        root->height = 1;
    } else if(NULL == root->left) {
        root->height = 1 + UpdateHeight(root->right);
    } else if(NULL == root->right) {
        root->height = 1 + UpdateHeight(root->left);
    } else {
        root->height = 1 + max(UpdateHeight(root->left),UpdateHeight(root->right));
    }
    return root->height;
}

// 平衡
Node* Balance(Node* root){
    Node *res = root;
    int nf = BalanceFactor(root);
    if(nf>1){
        int lf = BalanceFactor(root->left);
        if(lf > 0) { // LL
            cout << "LL" << endl;
            res = RightRotate(root);
        } else { // LR
            cout << "LR" << endl;
            root->left = LeftRotate(root->left);
            res = RightRotate(root);
        }
    }else if(nf <-1){
        int rf = BalanceFactor(root->right);
        if (rf < 0) { // RR
            cout << "RR" << endl;
            res = LeftRotate(root);
        } else { // RL
            cout << "RL" << endl;
            root->right = RightRotate(root->right);
            res = LeftRotate(root);
        }
    }else{
        cout << "Balance" << endl;
        // 保持平衡的情况
        // return res;
    }
    UpdateHeight(res);
    return res;
}

// 三个核心操作
Node* Insert(Node* node, int key){
    if(NULL == node) node = new Node(key,1);
    if (key < node->key) node->left = Insert(node->left, key);
    else if (key > node->key) node->right = Insert(node->right,key);
    node = Balance(node); // 平衡
    return node;
}

Node* Search(Node* node, int key){
    if(NULL == node) return NULL;
    if (key < node->key) return Search(node->left, key);
    else if (key > node->key) return Search(node->right, key);
    return node;
}

Node* Remove(Node* node, int key){
    if(NULL == node) return NULL;
    if (key < node->key) node->left = Remove(node->left, key);
    else if (key > node->key) node->right = Remove(node->right, key);
    else {
        if(NULL != node->right && NULL != node->left){// 有两个子树
            // 最小值删除
            Node* p = Minimum(node->right);
            node->key = p->key;
            node->right = Remove(node->right,p->key);
        } else {// 叶子节点或者只有一个子树
            Node* res = NULL;
            if(NULL != node->right) res = node->right;
            if(NULL != node->left) res = node->left;
            delete node;
            node = NULL;
            return res;
        }
    }
    node = Balance(node); // 平衡
    return node;
}
/////////////////////////////////////////////////////////////
ostream& operator<<(ostream& os,const Node root) {
    queue q;
    q.push(&root);
    while(!q.empty()){
        const Node* curr = q.front();
        q.pop();
        if (NULL != curr){
            os << curr->key << '[' << curr->height <<']';
            q.push(curr->left);
            q.push(curr->right);
        } else {
            os << '#';
        }
    }
    return os;        
}
void TestInsert(Node*& root){
    root = Insert(root,1);
    root = Insert(root,2);
    root = Insert(root,3);
    root = Insert(root,4);
    root = Insert(root,5);
    cout << *root << endl;
}
void TestSearch(Node* root,int key){
    cout <<"Search " << key << ":" << Search(root,key) << endl;
}
void TestRemove(Node*& root,int key){
    root = Remove(root, key);
    cout <<"Remove " << key << ":" ;
    if(NULL != root) cout << *root << endl;
    else cout << "#" << endl;
}
void TestMax(Node* root){
    Node* maxNode = Maximum(root);
    cout << "Max:"<< maxNode->key <<":"<< maxNode <key <<":"<< minNode <

BST与AVL比较

高级数据结构和算法4：BST(二叉搜索树)、AVL树(平衡二叉树)_第25张图片

你可能感兴趣的:(高级数据结构和算法4：BST(二叉搜索树)、AVL树(平衡二叉树))

  • 底层逆袭到底有多难，不甘平凡的你准备好了吗？让吴起给你说说 造命者说
    底层逆袭到底有多难，不甘平凡的你准备好了吗？让吴起给你说说我叫吴起，生于公元前440年的战国初期，正是群雄并起、天下纷争不断的时候。后人说我是军事家、政治家、改革家，是兵家代表人物。评价我一生历仕鲁、魏、楚三国，通晓兵家、法家、儒家三家思想，在内政军事上都有极高的成就。周安王二十一年（公元前381年），因变法得罪守旧贵族，被人乱箭射死。我出生在卫国一个“家累万金”的富有家庭，从年轻时候起就不甘平凡
  • 2020-01-25 晴岚85
    郑海燕坚持分享590天2020.1.24在生活中只存在两个问题。一个问题是：你知道想要达成的目标是什么，但却不知道如何才能达成；另一个问题是：你不知道你的目标是什么。前一个是行动的问题，后一个是结果的问题。通过制定具体的下一步行动，可以解决不知道如何开始行动的问题。而通过去想象结果，对结果做预估，可以解决找不着目标的问题。对于所有吸引我们注意力，想要完成的任务，你可以先想象一下，预期的结果究竟是什
  • 谢谢你们，爱你们！ 鹿游儿
    昨天家人去泡温泉，二个孩子也带着去，出发前一晚，匆匆下班，赶回家和孩子一起收拾。饭后，我拿出笔和本子（上次去澳门时做手帐的本子）写下了1\2\3\4\5\6\7\8\9,让后让小壹去思考，带什么出发去旅游呢？她在对应的数字旁边画上了，泳衣、泳圈、肖恩、内衣内裤、tapuy、拖鞋……画完后，就让她自己对着这个本子，将要带的，一一带上，没想到这次带的书还是这本《便便工厂》(晚上姑婆发照片过来，妹妹累得
  • 《投行人生》读书笔记 小蘑菇的树洞
    《投行人生》----作者詹姆斯-A-朗德摩根斯坦利副主席40年的职业洞见-很短小精悍的篇幅，比较适合初入职场的新人。第一部分成功的职业生涯需要规划1.情商归为适应能力分享与协作同理心适应能力，更多的是自我意识，你有能力识别自己的情并分辨这些情绪如何影响你的思想和行为。2.对于初入职场的人的建议，细节，截止日期和数据很重要截止日期，一种有效的方法是请老板为你所有的任务进行优先级排序。和老板喝咖啡的好
  • Long类型前后端数据不一致 igotyback 前端
    响应给前端的数据浏览器控制台中response中看到的Long类型的数据是正常的到前端数据不一致前后端数据类型不匹配是一个常见问题，尤其是当后端使用Java的Long类型（64位）与前端JavaScript的Number类型（最大安全整数为2^53-1，即16位）进行数据交互时，很容易出现精度丢失的问题。这是因为JavaScript中的Number类型无法安全地表示超过16位的整数。为了解决这个问
  • 绘本讲师训练营【24期】8/21阅读原创《独生小孩》 1784e22615e0
    24016-孟娟《独生小孩》图片发自App今天我想分享一个蛮特别的绘本，讲的是一个特殊的群体，我也是属于这个群体，80后的独生小孩。这是一本中国绘本，作者郭婧，也是一个80厚。全书一百多页，均为铅笔绘制，虽然为黑白色调，但并不显得沉闷。全书没有文字，犹如“默片”，但并不影响读者对该作品的理解，反而显得神秘，梦幻，給读者留下想象的空间。作者在前蝴蝶页这样写到：“我更希望父母和孩子一起分享这本书，使他
  • 高级编程--XML+socket练习题 masa010 java开发语言
    1.北京华北2114.8万人上海华东2,500万人广州华南1292.68万人成都华西1417万人（1）使用dom4j将信息存入xml中（2）读取信息，并打印控制台（3）添加一个city节点与子节点（4）使用socketTCP协议编写服务端与客户端，客户端输入城市ID，服务器响应相应城市信息（5）使用socketTCP协议编写服务端与客户端，客户端要求用户输入city对象，服务端接收并使用dom4j
  • 本周第二次约练 2cfbdfe28a51
    中原焦点团队中24初26刘霞2021.12.3约练161次，分享第368天当事人虽然是带着问题来的，但是咨询过程中发现，她是经过自己不断地调整和努力才走到现在的，看到当事人的不容易，找到例外，发现资源，力量感也就随之而来。增强画面感，或者说重温，会给当事人带来更深刻的感受。
  • 今日联对0306 诗图佳得
    自对联：烟销皓月临江浒，水漫金山荡塔裙。一一肖士平2020.3.6.1、试对肖老师联：烟销皓月临江浒，夜笼寒沙梦晚舟。耀哥求正2、试对萧老师联:烟销浩月临江浒，雾散乾坤解汉城。秀霞习作请各位老师校正3、自对联：烟销皓月临江浒，水漫金山荡塔裙。一一肖士平2020.3.6.4、试对肖老师垫场联：烟销皓月临江浒，雾锁寒林缈葉丛。小智求正[抱拳]5、试对肖老师联：烟销皓月临江浒；风卷乱云入峰巅。一一五品6
  • 2022-07-08 保利学府里李楚怡1307022
    ——保利碧桂园学府里——童梦奇趣【科学实验室】「7.9-7.10」✏玩出大智慧约99-144㎡二期全新升级力作
  • 2022-04-18 Apbenz
    语重心长的和我说，不要老是说不行，人至而立之年危机四伏，内在的，外在的，感觉就是心力憔悴，让人无所适从。面对职场的无情，突然好羡慕干体力劳动的外卖小哥。难道命运是想让我去送外卖了吗？干体力活才能让我活下去？fastadmin打卡成功,淘宝金币任务完成。ㅏㅓㅗㅜㅡㅣㅐㅔㅑㅕㅛㅠㅢㅒㅖY行。야자여자요리우유의사얘기예
  • 每日一题——第八十二题 互联网打工人no1 C语言程序设计每日一练c语言
    题目：将一个控制台输入的字符串中的所有元音字母复制到另一字符串中#include#include#include#include#defineMAX_INPUT1024boolisVowel(charp);intmain(){charinput[MAX_INPUT];charoutput[MAX_INPUT];printf("请输入一串字符串：\n");fgets(input,sizeof(inp
  • 每日一题——第八十三题 互联网打工人no1 C语言程序设计每日一练c语言
    题目：将输入的整形数字输出,输出1990，输出"1990"#include#defineMAX_INPUT1024intmain(){intarrr_num[MAX_INPUT];intnum,i=0;printf("请输入一个数字：");scanf_s("%d",&num);while(num!=0){arrr_num[i++]=num%10;num/=10;}printf("\"");for(
  • Python中os.environ基本介绍及使用方法 鹤冲天Pro #Pythonpython服务器开发语言
    文章目录python中os.environos.environ简介os.environ进行环境变量的增删改查python中os.environ的使用详解1.简介2.key字段详解2.1常见key字段3.os.environ.get()用法4.环境变量的增删改查和判断是否存在4.1新增环境变量4.2更新环境变量4.3获取环境变量4.4删除环境变量4.5判断环境变量是否存在python中os.envi
  • 第四天旅游线路预览——从换乘中心到喀纳斯湖 陟彼高冈yu 基于Googleearthstudio的旅游规划和预览旅游
    第四天：从贾登峪到喀纳斯风景区入口，晚上住宿贾登峪；换乘中心有4路车，喀纳斯①号车，去喀纳斯湖，路程时长约5分钟；将上面的的行程安排进行动态展示，具体步骤见”Googleearthstudio进行动态轨迹显示制作过程“、“Googleearthstudio入门教程”和“Googleearthstudio进阶教程“相关内容，得到行程如下所示：Day4-2-480p
  • linux sdl windows.h,Windows下的SDL安装 奔跑吧linux内核 linuxsdlwindows.h
    首先你要下载并安装SDL开发包。如果装在C盘下，路径为C:\SDL1.2.5如果在WINDOWS下。你可以按以下步骤：1.打开VC++，点击"Tools",Options2,点击directories选项3.选择"Includefiles"增加一个新的路径。"C:\SDL1.2.5\include"4，现在选择"Libaryfiles“增加"C:\SDL1.2.5\lib"现在你可以开始编写你的第
  • Goolge earth studio 进阶4——路径修改与平滑 陟彼高冈yu Googleearthstudio进阶教程旅游
    如果我们希望在大约中途时获得更多的城市鸟瞰视角。可以将相机拖动到这里并创建一个新的关键帧。camera_target_clip_7EarthStudio会自动平滑我们的路径，所以当我们通过这个关键帧时，不是一个生硬的角度，而是一个平滑的曲线。camera_target_clip_8路径上有贝塞尔控制手柄，允许我们调整路径的形状。右键单击，我们可以选择“平滑路径”，这是默认的自动平滑算法，或者我们可
  • Python教程：一文了解使用Python处理XPath 旦莫 Python进阶python开发语言
    目录1.环境准备1.1安装lxml1.2验证安装2.XPath基础2.1什么是XPath？2.2XPath语法2.3示例XML文档3.使用lxml解析XML3.1解析XML文档3.2查看解析结果4.XPath查询4.1基本路径查询4.2使用属性查询4.3查询多个节点5.XPath的高级用法5.1使用逻辑运算符5.2使用函数6.实战案例6.1从网页抓取数据6.1.1安装Requests库6.1.2代
  • 相信相信的力量 孙丽_cdb3
    孙丽中级十期坚持分享第345天有一个特别有哲理的故事：有一只老鹰下了蛋，这个蛋，不知怎的就滚到了鸡窝里去了，鸡也下了一窝蛋，然后鸡妈妈把这些蛋全都浮出来了，孵出来之后等小鸡长大一点了，就觉得鹰蛋孵出来的那只小鹰怪模怪样，这些小鸡都嘲笑它，真难看，真笨，丑死了，那只小鹰觉得自己真是谁也不像，真是不好看，后来鸡妈妈也不喜欢他，我怎么生出你这样的孩子来了？真烦人，后来这群小鸡和小鹰一起生活，有一天，老鹰
  • 基于社交网络算法优化的二维最大熵图像分割 智能算法研学社（Jack旭） 智能优化算法应用图像分割算法php开发语言
    智能优化算法应用：基于社交网络优化的二维最大熵图像阈值分割-附代码文章目录智能优化算法应用：基于社交网络优化的二维最大熵图像阈值分割-附代码1.前言2.二维最大熵阈值分割原理3.基于社交网络优化的多阈值分割4.算法结果：5.参考文献：6.Matlab代码摘要：本文介绍基于最大熵的图像分割，并且应用社交网络算法进行阈值寻优。1.前言阅读此文章前，请阅读《图像分割：直方图区域划分及信息统计介绍》htt
  • 509. 斐波那契数(每日一题) lzyprime
    lzyprime博客(github)创建时间：2021.01.04qq及邮箱：2383518170leetcode笔记题目描述斐波那契数，通常用F(n)表示，形成的序列称为斐波那契数列。该数列由0和1开始，后面的每一项数字都是前面两项数字的和。也就是：F(0)=0，F(1)=1F(n)=F(n-1)+F(n-2)，其中n>1给你n，请计算F(n)。示例1：输入：2输出：1解释：F(2)=F(1)+
  • 郎朗大婚娶公主：所有光环的背后，都是十年如一日的自律 简小尘
    近日，关于郎朗大婚的新闻上了热搜，看了新娘的照片，既有天使般的面容，更有魔鬼般的身材，关键是人家还身世好，又有才华，这真的是让所有男人羡慕嫉妒恨哪。有些人不禁会想，“凭什么郎朗的人生就象开挂了一样，可我却每天都活得这么狼狈！”其实，每个开挂的人生背后，都是苦行僧般的自律。01欲戴王冠，必承其重。练琴不能只靠兴趣，更需要自律！我们先来看一下朗朗在小时候的作息时间表：早晨5:45起床，练琴1小时。中午
  • 《中华小厨师》单行VS爱藏：姜是老的辣，书是新的好 cicoky
    《汉书·郦食其传》有曰：“王者以民为天，而民以食为天。”自古以来，吃饱饭是每一个人的基本要求，而吃好饭却是每一个人的最终追求。于是，厨师这一职业孕育而生，其渊源之久，甚至可追溯到4000年前的奴隶时代。职业本身无贵贱，但职业能力却有高低之分。所以一家餐馆生意好不好，厨师的水平决定一切，而站在所有厨师顶端的就被称之为“特级厨师”。今天要说的就是一个关于“特级厨师刘昴星”的故事。连载历程1995年第4
  • 2023-04-17|篮球女孩 长一木
    1小学抑或初中阶段，在课外书了解到她的故事。“篮球女孩”。当时佩服她的顽强，也对生命多了一丝敬畏。今天刚好在公众号看到，长大后的“篮球女孩”。佩服之余又满是心疼。网络侵删祝那素未蒙面的女孩，未来一切顺遂。
  • 高端密码学院笔记285 柚子_b4b4
    高端幸福密码学院（高级班）幸福使者：李华第（598）期《幸福》之回归内在深层生命原动力基础篇——揭秘“激励”成长的喜悦心理案例分析主讲：刘莉一，知识扩充:成功=艰苦劳动+正确方法+少说空话。贪图省力的船夫，目标永远下游。智者的梦再美，也不如愚人实干的脚印。幸福早课堂2020.10.16星期五一笔记:1，重视和珍惜的前提是知道它的价值非常重要，当你珍惜了，你就真正定下来，真正的学到身上。2，大家需要
  • 2020-04-12每天三百字之连接与替代 冷眼看潮
    不知道是不是好为人师，有时候还真想和别人分享一下我对某些现象的看法或者解释。人类社会不断发展进步的过程，就是不断连接与替代的过程。人类发现了火并应用火以后，告别了茹毛饮血的野兽般的原始生活（火烧、烹饪替代了生食）人类用石器代替了完全手工，工具的使用使人类进步一大步。类似这样的替代还有很多，随着科技的发展，有更多的原始的事物被替代，代之以更高效、更先进的技术。在近现代，汽车替代了马车，高速公路和铁路
  • 如何部分格式化提示模板:LangChain中的高级技巧 nseejrukjhad langchainjava服务器python
    标题:如何部分格式化提示模板:LangChain中的高级技巧内容:如何部分格式化提示模板:LangChain中的高级技巧引言在使用大型语言模型(LLM)时,提示工程是一个关键环节。LangChain提供了强大的提示模板功能,让我们能更灵活地构建和管理提示。本文将介绍LangChain中一个高级特性-部分格式化提示模板,这个技巧可以让你的提示管理更加高效和灵活。什么是部分格式化提示模板?部分格式化提
  • 数组去重 好奇的猫猫猫
    整理自js中基础数据结构数组去重问题思考？如何去除数组中重复的项例如数组：[1,3,4,3,5]我们在做去重的时候，一开始想到的肯定是，逐个比较，外面一层循环，内层后一个与前一个一比较，如果是久不将当前这一项放进新的数组，挨个比较完之后返回一个新的去过重复的数组不好的实践方式上述方法效率极低，代码量还多，思考？有没有更好的方法这时候不禁一想当然有了！！！hashtable啊，通过对象的hash办法
  • 春季养肝正当时 dxn悟
    重温快乐2023年2月4日立春。春天来了，春暖花开，小鸟欢唱，那在这样的季节我们如何养肝呢？自然界的春季对应中医五行的木，人体五脏肝属木，“木曰曲直”，是以树干曲曲直直地向上、向外伸长舒展的生发姿态，来形容具有生长、升发、条达、舒畅等特征的食物及现象。根据中医天人相应的理念，肝五行属木，喜条达，主疏泄，与春天相应，所以春天最适合养肝。养肝首先要少生气，因为肝喜条达恶抑郁。人体五志肝为怒，生气发怒最
  • log4j配置 yy爱yy
    #log4j.rootLogger配置的是大于等于当前级别的日志信息的输出#log4j.rootLogger用法:（注意appenderName可以是一个或多个）#log4j.rootLogger=日志级别,appenderName1,appenderName2,....#log4j.appender.appenderName2定义的是日志的输出方式，有两种：一种是命令行输出或者叫控制台输出，另一
  • Enum用法 不懂事的小屁孩 enum
    以前的时候知道enum，但是真心不怎么用，在实际开发中，经常会用到以下代码: protected final static String XJ = "XJ"; protected final static String YHK = "YHK"; protected final static String PQ = "PQ";
  • 【Spark九十七】RDD API之aggregateByKey bit1129 spark
    1. aggregateByKey的运行机制   /** * Aggregate the values of each key, using given combine functions and a neutral "zero value". * This function can return a different result type
  • hive创建表是报错： Specified key was too long; max key length is 767 bytes daizj hive
    今天在hive客户端创建表时报错，具体操作如下   hive> create table test2(id string); FAILED: Execution Error, return code 1 from org.apache.hadoop.hive.ql.exec.DDLTask. MetaException(message:javax.jdo.JDODataSto
  • Map 与 JavaBean之间的转换 周凡杨 java自省转换反射
    最近项目里需要一个工具类，它的功能是传入一个Map后可以返回一个JavaBean对象。很喜欢写这样的Java服务，首先我想到的是要通过Java 的反射去实现匿名类的方法调用，这样才可以把Map里的值set 到JavaBean里。其实这里用Java的自省会更方便，下面两个方法就是一个通过反射，一个通过自省来实现本功能。 1：JavaBean类 1 &nb
  • java连接ftp下载 g21121 java
    有的时候需要用到java连接ftp服务器下载，上传一些操作，下面写了一个小例子。 /** ftp服务器地址 */ private String ftpHost; /** ftp服务器用户名 */ private String ftpName; /** ftp服务器密码 */ private String ftpPass; /** ftp根目录 */ private String f
  • web报表工具FineReport使用中遇到的常见报错及解决办法（二） 老A不折腾 finereportweb报表java报表总结
      抛砖引玉，希望大家能把自己整理的问题及解决方法晾出来，Mark一下，利人利己。   出现问题先搜一下文档上有没有，再看看度娘有没有，再看看论坛有没有。有报错要看日志。下面简单罗列下常见的问题，大多文档上都有提到的。   1、没有返回数据集： 在存储过程中的操作语句之前加上set nocount on 或者在数据集exec调用存储过程的前面加上这句。当S
  • linux 系统cpu 内存等信息查看 墙头上一根草 cpu内存liunx
    1 查看CPU 　　1.1 查看CPU个数 　　# cat /proc/cpuinfo | grep "physical id" | uniq | wc -l 　　2 　　**uniq命令：删除重复行;wc –l命令：统计行数** 　　1.2 查看CPU核数 　　# cat /proc/cpuinfo | grep "cpu cores" | u
  • Spring中的AOP aijuans springAOP
      Spring中的AOP Written by Tony Jiang @ 2012-1-18 （转）何为AOP AOP，面向切面编程。 在不改动代码的前提下，灵活的在现有代码的执行顺序前后，添加进新规机能。 来一个简单的Sample: 目标类： [java]  view plain copy print ? package&nb
  • placeholder(HTML 5) IE 兼容插件 alxw4616 JavaScriptjquery jQuery插件
    placeholder 这个属性被越来越频繁的使用. 但为做HTML 5 特性IE没能实现这东西. 以下的jQuery插件就是用来在IE上实现该属性的. /** * [placeholder(HTML 5) IE 实现.IE9以下通过测试.] * v 1.0 by oTwo 2014年7月31日 11:45:29 */ $.fn.placeholder = function
  • Object类,值域,泛型等总结(适合有基础的人看) 百合不是茶 泛型的继承和通配符变量的值域Object类转换
    java的作用域在编程的时候经常会遇到,而我经常会搞不清楚这个 问题,所以在家的这几天回忆一下过去不知道的每个小知识点   变量的值域;   package 基础; /** * 作用域的范围 * * @author Administrator * */ public class zuoyongyu { public static vo
  • JDK1.5 Condition接口 bijian1013 javathreadConditionjava多线程
    Condition 将 Object 监视器方法（wait、notify和 notifyAll）分解成截然不同的对象，以便通过将这些对象与任意 Lock 实现组合使用，为每个对象提供多个等待 set （wait-set）。其中，Lock 替代了 synchronized 方法和语句的使用，Condition 替代了 Object 监视器方法的使用。 条件（也称为条件队列或条件变量）为线程提供了一
  • 开源中国OSC源创会记录 bijian1013 hadoopsparkMemSQL
    一.Strata+Hadoop World（SHW）大会         是全世界最大的大数据大会之一。SHW大会为各种技术提供了深度交流的机会，还会看到最领先的大数据技术、最广泛的应用场景、最有趣的用例教学以及最全面的大数据行业和趋势探讨。          二.Hadoop   &nbs
  • 【Java范型七】范型消除 bit1129 java
    范型是Java1.5引入的语言特性，它是编译时的一个语法现象，也就是说，对于一个类，不管是范型类还是非范型类，编译得到的字节码是一样的，差别仅在于通过范型这种语法来进行编译时的类型检查，在运行时是没有范型或者类型参数这个说法的。 范型跟反射刚好相反，反射是一种运行时行为，所以编译时不能访问的变量或者方法(比如private)，在运行时通过反射是可以访问的，也就是说，可见性也是一种编译时的行为，在
  • 【Spark九十四】spark-sql工具的使用 bit1129 spark
    spark-sql是Spark bin目录下的一个可执行脚本，它的目的是通过这个脚本执行Hive的命令，即原来通过 hive>输入的指令可以通过spark-sql>输入的指令来完成。 spark-sql可以使用内置的Hive metadata-store，也可以使用已经独立安装的Hive的metadata store   关于Hive build into Spark
  • js做的各种倒计时 ronin47 js 倒计时
    第一种：精确到秒的javascript倒计时代码      HTML代码:   <form name="form1">   <div align="center" align="middle"
  • java-37.有n 个长为m+1 的字符串，如果某个字符串的最后m 个字符与某个字符串的前m 个字符匹配，则两个字符串可以联接 bylijinnan java
    public class MaxCatenate { /* * Q.37 有n 个长为m+1 的字符串，如果某个字符串的最后m 个字符与某个字符串的前m 个字符匹配，则两个字符串可以联接， * 问这n 个字符串最多可以连成一个多长的字符串，如果出现循环，则返回错误。 */ public static void main(String[] args){
  • mongoDB安装 开窍的石头 mongodb安装 基本操作
    mongoDB的安装          1:mongoDB下载   https://www.mongodb.org/downloads         2:下载mongoDB下载后解压     
  • [开源项目]引擎的关键意义 comsci 开源项目
         一个系统，最核心的东西就是引擎。。。。。       而要设计和制造出引擎，最关键的是要坚持。。。。。。       现在最先进的引擎技术，也是从莱特兄弟那里出现的，但是中间一直没有断过研发的    
  • 软件度量的一些方法 cuiyadll 方法
    软件度量的一些方法http://cuiyingfeng.blog.51cto.com/43841/6775/在前面我们已介绍了组成软件度量的几个方面。在这里我们将先给出关于这几个方面的一个纲要介绍。在后面我们还会作进一步具体的阐述。当我们不从高层次的概念级来看软件度量及其目标的时候，我们很容易把这些活动看成是不同而且毫不相干的。我们现在希望表明他们是怎样恰如其分地嵌入我们的框架的。也就是我们度量的
  • XSD中的targetNameSpace解释 darrenzhu xmlnamespacexsdtargetnamespace
    参考链接: http://blog.csdn.net/colin1014/article/details/357694 xsd文件中定义了一个targetNameSpace后，其内部定义的元素，属性，类型等都属于该targetNameSpace,其自身或外部xsd文件使用这些元素，属性等都必须从定义的targetNameSpace中找： 例如：以下xsd文件，就出现了该错误，即便是在一
  • 什么是RAID0、RAID1、RAID0+1、RAID5，等磁盘阵列模式? dcj3sjt126com raid
    RAID 1又称为Mirror或Mirroring，它的宗旨是最大限度的保证用户数据的可用性和可修复性。 RAID 1的操作方式是把用户写入硬盘的数据百分之百地自动复制到另外一个硬盘上。由于对存储的数据进行百分之百的备份，在所有RAID级别中，RAID 1提供最高的数据安全保障。同样，由于数据的百分之百备份，备份数据占了总存储空间的一半，因而，Mirror的磁盘空间利用率低，存储成本高。 Mir
  • yii2 restful web服务快速入门 dcj3sjt126com PHPyii2
    快速入门 Yii 提供了一整套用来简化实现 RESTful 风格的 Web Service 服务的 API。 特别是，Yii 支持以下关于 RESTful 风格的 API： 支持 Active Record 类的通用API的快速原型 涉及的响应格式（在默认情况下支持 JSON 和 XML) 支持可选输出字段的定制对象序列化 适当的格式的数据采集和验证错误
  • MongoDB查询(3)——内嵌文档查询（七） eksliang MongoDB查询内嵌文档MongoDB查询内嵌数组
    MongoDB查询内嵌文档 转载请出自出处：http://eksliang.iteye.com/blog/2177301 一、概述        有两种方法可以查询内嵌文档：查询整个文档；针对键值对进行查询。这两种方式是不同的，下面我通过例子进行分别说明。   二、查询整个文档 例如:有如下文档 db.emp.insert({ &qu
  • android4.4从系统图库无法加载图片的问题 gundumw100 android
    典型的使用场景就是要设置一个头像，头像需要从系统图库或者拍照获得，在android4.4之前，我用的代码没问题，但是今天使用android4.4的时候突然发现不灵了。baidu了一圈，终于解决了。 下面是解决方案： private String[] items = new String[] { "图库","拍照" }; /* 头像名称 */
  • 网页特效大全 jQuery等 ini JavaScriptjquerycsshtml5ini
    HTML5和CSS3知识和特效 asp.net ajax jquery实例 分享一个下雪的特效 jQuery倾斜的动画导航菜单 选美大赛示例 你会选谁 jQuery实现HTML5时钟 功能强大的滚动播放插件JQ-Slide 万圣节快乐！！！ 向上弹出菜单jQuery插件 htm5视差动画 jquery将列表倒转顺序 推荐一个jQuery分页插件 jquery animate
  • swift objc_setAssociatedObject block(version1.2 xcode6.4) 啸笑天 version
      import UIKit class LSObjectWrapper: NSObject { let value: ((barButton: UIButton?) -> Void)? init(value: (barButton: UIButton?) -> Void) { self.value = value
  • Aegis 默认的 Xfire 绑定方式，将 XML 映射为 POJO MagicMa_007 javaPOJOxmlAegisxfire
          Aegis 是一个默认的 Xfire 绑定方式，它将 XML 映射为 POJO, 支持代码先行的开发.你开发服 务类与 POJO,它为你生成 XML schema/wsdl XML 和 注解映射概览       默认情况下，你的 POJO 类被是基于他们的名字与命名空间被序列化。如果
  • js get max value in (json) Array qiaolevip 每天进步一点点学习永无止境max纵观千象
    // Max value in Array var arr = [1,2,3,5,3,2];Math.max.apply(null, arr); // 5 // Max value in Jaon Array var arr = [{"x":"8/11/2009","y":0.026572007},{"x"
  • XMLhttpRequest 请求 XML,JSON ,POJO 数据 Luob. POJOjsonAjaxxmlXMLhttpREquest
    在使用XMlhttpRequest对象发送请求和响应之前，必须首先使用javaScript对象创建一个XMLHttpRquest对象。 var xmlhttp； function getXMLHttpRequest(){ if(window.ActiveXObject){ xmlhttp:new ActiveXObject("Microsoft.XMLHTTP
  • jquery wuai jquery
    以下防止文档在完全加载之前运行Jquery代码，否则会出现试图隐藏一个不存在的元素、获得未完全加载的图像的大小 等等 $(document).ready(function(){ jquery代码; }); <script type="text/javascript" src="c:/scripts/jquery-1.4.2.min.js&quo
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他