Annoy是高维空间求近似最近邻的一个开源库。
Annoy构建一棵二叉树,查询时间为O(logn)。
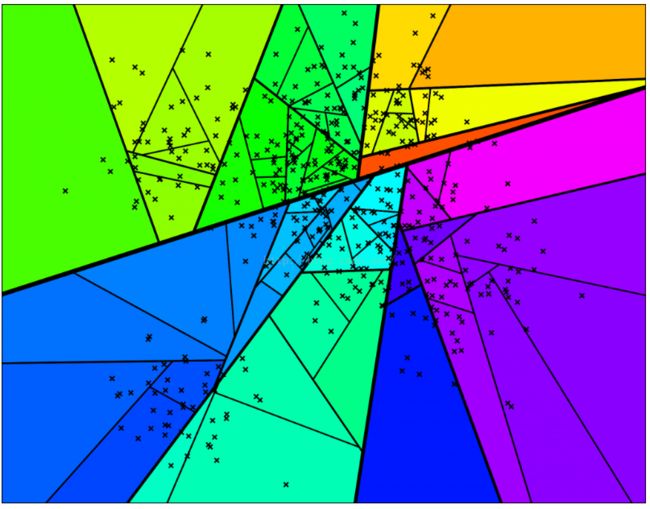
Annoy通过随机挑选两个点,并使用垂直于这个点的等距离超平面将集合划分为两部分。
如图所示,图中灰色线是连接两个点,超平面是加粗的黑线。按照这个方法在每个子集上迭代进行划分。
依此类推,直到每个集合最多剩余k个点,下图是一个k = 10 的情况。
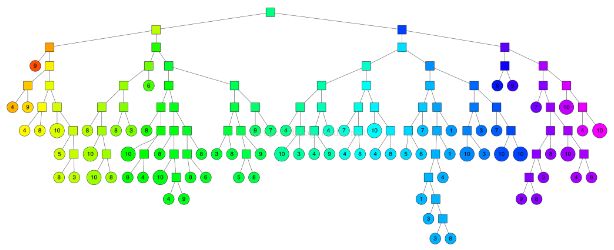
相应的完整二叉树结构:
随机投影森林。
一个思想依据是:在原空间中相邻的点,在树结构上也表现出相互靠近的特点,也就是说,如果两个点在空间上相互靠近,那么他们很可能被树结构划分到一起。
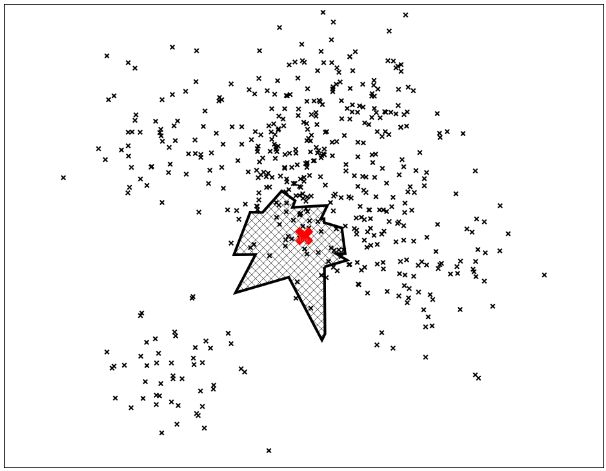
如果要在空间中查找临近点,我们可以在这个二叉树中搜索。上图中每个节点用超平面来定义,所以我们可以计算出该节点往哪个方向遍历,搜索时间 log n
如上图,我们找到了七个最近邻,但是假如我们想找到更多的最近邻怎么办?有些最近邻是在我们遍历的叶子节点的外边的。
技巧1:使用优先队列
如果一个划分的两边“靠得足够近”(量化方式在后面介绍),我们就两边都遍历。这样就不只是遍历一个节点的一边,我们将遍历更多的点
我们可以设置一个阈值,用来表示是否愿意搜索划分“错”的一遍。如果设置为0,我们将总是遍历“对”的一片。但是如果设置成0.5,就按照上面的搜索路径。
这个技巧实际上是利用优先级队列,依据两边的最大距离。好处是我们能够设置比0大的阈值,逐渐增加搜索范围。
技巧2:构建一个森林
我们能够用一个优先级队列,同时搜索所有的树。这样有另外一个好处,搜索会聚焦到那些与已知点靠得最近的那些树——能够把距离最远的空间划分出去
每棵树都包含所有的点,所以当我们搜索多棵树的时候,将找到多棵树上的多个点。如果我们把所有的搜索结果的叶子节点都合在一起,那么得到的最近邻就非常符合要求。
依照上述方法,我们找到一个近邻的集合,接下来就是计算所有的距离和对这些点进行排序,找到最近的k个点。
很明显,我们会丢掉一些最近的点,这也是为什么叫近似最近邻的原因。
Annoy在实际使用的时候,提供了一种机制可以调整(搜索k),你能够根据它来权衡性能(时间)和准确度(质量)。
tips:
1.距离计算,采用归一化的欧氏距离:vectors = sqrt(2-2*cos(u, v))
2.向量维度较小(<100),即使维度到达1000变现也不错
3.内存占用小
4.索引创建与查找分离(特别是一旦树已经创建,就不能添加更多项)
5.有两个参数可以用来调节Annoy 树的数量n_trees和搜索期间检查的节点数量search_k
n_trees在构建时提供,并影响构建时间和索引大小。 较大的值将给出更准确的结果,但更大的索引。
search_k在运行时提供,并影响搜索性能。 较大的值将给出更准确的结果,但将需要更长的时间返回。
如果不提供search_k,它将默认为n * n_trees,其中n是近似最近邻的数目。 否则,search_k和n_tree大致是独立的,即如果search_k保持不变,n_tree的值不会影响搜索时间,反之亦然。 基本上,建议在可用负载量的情况下尽可能大地设置n_trees,并且考虑到查询的时间限制,建议将search_k设置为尽可能大。
Python demo:
from annoy import AnnoyIndex import random f = 40 #维度 t = AnnoyIndex(f) # Length of item vector that will be indexed for i in xrange(1000): v = [random.gauss(0, 1) for z in xrange(f)] t.add_item(i, v) #添加向量 t.build(10) # 10 trees t.save('test.ann') # ... u = AnnoyIndex(f) u.load('test.ann') # super fast, will just mmap the file print(u.get_nns_by_item(0, 1000)) # will find the 1000 nearest neighbors of the first(0) vec
python API:
AnnoyIndex(f, metric='angular') returns a new index that's read-write and stores vector of f dimensions. Metric can be either "angular" or "euclidean".
a.add_item(i, v) adds item i (any nonnegative integer) with vector v. Note that it will allocate memory for max(i)+1 items.
a.build(n_trees) builds a forest of n_trees trees. More trees gives higher precision when querying. After calling build, no more items can be added.
a.save(fn) saves the index to disk.
a.load(fn) loads (mmaps) an index from disk.
a.unload() unloads.
a.get_nns_by_item(i, n, search_k=-1, include_distances=False) returns the n closest items. During the query it will inspect up to search_k nodes which defaults to n_trees * n if not provided. search_k gives you a run-time tradeoff between better accuracy and speed. If you set include_distances to True, it will return a 2 element tuple with two lists in it: the second one containing all corresponding distances.
a.get_nns_by_vector(v, n, search_k=-1, include_distances=False) same but query by vector v.
a.get_item_vector(i) returns the vector for item i that was previously added.
a.get_distance(i, j) returns the distance between items i and j. NOTE: this used to returned the squared distance, but has been changed as of Aug 2016.
a.get_n_items() returns the number of items in the index.
类似可以做这个工作的RPForest和sklearn.neighbors中的LSHForest,但Annoy的效果要比他们好很多。
查询树上所有节点都共用这个数据结构:
- n_descendants为该节点及其子孙节点包含的向量个数。
- children为左右子树指针。因为搜索树在物理上其实是这个结构体的数组,按照16字节对齐。搜索时把索引及数据文件mmap到内存,然后通过数组下标进行随机定位。所以指针就是数组下标