栈和队列:面试题(Java)
文章目录
- 两个队列实现一个栈
- 两个栈实现一个队列
- 中缀表达式转后缀表达式
- 计算后缀表达式(逆波兰表达式)
- 深度优先遍历迷宫
- 广度优先遍历迷宫:找最短路径
两个队列实现一个栈
使用两个队列完成栈的功能,
思路:
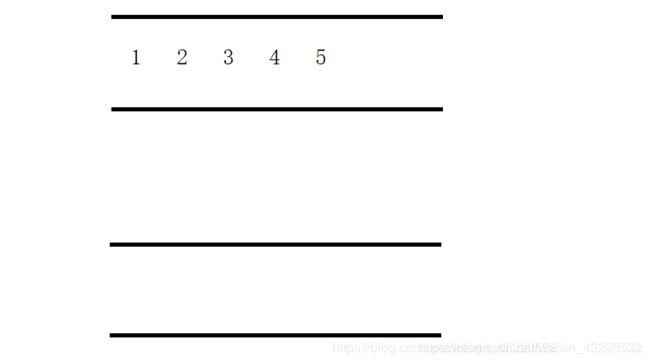
如上图,入队顺序为:1 2 3 4 5,如果要模拟栈的功能,那么就要上5先弹出来,因为是队列,所以只能从1开始出,把1 2 3 4存到另外一个队列中,这样就可以把5弹出来了:
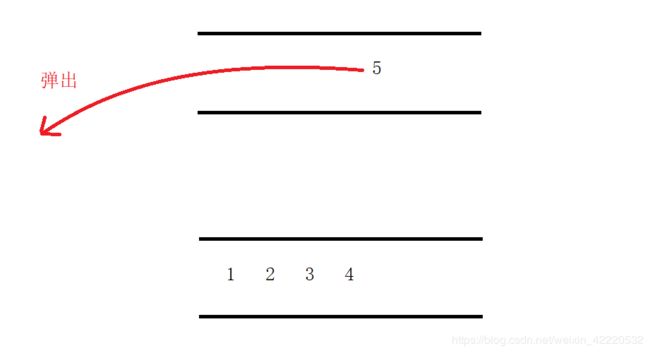
这样就完成了一次出栈,这下上面的队列为空,所有的数据存储在下面这个队列中:
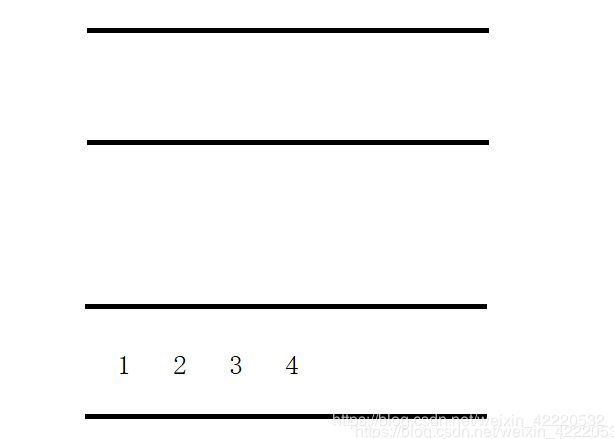
如果要继续出栈,那么就把1 2 3 挪到空的队列中,弹出4,到这里已经明白了如何模拟出栈,如何入栈呢,如果现在要入栈6,就直接跟到1 2 3 4的后面即可
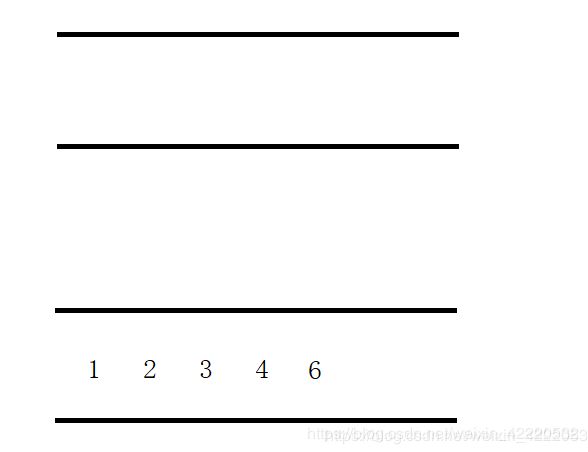
这样出栈还是符合上面的规则,所以总结为两句话:
- 入栈时把数据入到有数据的那个队列中
- 出栈时把有数据的队列中的数据除过最后一个,其他都入队到另外一个队列,最后一个就是要出栈的元素
代码实现:
/**
* 实现两个队列实现一个栈
*/
public class StackQueue1 {
private LinkedList<Integer> list1;
private LinkedList<Integer> list2;
public StackQueue1() {
list1 = new LinkedList<>();
list2 = new LinkedList<>();
}
/**
* 入栈
*/
public void push(int data) {
if(!list1.isEmpty()) {
list1.offer(data);
} else {
//默认栈为空的时候都入栈到list2
list2.offer(data);
}
}
/**
* 出栈
*/
public Integer pop() {
if(isEmpty()) {
return null;
}
//srcList表示有数据的队列,destList表示没有数据的队列
LinkedList<Integer> srcList = list1;
LinkedList<Integer> destList = list2;
if(list1.isEmpty()) {
srcList = list2;
destList = list1;
}
Integer poll = null;
while(!srcList.isEmpty()) {
poll = srcList.poll();
//如果是最后一次出队,那么不再把最后一个元素入队到另一个队列中
if(srcList.isEmpty()) {
break;
}
destList.offer(poll);
}
return poll;
}
/**
* 判断栈空
* @return
*/
private boolean isEmpty() {
return list1.isEmpty() && list2.isEmpty();
}
}
两个栈实现一个队列
思路:
把1 2 3 4 5入栈到左边的栈中
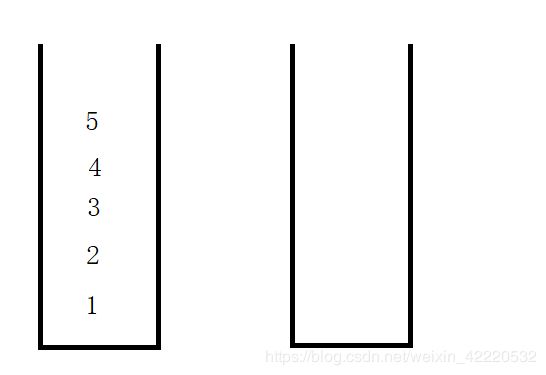
然后把所有的元素从左边倒到右边
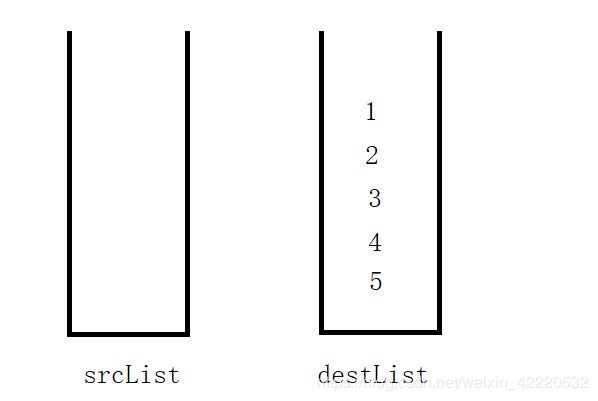
如果要出队,这下右边的destList的出栈就完全等同于出队,所以把右边的固定位出队的,把srcList固定为入队的,如果右边的destList为空,那么就再一次把左边的srcList倒到右边的destList中,循环往复。
代码:
/**
* 两个栈实现一个队列
*/
public class StackQueue2 {
private LinkedList<Integer> srcList;
private LinkedList<Integer> destList;
public StackQueue2() {
srcList = new LinkedList<>();
destList = new LinkedList<>();
}
/**
* 入队
*/
public void offer(int data) {
srcList.push(data);
}
/**
* 出队
*/
public Integer poll() {
if(isEmpty()) {
return null;
}
if(destList.isEmpty()) {
//把srcList中的数据都搬过来
while(!srcList.isEmpty()) {
Integer pop = srcList.pop();
destList.push(pop);
}
}
return destList.pop();
}
/**
* 判断队列是否为空
* @return
*/
private boolean isEmpty() {
return srcList.isEmpty() && destList.isEmpty();
}
}
中缀表达式转后缀表达式
计算机是通过后缀表达式来认识四则运算,而对于中缀表达式比如:
4+2*3
计算机是不知道优先级的,如果把该式转为后缀表达式
4 2 3 * +
对于后缀表达式,计算机通过一个栈便能轻松的按照优先级来计算结果,上式计算即会先把 4 2 3 进行入栈,遇到 * 操作符后,把2 3 出栈进行计算,计算的结果再次入栈,如果下次再碰到运算符,继续从栈中取出两个数进行运算。
先来进行第一步,如何把中缀表达式转为后缀表达式?
其实该过程也是借助一个栈来完成的,该栈用来存储操作符,而遇到数字就直接输出,遇到操作符则通过栈来调整操作符的顺序,入栈出栈的规则有以下几条:
1.如果栈(指操作符栈,下面用栈代替)为空,那么遇到操作符直接入栈
2.如果遇到 ( ,则直接入栈,( 的优先级是最小的,( 的存在就是为了等待 ) 来进行配对
3.如果遇到 ) ,那么一直出栈,直到遇到 (
4.如果该操作符比栈顶的操作符的优先级大,那么把该操作符入栈
5.如果该操作符的优先级小于等于栈顶操作符,那么一直出栈到该操作符大于栈顶为止,最后把该操作符入栈
由于在运算中会存在多位的数字,如
10*2+2
10就是一个多位数字,所以我们肯定不能用字符去处理,代码中我用到了StringBuilder
有了这几条规则,直接来看一下代码实现:
public class StackQueue3 {
public static void main(String[] args) {
System.out.println(fun1("4+2*3"));
}
public static LinkedList<String> fun1(String expression) {
//操作符栈
LinkedList<Character> stack = new LinkedList<>();
//用来存储后缀表达式
LinkedList<String> backExpression = new LinkedList<>();
//用来构造多位数字
StringBuilder stringBuilder = new StringBuilder();
for (int i = 0; i < expression.length(); i++) {
char c = expression.charAt(i);
//先判断是否是数字
if(Character.isDigit(c)) {
stringBuilder.append(c);
} else {
//遇到了操作数,先把多位数从StringBuilder中拿出来
if(stringBuilder.length() != 0) {
backExpression.addLast(stringBuilder.toString());
//添加完后把StringBuilder清空
stringBuilder.delete(0,stringBuilder.length());
}
//1.如果栈为空
if(stack.isEmpty()) {
stack.push(c);
} else if(c==')') {
//3.如果等于 ) ,一直出栈直到遇到 (,把中间的操作符直接添加到后缀表达式链表中
while(true) {
Character pop = stack.pop();
if(pop == '(') {
break;
}
backExpression.addLast(String.valueOf(pop));
}
} else if(c=='(') {
//2.如果等于 (
stack.push('(');
} else if(isBig(c,stack.peek())) {
//4.如果该操作符优先级大于栈顶
stack.push(c);
} else {
//5.如果该操作符优先级小于等于
while (true) {
Character pop = stack.pop();
backExpression.addLast(String.valueOf(pop));
if(isBig(c,stack.peek())) {
stack.push(c);
break;
}
}
}
}
}
//缓冲中可能还有数字
backExpression.addLast(stringBuilder.toString());
stringBuilder.delete(0,stringBuilder.length());
//最后把所有的操作符出栈
while(!stack.isEmpty()) {
backExpression.addLast(String.valueOf(stack.pop()));
}
return backExpression;
}
/**
* 判断优先级大小
* @param c
* @param peek
* @return
*/
private static boolean isBig(char c, Character peek) {
if(peek == null) {
//null,即栈为空,那么返回true让操作符直接入栈
return true;
}
/**
* 优先级大于,为true有两种情况
* 1.操作符为:*,/ 栈顶:+ ,-
* 2.栈顶为 ( ,那么括号的优先级肯定大,要把所有在括号内的操作符都入栈
*/
return ((c=='*'||c=='/')&&(peek=='+'||peek=='-')) || peek=='(' ;
}
}
计算后缀表达式(逆波兰表达式)
计算机进行四则运算的第二步,就是计算后缀表达式,上面也已经讲过了,计算逆波兰表达式比较简单,只需要一个操作数栈,遇到数字就入栈,遇到操作符时就从操作数栈取出左右两个数字进行计算,然后把计算的结果入栈,到最后栈中只剩下一个数字,那么就是最后的结果。
代码实现:
public static Integer fun2(LinkedList<String> backExpression) {
//创建操作数栈
LinkedList<Integer> stack = new LinkedList<>();
Iterator<String> iterator = backExpression.iterator();
while(iterator.hasNext()) {
String next = iterator.next();
//判断是否操作符
if(next.equals("+") || next.equals("-") || next.equals("*") || next.equals("/")) {
Integer right = stack.pop();
Integer left = stack.pop();
Integer result = null;
if(next.equals("+")) {
result = left + right;
} else if(next.equals("-")) {
result = left - right;
} else if(next.equals("*")) {
result = left * right;
} else {
result = left / right;
}
stack.push(result);
} else {
stack.push(Integer.parseInt(next));
}
}
return stack.peek();
}
深度优先遍历迷宫
输入一个二维数组,1表示不可走,0表示可走,然后利用栈来找到迷宫的通路,通路是从左上角往右下角找,右下角是出口。
利用栈来进行深度优先遍历,深度优先意思就是先往深进行遍历,当深度不能再往下,那么就进行回退,回退后再次进行深度。
class MazeNode {
//x坐标
private int x;
//y坐标
private int y;
//记录左边是否可走
private boolean left;
//记录右边是否可走
private boolean right;
//记录上边是否可走
private boolean up;
//记录下边是否可走
private boolean down;
//0表示可走,1表示不可走,6表示正确路线
private int value;
public MazeNode(int x,int y) {
this.x = x;
this.y = y;
this.left = true;
this.right = true;
this.up = true;
this.down = true;
}
public MazeNode() {
this(-1,-1);
}
public int getValue() {
return value;
}
public void setValue(int value) {
this.value = value;
}
public int getX() {
return x;
}
public void setX(int x) {
this.x = x;
}
public int getY() {
return y;
}
public void setY(int y) {
this.y = y;
}
public boolean isLeft() {
return left;
}
public void setLeft(boolean left) {
this.left = left;
}
public boolean isRight() {
return right;
}
public void setRight(boolean right) {
this.right = right;
}
public boolean isUp() {
return up;
}
public void setUp(boolean up) {
this.up = up;
}
public boolean isDown() {
return down;
}
public void setDown(boolean down) {
this.down = down;
}
@Override
public String toString() {
return "MazeNode{" +
"value=" + value +
'}';
}
}
Maze类:
public class Maze {
private static MazeNode[][] maze;
public static void main(String[] args) {
//完成整个迷宫二维数组的建立
Scanner scanner = new Scanner(System.in);
System.out.println("请输入迷宫共有多少行");
int row = scanner.nextInt();
System.out.println("请输入迷宫共有多少列");
int col = scanner.nextInt();
maze = new MazeNode[row][col];
System.out.println("输入迷宫的元素");
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
int next = scanner.nextInt();
maze[i][j] = new MazeNode(i,j);
maze[i][j].setValue(next);
}
}
maze();
}
private static void maze() {
//创建一个栈,用来深度优先遍历
LinkedList<MazeNode> stack = new LinkedList<>();
//确定入口
stack.push(maze[0][0]);
//要么栈空退出,要么到出口退出
while (stack.peek() != null && (stack.peek().getX()!=maze.length-1 || stack.peek().getY()!=maze[0].length-1)) {
//拿到栈顶
MazeNode peek = stack.peek();
int x = peek.getX();
int y = peek.getY();
//判断向下是否可走
if((x+1)<maze.length && maze[x+1][y].getValue()==0 && maze[x][y].isDown()) {
//先把来回的路封死
maze[x][y].setDown(false);
maze[x+1][y].setUp(false);
//下面可走,则直接把下一个元素入栈,从下一个节点开始走
stack.push(maze[x+1][y]);
continue;
} else if((y+1)<maze[0].length && maze[x][y+1].getValue() == 0 && maze[x][y].isRight()) {
//往右走
maze[x][y].setRight(false);
maze[x][y+1].setLeft(false);
//成功走到右边,入栈
stack.push(maze[x][y+1]);
continue;
} else if((y-1)>=0 && maze[x][y-1].getValue()==0 && maze[x][y].isLeft()) {
//往左走
maze[x][y].setLeft(false);
maze[x][y-1].setRight(false);
stack.push(maze[x][y-1]);
continue;
} else if((x-1)>=0 && maze[x-1][y].getValue()==0 && maze[x][y].isUp()) {
//往上走
maze[x][y].setUp(false);
maze[x-1][y].setDown(false);
stack.push(maze[x-1][y]);
continue;
}
stack.pop();
}
if(stack.peek() == null) {
System.out.println("没有找到路径");
} else {
while(!stack.isEmpty()){
MazeNode pop = stack.pop();
pop.setValue(6);
}
//打印路径
for (int i = 0; i < maze.length; i++) {
for (int j = 0; j < maze[0].length; j++) {
System.out.print(maze[i][j].getValue()+" ");
}
System.out.println();
}
}
}
}
广度优先遍历迷宫:找最短路径
通过深度遍历只能找出迷宫的一条路径,但是确不能得到迷宫的最短路径,因为深度的思路是只要有路走,就一直走,走到死胡同再往上退,退到有路的地方继续往下走,有一点暴力的意思。
举个例子,来看一组测试:

在上面的代码中我先规定走的顺序是:下右左上,而我调整为:右下左上
通过调整后测试明显可以看到,走了弯路,所以就需要广度优先遍历来解决这个问题
广度优先遍历的思路是:借助一个队列,把队头节点的上下左右可以走的节点都入队,检索完后将队头出队,继续采集队头,然后检查上下左右,最终如果入队的是右下角的出口,则已经找到了通路,结束整个寻找过程。
这个其实就是在广度上进行拓展,每一个节点都去找所有可以走的路,利用队列先入先出的特点,存储了可以走的所有通路,然后每条通路一次都走一步,当然走一步又有新的通路加进来,最终先入队出口节点的就是最短的。
找到出口后,队列中并不是真正的路径,而是鱼龙混杂的几条没有走完的路径,这就需要我们使用一个数组来记录每一步走的过程,也就是该节点是由于哪个节点入队的,中间是如何跳跃的。
在代码是我们可以套用刚才写好的深度,把栈换成队列,并且加入一个二维数组来记录整个路径,在最后写入正确路径的时候需要进行修改,一起来看一下:
public class Maze2 {
private static MazeNode[][] maze;
public static void main(String[] args) {
//完成整个迷宫二维数组的建立
Scanner scanner = new Scanner(System.in);
System.out.println("请输入迷宫共有多少行");
int row = scanner.nextInt();
System.out.println("请输入迷宫共有多少列");
int col = scanner.nextInt();
maze = new MazeNode[row][col];
System.out.println("输入迷宫的元素");
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
int next = scanner.nextInt();
maze[i][j] = new MazeNode(i,j);
maze[i][j].setValue(next);
}
}
maze();
}
private static void maze() {
//创建一个队列来进行广度优先搜索
LinkedList<MazeNode> queue = new LinkedList<>();
//定义一个数组记录跳跃的过程
MazeNode[][] mazeRecord = new MazeNode[maze.length][maze[0].length];
//确定入口
queue.push(maze[0][0]);
while (queue.peek() != null) {
//拿到队头
MazeNode peek = queue.peek();
int x = peek.getX();
int y = peek.getY();
if((y+1)<maze[0].length && maze[x][y+1].getValue() == 0 && maze[x][y].isRight()) {
//往右走
maze[x][y].setRight(false);
maze[x][y+1].setLeft(false);
//成功走到右边,入队
queue.offer(maze[x][y+1]);
//记录轨迹
mazeRecord[x][y+1] = maze[x][y];
//如果入队的是出口,说明已经找到,直接返回
if(check(x,y+1)) {
break;
}
}
if((x+1)<maze.length && maze[x+1][y].getValue()==0 && maze[x][y].isDown()) {
//判断向下是否可走
//先把来回的路封死
maze[x][y].setDown(false);
maze[x+1][y].setUp(false);
//下面可走,则直接把下一个元素入栈,从下一个节点开始走
queue.offer(maze[x+1][y]);
//记录轨迹
mazeRecord[x+1][y] = maze[x][y];
//如果入队的是出口,说明已经找到,直接返回
if(check(x+1,y)) {
break;
}
}
if((y-1)>=0 && maze[x][y-1].getValue()==0 && maze[x][y].isLeft()) {
//往左走
maze[x][y].setLeft(false);
maze[x][y-1].setRight(false);
queue.offer(maze[x][y-1]);
//记录轨迹
mazeRecord[x][y-1] = maze[x][y];
//如果入队的是出口,说明已经找到,直接返回
if(check(x,y-1)) {
break;
}
}
if((x-1)>=0 && maze[x-1][y].getValue()==0 && maze[x][y].isUp()) {
//往上走
maze[x][y].setUp(false);
maze[x-1][y].setDown(false);
queue.offer(maze[x-1][y]);
//记录轨迹
mazeRecord[x-1][y] = maze[x][y];
//如果入队的是出口,说明已经找到,直接返回
if(check(x-1,y)) {
break;
}
}
queue.poll();
}
if(queue.peek() == null) {
System.out.println("没有找到路径");
} else {
int x = maze.length-1;
int y = maze[0].length-1;
//修改正确路径
while(true) {
maze[x][y].setValue(6);
if(x==0 && y==0) {
break;
}
MazeNode temp = mazeRecord[x][y];
x = temp.getX();
y = temp.getY();
}
//打印路径
for (int i = 0; i < maze.length; i++) {
for (int j = 0; j < maze[0].length; j++) {
System.out.print(maze[i][j].getValue()+" ");
}
System.out.println();
}
}
}
//检查入队的是否是出口
private static boolean check(int x, int y) {
return x==maze.length-1 && y==maze[0].length-1;
}
}



