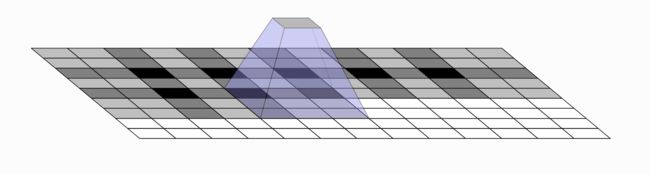
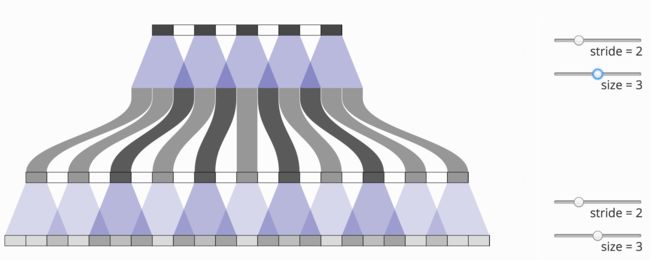
当我们非常仔细地观察神经网络生成的图像时,经常会看到一些奇怪的棋盘格子状的伪影(artifact)。这种现象在有些情况下比在其他情况下更明显,但最近的模型很多都会出现这种现象。
不可思议的是,这些棋盘图案在颜色深的图像中最突出。这是怎么回事?神经网络讨厌明亮的颜色吗?这些伪影出现的实际原因其实非常简单,解决方法也非常简单。
反卷积&重叠
当我们用神经网络生成图像时,我们经常从低分辨率与高阶描述构建图像。这会让网络先描绘粗糙的图像,再填充细节。
为此,我们需要能让图像从较低的分辨率转为较高分辨率的方法。我们通常使用反卷积操作。大致来说,反卷积层允许模型使用小图像中的每个点来“绘制”更大图像中的方块。
(反卷积有许多不同的理解方式与不同的名字,包括“转置卷积”。为了简洁起见,本文使用“反卷积”。有关反卷积的更多讨论参见:Dumoulin & Visin, 2016 and Shi, et al., 2016a.)
不幸的是,反卷积很容易“不均匀重叠”,使图像中的某个部位的颜色比其他部位更深(Gauthier, 2015)。尤其是当核大小(输出窗口的大小)不能被步长(顶层点之间的空间)整除时,反卷积就会不均匀重叠。虽然原则上网络可以仔细地学习权重来避免这种情况,就像我们接下来会仔细探讨的那样,但在实践中神经网络很难完全避免不均匀重叠。
重叠图案也在二维中形成。两个轴上的不均匀重叠相乘,产生不同亮度的棋盘状图案。
事实上,不均匀重叠往往在二维上更极端!因为两个模式相乘,它的不均匀性是原来的平方。例如,在一个维度中,一个步长为2,大小为3的反卷积的输出是其输入的两倍,但在二维中,输出是输入的四倍。
现在,生成图像时,神经网络通常使用多层反卷积,从一系列较低分辨率的描述中迭代建立更大的图像。虽然这些堆栈的反卷积可以消除棋盘效应,但它们经常混合,在更多尺度上产生棋盘效应。
步长为1的反卷积层——通常被认为是成功的模型中的最后一层(eg. Salimans et al., 2016)——在减轻棋盘效应方面非常有效。它们可以消除频率整除其大小的棋盘效应,也可以减少其他频率小于其大小的棋盘效应。但是,棋盘效应仍然会发生,就像最近的模型出现的。
除了我们在上文观察到的高频棋盘状伪影外,早期的反卷积可以产生较低频率的伪影,我们将在后文更详细地探讨。
重叠&学习
不均匀重叠虽然是有效的框架,也可以说它是一种简单化。无论好坏,模型要为它们的反卷积学习权重。
理论上,模型可以学习仔细地写入不均匀重叠的位置,以使输出均匀平衡。
这种平衡行为的实现相当棘手,尤其是当模型有多个交互通道时。避免棋盘效应会显著限制可能的过滤器,牺牲模型容量。在实践中,神经网络很难学习完全避免这些模式。
事实上,不仅具有不均匀重叠的模型不会学习避免这种情况,而且均匀重叠的模型也经常学习会导致类似的棋盘效应的核!虽然对它们来说这不是默认的行为,不像不均匀重叠模型。但均匀重叠反卷积仍然非常容易产生棋盘效应。
最好的情况下,反卷积非常脆弱,因为它非常容易呈现人工创造的功能。最坏的是,产生棋盘效应是反卷积的默认行为。
那么,是否有一种不同的上采样(upsample)方法能更好地阻止棋盘效应?
方法之一是确保反卷积核的大小可以被步长整除,从而避免重叠问题。这等价于最近成功用于图像超分辨率解析的技术“子像素卷积”(sub-pixel convolution) (Shi, et al., 2016b)。但是,尽管这种方法有效,但反卷积仍然容易产生棋盘效应。
另一种方法是将上采样分离为较高分辨率的卷积到计算特征。例如,您可以调整图像大小(使用最近邻居插值或双线性插值),然后进行卷积层。这似乎是一个自然的方法,大致类似的方法在图像超分辨率(例如,Dong,et al。,2015)中工作良好。
另一种方法是从卷积操作中分离出对卷积后更高分辨率的特征图上采样来计算特征。例如,可以先缩放图像(最近邻插值或双线性插值),再卷积。这似乎是自然的方法。
更好的上采样方法
为了避免棋盘效应,我们想要一个常规反卷积的代替方法。与反卷积不同,这种上采样方法默认不应发生棋盘效应。理想情况下,它会进一步对抗这些棋盘效应。
反卷积与缩放卷积(resize-convolution)方法都是线性操作,并可用矩阵去解释。对于每个输出窗口,反卷积操作的输入唯一,缩放卷积会以阻碍高频棋盘效应的方式来隐式地集中权重(weight-tying)。
代码:
在TensorFlow实现缩放卷积可以使用以下代码:tf.image.resize_images()
为了得到最好的结果,在用tf.nn.conv2d()做卷积前可以用tf.pad()避免边界效应。
图像生成结果
我们得到的结果让卷积层前的最邻近点的尺寸大小调整可以很好的工作,并且适用于多种情况。我们发现这一方法有用的一个例子是对抗生成网络。(在对抗生成网络中)只需简单地断开标准去卷积层(这些去卷积层用于最邻近点的尺寸调整,紧随其后的是卷积层),就能让不同的序列中的 Artifacts 消失。
事实上,在展开任何训练之前,Artifacts是可见的。如果我们看生成器产出的图像,也就是使用随机权重得出的最初结果,我们已经能看到 artifacts:这表明了,Artifacts 取决于生成图像的方法,而不是对抗训练。(还表明我们也许能够在不需要那些反馈周期很长的训练模型的情况下,学习到好的生成器设计。)
这些 Artifacts 并不是 GAN(对抗生成网络)的另一个原因是,在别的类型的模型中也见到过它们,并发现在转换到 尺寸调整卷积(resize-convolution)上采样时,它们也会消失。例如,在实时的艺术风格转换中,神经网络被训练后直接生成变化风格的图像。我们发现,在这种情况下,这些转换很容易产生棋盘效应(checkerboard artifacts),尤其是在没有专门准备应对方案的时候。
但是,在尺寸调整卷积层中调整去卷积层能让这些“棋盘效应”消失。谷歌大脑团队在接下来的论文中将会用更加连贯的实验和更先进的结果,展示这种技术的优势。(我们选择提前单独公开这一技术,是因为它值得有更多细节的讨论,也因为它包含了多篇论文的结果。)
梯度中的 Artifacts
不管什么时候,只要计算一个卷积层的梯度,我们就要在反馈通道中进行一次去卷积(转置卷积,transposed convolution)。这一过程导致了在梯度中会产生棋盘模式,正如我们使用去卷积生成图像遇到的问题一样。
在特征可视化领域,图像模型梯度中“噪音”的频繁出现是一个巨大的挑战。从某种程度上来说,特征可视化的方法必须要对这些噪音做出补偿。
例如,DeepDream 似乎会在不同的 Artifacts 间引发破坏性的干扰,比如,在同时对多个特征 ,或者在多个偏移(offsets)与尺度(scales)中进行优化的时候。尤其值得一提的是,不同偏移中优化时产生的“抖动”(jitter),抵消了一些棋盘效应。 (虽然大多数的Artifacts是我们标准的棋盘模型,但是其他则是无组织的高频率模型。我相信这是由于最大池化造成的。Henaff 和 Simoncelli 在2015年的论文中曾提出,高频率的Artifacts与最大池化有关。)
在特征可视化上,更多最新的研究明确地识别和补偿这些高频率的梯度组建。一个问题是,有没有更好的神经网络架构,可以让这些工作变成“非必要”选项。
这些梯度Artifacts 影响了GAN?如果梯度 Artifacts 能影响一个被优化的图像,在特征可视化中,这些图像基于一个神经网络梯度,我们还期待,也许它也会影响由生成器参数化的图像集,因为它们都是在GAN中通过鉴别器进行优化。
我们发现,在一些情况下,上述情况确实会发生。当生成器既不偏向或反对棋盘模型,辨别器中的大步卷积就会引发上述情况。现在还不清楚这些梯度Artifacts会不会带来更加宽泛的影响。一个思路是,一些神经元将会回相邻的神经元中多次获得梯度,而且是任意的。同等的,网络也会偏重于输入中的一些像素,具体原因还不清楚。
似乎,一些像素会比其他像素更严重地影响输出这一事实,会夸大了对抗性反样本的作用。因为派生只聚焦于小量的像素,这些像素中一小部分的干扰可能会有大的影响。我们还没有研究这一点。
结论
用反卷积的常规方法生成图像(尽管这种方法非常成功),在概念上仍然存在一些非常简单的问题,使得在生成的图像中出现棋盘效应。使用一种自然的替代方法,避免掉这些问题,可以消除棋盘效应。(一些研究表明,标准的大步卷积层可能也有问题)。
这对我们来说是一个激动人心的机会。它表明,可以在神经网络架构中通过谨慎地思考,寻找一种低门槛的方法,这种方法能让我们找到清晰的解决问题的方法。
我们提供了一个易用的解决方案,提高了用神经网络生成图像的质量。我们期待看到这种方法会被怎样使用,以及它是否能对音频之类的领域有所帮助,这类领域中的高频伪影是尤其棘手的问题。
http://distill.pub/2016/deconv-checkerboard/