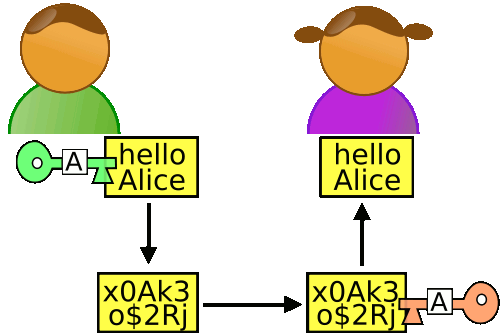
关于实现RSA的具体算法
1.素性判断
Prime.py
# coding:utf-8
import math
import random
# 扩展欧几里得算法求模反元素
def ex_euclid(a, b, list):
if b == 0:
list[0] = 1L
list[1] = 0L
list[2] = a
else:
ex_euclid(b, a % b, list)
temp = list[0]
list[0] = list[1]
list[1] = temp - a / b * list[1]
# 求模反元素
def mod_inverse(a, b):
list = [0L, 0L, 0L]
if a < b:
a, b = b, a
ex_euclid(a, b, list)
if list[1] < 0:
list[1] = a + list[1]
return list[1]
# 快速幂模运算,把b拆分为二进制,遍历b的二进制,当二进制位为0时不计入计算
def quick_pow_mod(a, b, c):
a = a % c
ans = 1
while b != 0:
if b & 1:
ans = (ans * a) % c
b >>= 1
a = (a % c) * (a % c)
return ans
# n为要检验的大数,a < n,k = n - 1
def miller_rabin_witness(a, n):
if n == 1:
return False
if n == 2:
return True
k = n - 1
q = int(math.floor(math.log(k, 2)))
while q > 0:
m = k / 2 ** q
if k % 2 ** q == 0 and m % 2 == 1:
break
q = q - 1
if quick_pow_mod(a, n - 1, n) != 1:
return False
b1 = quick_pow_mod(a, m, n)
for i in range(1, q + 1):
if b1 == n - 1 or b1 == 1:
return True
b2 = b1 ** 2 % n
b1 = b2
if b1 == 1:
return True
return False
# Miller-Rabin素性检验算法,检验8次
def prime_test_miller_rabin(p, k):
while k > 0:
a = random.randint(1, p - 1)
if not miller_rabin_witness(a, p):
return False
k = k - 1
return True
# 判断 num 是否与 prime_arr 中的每一个数都互质
def prime_each(num, prime_arr):
for prime in prime_arr:
remainder = num % prime
if remainder == 0:
return False
return True
# return a prime array from begin to end
def get_con_prime_array(begin, end):
array = []
for i in range(begin, end):
flag = judge_prime(i)
if flag:
array.append(i)
return array
# judge whether a number is prime
def judge_prime(number):
temp = int(math.sqrt(number))
for i in range(2, temp + 1):
if number % i == 0:
return False
return True
# 根据 count 的值生成若干个与质数数组都互质的大数
def get_rand_prime_arr(count):
arr = get_con_prime_array(2, 100000)
prime = []
while len(prime) < count:
num = random.randint(pow(10, 100), pow(10, 101))
if num % 2 == 0:
num = num + 1
while True:
if prime_each(num, arr) and prime_test_miller_rabin(num, 8):
if num not in prime:
prime.append(num)
break
num = num + 2
return prime
2.RSA具体实现
RSA.py
# coding:utf-8
import random
import Prime
# encryption ,according to the formula:m^e = c (mod n) , calculate c ,c == secret,m == message
def encryption(message, puk):
return Prime.quick_pow_mod(message, puk[1], puk[0])
# decryption ,according to the formula:c^d = m (mod n), calculate m ,
def decryption(secret, prk):
return Prime.quick_pow_mod(secret, prk[1], prk[0])
def get_RSAKey():
RSAKey = {}
prime_arr = Prime.get_rand_prime_arr(2)
p = prime_arr[0]
q = prime_arr[1]
while p == q:
q = random.choice(prime_arr)
n = p * q
s = (p - 1) * (q - 1)
e = 65537
d = Prime.mod_inverse(e, s)
print "p = ", p, ",q = ", q
print "n = ", n
print "e = ", e, ",d = ", d
puk = [n, e]
prk = [n, d]
RSAKey['puk'] = puk
RSAKey['prk'] = prk
return RSAKey
if __name__ == '__main__':
RSAKey = get_RSAKey()
print "Enter a number less and shorter than ", len(str(RSAKey['puk'][0])), ",", RSAKey['puk'][0], ":"
# only encrypt a number type
message = int(input())
secret = encryption(message, RSAKey['puk'])
print "After the encryption data :", secret
print len(str(secret))
message = decryption(secret, RSAKey['prk'])
print "After the decryption data :", message
print len(str(message))