stata连享会
stata连享会

连享会-倍分法DID详解 (一)：传统 DID

 

作者：王昆仑 (天津大学)

Stata 连享会： 知乎 | | 码云 | CSDN

 

  • Stata连享会 计量专题 || 公众号合集
    连享会-倍分法DID详解 (一)：传统 DID_第1张图片
    点击查看完整推文列表

连享会：内生性问题及估计方法专题

连享会-倍分法DID详解 (一)：传统 DID_第2张图片
连享会-内生性专题现场班-2019.11.14-17

连享会#金秋十月 @ 空间计量专题 (2019.10.24-27,成都)

连享会-倍分法DID详解 (一)：传统 DID_第3张图片
2019.10-杨海生-空间计量专题-连享会

导入

双重差分模型 （Difference-Differences, DID）是政策评估的非实验方法中最为常用的一种方法。本系列推文的目的是，利用模拟的方式直观的展示 Standard DID，Time-varying DID 以及其于Event Study Approach (ESA) 的结合应用。

一、引言

关于 DID 方法的推文已经不少了，仅连享会就推送过 Stata: 双重差分的固定效益模型 和 多期DID：平行趋势检验图示 两篇专题文章，还有利用 margins 命令来计算 DID 模型的边际效果的推文 DID 边际分析：让政策评价结果更加丰满 。另外，李春涛老师的爬虫俱乐部公众号也用两期的篇幅来对DID模型和其平行趋势的检验做了简要的介绍。对于 DID 方法可能还不是熟悉的同学，可以结合陈强老师的推文和参考资料里提到的内容一起学习。

与上述的文章相比，这一系列推文有以下三点优势：第一，本系列将上述的 DID 模型的设置，平行趋势的检验和图形表示以及边际效果等一般化的流程尽可能地在一篇推文中展示出来，为读者作为参考；第二，本系列利用同一套的模拟数据，将 Standard DID 以及 Time-varying DID 结合起来，
分析其方程设定的异同；第三，在实际的操作过程中，Time-varying DID 利用 ESA 方法对平行趋势进行检验时，由于可能存在不是所有
个体都最终接受了政策干预，因此，这两种情况下，ESA 方程的设定和代码写作存在差异，这也是本系列推文所着重关心的问题。

二、模拟数据的生成

我重新生成了一份模拟数据，结构为 60 个体*10年共600个观测值的平衡面板数据。我们在数据中设定 2005 年为政策发生当年，id 30-60的个体为处理组，剩余的个体形成控制组。我们将基础的文件保存为DID_Basic_Simu.dta文件，方便后面调用。

///设定60个观测值，设定随机数种子

clear all
set obs 60 
set seed 10101
gen id =_n

/// 每一个数值的数量扩大11倍，再减去前六十个观测值，即60*11-60 = 600，为60个体10年的面板数据

expand 11
drop in 1/60
count

///以id分组生成时间标识

bys id: gen time = _n+1999
xtset id time

///生成协变量x1, x2

gen x1 = rnormal(1,7)
gen x2 = rnormal(2,5)

///生成个体固定效应和时间固定效应

sort time id
by time: gen ind = _n
sort id time
by id: gen T = _n

//生成treat和post变量，以2005年为接受政策干预的时点，id为30-60的个体为处理组，其余为控制组

gen D = 0 
replace D = 1 if  id > 29
gen post = 0
replace post = 1 if time >= 2005

///将基础数据结构保存成dta文件，命名为DID_Basic_Simu.dta,默认保存在当前的 working directory 路径下

save "DID_Basic_Simu.dta"，replace

 

连享会计量方法专题……

三、政策效果不随时间而变的 Standard DID 的模拟

///调用本文第二部分生成的基础数据结构
clear
use "DID_Basic_Simu.dta"

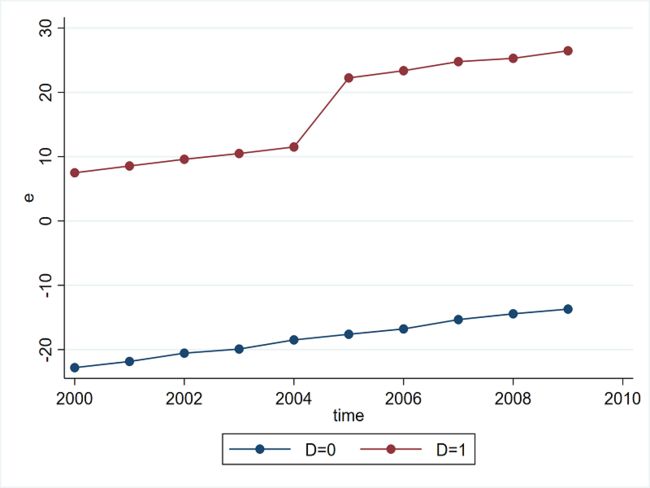
///生成两种潜在结果，并且合成最终的结果变量，令政策的真实效果为10，且不随时间发生变化，直到最后一期

bysort id: gen y0 = 10  + 5 * x1 + 3 * x2 + T + ind + rnormal()
bysort id: gen y1 = 10  + 5 * x1 + 3 * x2 + T + ind + rnormal() if time < 2005
bysort id: replace y1 = 10  + 5 * x1 + 3 * x2 + 10 + T + ind + rnormal() if time >= 2005

gen y = y0 + D * (y1 - y0)

///去除协变量和个体效应对y的影响，画出剩余残差的图像

xtreg y x1 x2 , fe r
predict e,ue
binscatter e time, line(connect) by(D)

///输出生成的图片，令格式为800*600
graph export "article1_1.png",as(png) replace width(800) height(600)
连享会-倍分法DID详解 (一)：传统 DID_第4张图片
图1

利用双向固定效应(two-way fixed effects)的方法估计交互项的系数，其中用到 reg, xtreg, areg, reghdfe 等多个 Stata 命令，四个命令的比较放在了下方的表格中。在本文中，主要展示 reghdfe 命令的输出结果，该命令的具体介绍可以参考 Stata: reghdfe-多维固定效应。

  reg xtreg areg reghdfe
个体固定效应 i.id xtreg,fe areg,absorb(id) absorb(id time)
时间固定效应 i.time i.time i.time absorb(id time)
估计方法 OLS 组内去平均后OLS OLS OLS
优点 命令熟悉，逻辑清晰 固定效应模型的官方命令 官方命令，可以提高组别不随样本规模增加的估计效率 高维固定效应模型，可以极大提到估计效率，且选项多样，如支持多维聚类
缺点 运行速度慢，结果呈现过多不太需要的固定效应的结果 需要手动添加时间固定效应 需要手动添加时间固定效应 无 
reghdfe y c.D#c.post x1 x2, absorb(id time) vce(robust)
+--------------------------------------------------------------------------------+
(converged in 3 iterations)

HDFE Linear regression                                Number of obs   =       600
Absorbing 2 HDFE groups                               F(   3,    528) = 262423.36
Statistics robust to heteroskedasticity               Prob > F        =    0.0000
                                                      R-squared       =    0.9995
                                                      Adj R-squared   =    0.9995  
                                                      Within R-sq.    =    0.9993
                                                      Root MSE        =    1.0154
+-------------------------------------------------------------------------------+       
           |                Robust
         y |      Coef.    Std. Err.     t      P>t     [95% Conf.  Interval]
+-------------------------------------------------------------------------------+       
c.D#c.post |    9.868932   .1654078    59.66    0.000     9.543994  10.19387
        x1 |    4.998123   .0060976   819.69    0.000     4.986144  5.010101
        x2 |    3.003366   .0084909   353.71    0.000     2.986685  3.020046
+-------------------------------------------------------------------------------+
    
Absorbed degrees of freedom:
+--------------------------------------------------------+  
Absorbed FE |  Num. Coefs.  =   Categories  Redundant      
+--------------------------------------------------------+      
        id  |          60              60          0      
      time  |           9              10          1      
+--------------------------------------------------------+

将回归结果存储，并且放在同一张表格中输出。

///四组回归结果输出如下
reg y c.D#c.post x1 x2 i.time i.id, r
eststo reg
xtreg y c.D#c.post x1 x2 i.time, r fe
eststo xtreg_fe
areg y c.D#c.post x1 x2 i.time, absorb(id) robust
eststo areg
reghdfe y c.D#c.post x1 x2, absorb(id time) vce(robust)
eststo reghdfe

estout *, title("The Comparison of Actual Parameter Values") ///
         cells(b(star fmt(%9.3f)) se(par)) ///
         stats(N N_g, fmt(%9.0f %9.0g) label(N Groups)) ///
         legend collabels(none) varlabels(_cons Constant) keep(x1 x2 c.D#c.post)

+--------------------------------------------------------------------------------+
             |             The Comparison of Actual Parameter Values
+--------------------------------------------------------------------------------+      
             |       reg           xtreg_fe      areg       reghdfe   
+--------------------------------------------------------------------------------+      
c.D#c.post   |      9.869***        9.869***    9.869***    9.869***
             |      (0.166)         (0.189)     (0.166)     (0.166)   
x1           |      4.998***        4.998***    4.998***    4.998***
             |      (0.006)         (0.006)     (0.006)     (0.006)   
x2           |      3.003***        3.003***    3.003***    3.003***
             |      (0.008)         (0.008)     (0.008)     (0.008)   
+--------------------------------------------------------------------------------+      
N            |        600             600     600             600   
Groups       |                         60                      
+--------------------------------------------------------------------------------+      
* p<0.05, ** p<0.01, *** p<0.001
+--------------------------------------------------------------------------------+

四组回归结果中交互项和协变量的估计系数和标准误几乎完全相同（唯一的区别在于 xtreg_fe 估计交互项系数的标准差），并且都十分接近于模拟生成时的设定值，说明方程设定和使用的估计方法是合适的。从上面四个回归结果可以知道，交互项的估计系数均为9.86，其95%置信区间明显包含政策的真实效果10。因此，上述四个命令在估计双向固定效应上作用是等价的。

（补充：在本文的模拟中主要使用的是固定效应模型，那么如果使用随机效应模型来估计，方程的形式和结果是否会有变化？这一问题留给感兴趣的读者去思考。PS：仔细观察一下本文的数据生成过程(Data Generating Process, DGP)）。

四、政策效果随时间而变的 Standard DID 的模拟

///调用本文第二部分生成的基础数据结构
clear
use "DID_Basic_Simu.dta"

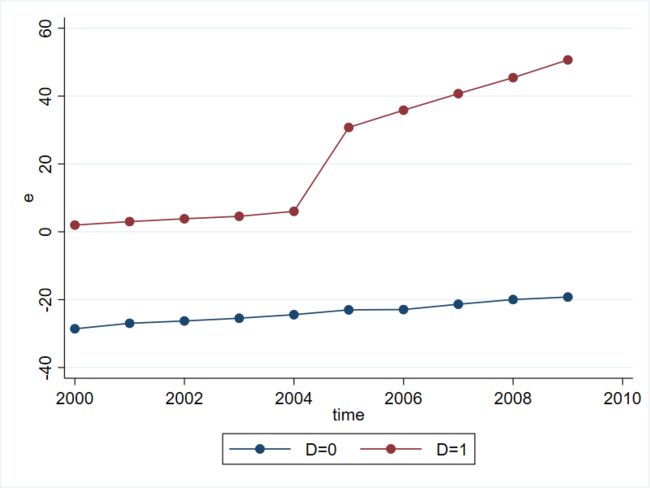
///生成两种潜在结果，并且合成最终的结果变量，令政策的真实效果随时间发生变化，即（5*T-T），由于从2005年开始接受干预，因此，每年的政策效果应为24，28，32，36，40.

bysort id: gen y0 = 10  + 5 * x1 + 3 * x2 + T + ind  + rnormal()
bysort id: gen y1 = 10  + 5 * x1 + 3 * x2 + T + ind  + rnormal() if time < 2005

bysort id: replace y1 = 10  + 5 * x1 + 3 * x2 + T * 5 + ind   + rnormal() if time >= 2005

gen y = y0 + D * (y1 - y0)

///去除协变量和个体效应对y的影响，画出剩余残差的图像

xtreg y x1 x2 , fe r
predict e,ue
binscatter e time, line(connect) by(D)
连享会-倍分法DID详解 (一)：传统 DID_第5张图片
图2

利用双向固定效应(two-way fixed effects)的方法估计交互项的系数，其中用到 reg, xtreg, areg, reghdfe 等多个 Stata 命令。在本文中，主要展示命令'reghdfe'的输出结果。

. reghdfe y c.D#c.post x1 x2, absorb(id time)   vce(robust)
+--------------------------------------------------------------------------------+
(converged in 3 iterations)

HDFE Linear regression                             Number of obs   =           600
Absorbing 2 HDFE groups                            F(   3,    528) =      44552.05
Statistics robust to heteroskedasticity            Prob > F        =        0.0000
                                                   R-squared       =        0.9978
                                                   Adj R-squared   =        0.9975
                                                   Within R-sq.    =        0.9964
                                                   Root MSE        =        2.4029
+--------------------------------------------------------------------------------+      
           |                Robust
         y |      Coef.    Std. Err.      t     P>t     [95% Conf.  Interval]
+--------------------------------------------------------------------------------+  
c.D#c.post |    31.84782   .3931208    81.01    0.000     31.07555  32.6201
        x1 |    5.014706   .0154247   325.11    0.000     4.984405  5.045008
        x2 |    2.973101   .0202111   147.10    0.000     2.933397  3.012805
+--------------------------------------------------------------------------------+
    
Absorbed degrees of freedom:
+-------------------------------------------------------------+ 
Absorbed FE|  Num. Coefs.  =   Categories   Redundant      
+-------------------------------------------------------------+ 
        id |           60              60           0      
      time |            9              10           1      
+-------------------------------------------------------------+

将回归结果存储，并且放在同一张表格中输出。

///四组回归结果输出如下
reg y c.D#c.post x1 x2 i.time i.id, r
eststo reg
xtreg y c.D#c.post x1 x2 i.time, r fe
eststo xtreg_fe
areg y c.D#c.post x1 x2 i.time, absorb(id) robust
eststo areg
reghdfe y c.D#c.post x1 x2, absorb(id time) vce(robust)
eststo reghdfe

estout *, title("The Comparison of Actual Parameter Values") ///
         cells(b(star fmt(%9.3f)) se(par)) ///
         stats(N N_g, fmt(%9.0f %9.0g) label(N Groups)) ///
         legend collabels(none) varlabels(_cons Constant) keep(x1 x2 c.D#c.post)

+--------------------------------------------------------------------------------+
             |             The Comparison of Actual Parameter Values
+--------------------------------------------------------------------------------+      
             |       reg           xtreg_fe       areg          reghdfe   
+--------------------------------------------------------------------------------+      
c.D#c.post   |      31.848***      31.848***     31.848***      31.848***
             |      (0.394)         (0.194)       (0.394)       (0.394)   
x1           |      5.015***       5.015***      5.015***        5.015***
             |      (0.015)         (0.016)       (0.015)       (0.015)   
x2           |      2.973***       2.973***      2.973***        2.973***
             |      (0.020)         (0.019)       (0.020)       (0.020)  
+--------------------------------------------------------------------------------+      
N            |        600             600     600             600   
Groups       |                         60                      
+--------------------------------------------------------------------------------+      
* p<0.05, ** p<0.01, *** p<0.001
+--------------------------------------------------------------------------------+

四组回归结果中交互项和协变量的估计系数和标准误几乎完全相同（唯一的区别在于 xtreg_fe 估计项系数的标准差），并且都十分接近于模拟生成时的设定值，说明方程设定和使用的估计方法是合适的。从上面四个回归结果可以知道，交互项的估计系数均为31.848。再次验证了上述四个命令在估计双向固定效应(two-way fixed effects)上作用是等价的。

（补充：在本文的模拟中主要使用的是固定效应模型，那么如果使用随机效应模型来估计，方程的形式和结果是否会有变化？这一问题留给感兴趣的读者去思考。PS：仔细观察一下本文的数据生成过程(Data Generating Process, DGP)）。

 

连享会计量方法专题……

五、Standard DID 和 Event Study Approach 的结合

本部分介绍政策效果随时间发生变化和不随时间发生变化两种情况下，如何与时间研究法(Event Study Approach)相结合。 DID 应用 ESA 方法有两个目的：一是可以利用回归方法对双重差分法中最重要的平行趋势假设进行检验，与上面的图示法相比，好处在于可以控制协变量的影响，方程形式也更加灵活；二是可以更加清楚地得到政策效果在时间维度上地变化。因此，这部分检验在论文中也往往被称为政策的动态效果(Dynamic Effects) 或者灵活的 DID （Flexible DID Estimates）.具体实现结果如下：

5.1 灵活的 DID ：政策效果不随时间发生变化

Standard DID 的动态效果也有多种语法命令的形式，本文提供两种，主要应用 Stata 的 Factor Variables 语法。

///调用本文第二部分生成的基础数据结构
clear
use "DID_Basic_Simu.dta"

///生成两种潜在结果，并且合成最终的结果变量，令政策的真实效果为10，且不随时间发生变化，直到最后一期

bysort id: gen y0 = 10  + 5 * x1 + 3 * x2 + T + ind + rnormal()
bysort id: gen y1 = 10  + 5 * x1 + 3 * x2 + T + ind + rnormal() if time < 2005
bysort id: replace y1 = 10  + 5 * x1 + 3 * x2 + 10 + T + ind + rnormal() if time >= 2005

gen y = y0 + D * (y1 - y0)

///预先生成年度虚拟变量
tab time, gen(year)

方法1如下：

. reghdfe y i.D#i.time x1 x2, vce(robust) absorb(id time)
+--------------------------------------------------------------------------------+
(converged in 3 iterations)

HDFE Linear regression                                  Number of obs   =      600
Absorbing 2 HDFE groups                                 F(  11,    520) = 71307.67
Statistics robust to heteroskedasticity                 Prob > F        =   0.0000
                                                        R-squared       =   0.9995
                                                        Adj R-squared   =   0.9995
                                                        Within R-sq.    =   0.9993
                                                        Root MSE        =   1.0147

+--------------------------------------------------------------------------------+  
       |               Robust
     y |      Coef.   Std. Err.      t     P>t     [95% Conf.   Interval]
+--------------------------------------------------------------------------------+
D#time |
1 2001 |    .4381916   .3796627     1.15   0.249    -.3076697   1.184053
1 2002 |    .6093975   .3984095     1.53   0.127    -.1732924   1.392087
1 2003 |    .4808495   .3948783     1.22   0.224    -.2949033   1.256602
1 2004 |    .1168801   .4088713     0.29   0.775    -.6863626   .9201227
1 2005 |    9.810181   .3870237    25.35   0.000     9.049859   10.5705
1 2006 |    10.48194   .3664986    28.60   0.000     9.761937   11.20194
1 2007 |    9.999201   .3978656    25.13   0.000     9.217579   10.78082
1 2008 |     10.2474   .4087051    25.07   0.000     9.444481   11.05031
1 2009 |    10.45248   .3979999    26.26   0.000     9.670592   11.23436
    x1 |    4.996797   .0061877   807.54   0.000     4.984641   5.008953
    x2 |    3.004127   .0087679   342.63   0.000     2.986902   3.021352
+--------------------------------------------------------------------------------+
    
Absorbed degrees of freedom:
+-------------------------------------------------------------+     
Absorbed FE|  Num. Coefs.  =   Categories  -   Redundant      
+-------------------------------------------------------------+     
        id |          60              60              0      
      time |           9              10              1      
+-------------------------------------------------------------+

方法2如下：

. reghdfe y c.D#(c.year2-year10) x1 x2, absorb(id time) vce(robust)
+--------------------------------------------------------------------------------+
(converged in 3 iterations)

HDFE Linear regression                                  Number of obs   =      600
Absorbing 2 HDFE groups                                 F(  11,    520) = 71307.67
Statistics robust to heteroskedasticity                 Prob > F        =   0.0000
                                                        R-squared       =   0.9995
                                                        Adj R-squared   =   0.9995
                                                        Within R-sq.    =   0.9993
                                                        Root MSE        =   1.0147
+--------------------------------------------------------------------------------+  
            |               Robust
          y |      Coef.   Std. Err.      t      P>t     [95% Conf. Interval]
+--------------------------------------------------------------------------------+
c.D#c.year2 |    .4381916   .3796627     1.15   0.249    -.3076697  1.184053
c.D#c.year3 |    .6093975   .3984095     1.53   0.127    -.1732924  1.392087
c.D#c.year4 |    .4808495   .3948783     1.22   0.224    -.2949033  1.256602
c.D#c.year5 |    .1168801   .4088713     0.29   0.775    -.6863626  .9201227
c.D#c.year6 |    9.810181   .3870237    25.35   0.000     9.049859  10.5705
c.D#c.year7 |    10.48194   .3664986    28.60   0.000     9.761937  11.20194
c.D#c.year8 |    9.999201   .3978656    25.13   0.000     9.217579  10.78082
c.D#c.year9 |     10.2474   .4087051    25.07   0.000     9.444481  11.05031
c.D#c.year10|    10.45248   .3979999    26.26   0.000     9.670592  11.23436
          x1|    4.996797   .0061877   807.54   0.000     4.984641  5.008953
          x2|    3.004127   .0087679   342.63   0.000     2.986902  3.021352
+--------------------------------------------------------------------------------+
    
Absorbed degrees of freedom:
+-------------------------------------------------------------+     
Absorbed FE|  Num. Coefs.  =   Categories  -   Redundant      
+-------------------------------------------------------------+     
        id |           60              60              0      
      time |            9              10              1      
+-------------------------------------------------------------+

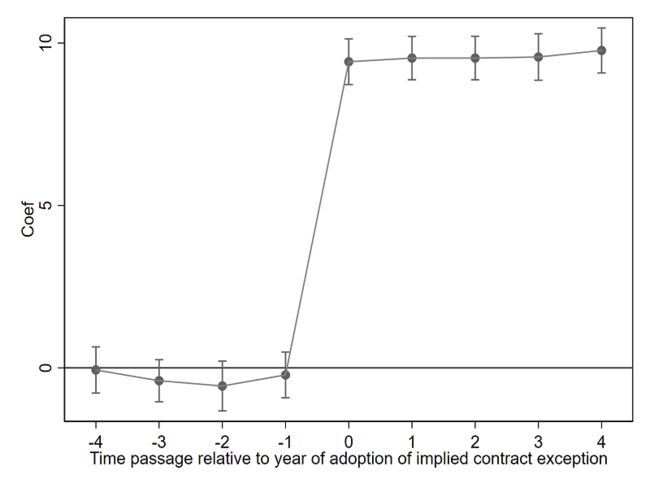
方法1和方法2的主要差异在于：方法2通过手动生成时间虚拟变量，构造出交互项，因此可以指定某一个组别作为参照组，在本文中将样本中的第一期作为基准组，另外在论文中常用的还有讲政策实施的前一期和当期作为基准参照组。除此之外，两种方程设定所得到的估计系数完全一致，以第一期为基期，第二期和第五期的系数的T值远小于2，因此，可以认为它们与0没有显著差异，从而验证了平行趋势假设。第六期到第十期的系数分别是9.81，10.48，9.999，10.25，10.45，其95%CI都包含真实效应10，因此，该方程设定是可靠的。系数的图形化表达如下：

coefplot, ///
   keep(c.D#c.year2 c.D#c.year3 c.D#c.year4 c.D#c.year5 c.D#c.year6 c.D#c.year7 c.D#c.year8 c.D#c.year9 c.D#c.year10)  ///
   coeflabels(c.D#c.year2 = "-4"   ///
   c.D#c.year3 = "-3"           ///
   c.D#c.year4 = "-2"           ///
   c.D#c.year5 = "-1"           ///
   c.D#c.year6  = "0"             ///
   c.D#c.year7  = "1"              ///
   c.D#c.year8  = "2"              ///
   c.D#c.year9  = "3"              ///
   c.D#c.year10 = "4")            ///
   vertical                             ///
   yline(0)                             ///
   ytitle("Coef")                 ///
   xtitle("Time passage relative to year of adoption of implied contract exception") ///
   addplot(line @b @at)                 ///
   ciopts(recast(rcap))                 ///
   scheme(s1mono)
连享会-倍分法DID详解 (一)：传统 DID_第6张图片
图3

5.2 灵活的 DID ： 政策效果随时间发生变化

///调用本文第二部分生成的基础数据结构
clear
use "DID_Basic_Simu.dta"

///生成两种潜在结果，并且合成最终的结果变量，令政策的真实效果随时间发生变化，即（5*T-T），由于从2005年开始接受干预，因此，每年的政策效果应为24，28，32，36，40.

bysort id: gen y0 = 10  + 5 * x1 + 3 * x2 + T + ind  + rnormal()
bysort id: gen y1 = 10  + 5 * x1 + 3 * x2 + T + ind  + rnormal() if time < 2005

bysort id: replace y1 = 10  + 5 * x1 + 3 * x2 + T * 5 + ind   + rnormal() if time >= 2005

gen y = y0 + D * (y1 - y0)

///预先生成年度虚拟变量
tab time, gen(year)

方法1如下：

reghdfe y i.D#i.time x1 x2, vce(robust) absorb(id time)
+--------------------------------------------------------------------------------+
(converged in 3 iterations)

HDFE Linear regression                               Number of obs   =          600
Absorbing 2 HDFE groups                              F(  11,    520) =     75233.93
Statistics robust to heteroskedasticity              Prob > F        =       0.0000
                                                     R-squared       =       0.9996
                                                     Adj R-squared   =       0.9996
                                                     Within R-sq.    =       0.9994
                                                     Root MSE        =       1.0147
+--------------------------------------------------------------------------------+      
       |                   Robust
     y |      Coef.   Std. Err.      t    P>t     [95% Conf.    Interval]
+--------------------------------------------------------------------------------+      
D#time |
1 2001 |    .4381916   .3796627     1.15  0.249    -.3076697    1.184053
1 2002 |    .6093975   .3984095     1.53  0.127    -.1732924    1.392087
1 2003 |    .4808495   .3948783     1.22  0.224    -.2949033    1.256602
1 2004 |    .1168801   .4088713     0.29  0.775    -.6863626    .9201227
1 2005 |    23.81018   .3870237    61.52  0.000     23.04986    24.5705
1 2006 |    28.48194   .3664986    77.71  0.000     27.76194    29.20194
1 2007 |    31.9992    .3978656    80.43  0.000     31.21758    32.78082
1 2008 |    36.2474    .4087051    88.69  0.000     35.44448    37.05031
1 2009 |    40.45248   .3979999   101.64  0.000     39.67059    41.23436
+--------------------------------------------------------------------------------+
    x1 |    4.996797   .0061877   807.54  0.000     4.984641    5.008953
    x2 |    3.004127   .0087679   342.63  0.000     2.986902    3.021352
+--------------------------------------------------------------------------------+
         

Absorbed degrees of freedom:
+-------------------------------------------------------------+     
Absorbed FE|   Num. Coefs.  =   Categories  Redundant      
+-------------------------------------------------------------+     
        id |          60              60            0      
      time |           9              10            1      
+-------------------------------------------------------------+ 

reghdfe y c.D#(c.year2-year10) x1 x2 , absorb(id time) vce(robust)
+--------------------------------------------------------------------------------+      
(converged in 3 iterations)

HDFE Linear regression                                  Number of obs   =      600
Absorbing 2 HDFE groups                                 F(  11,    520) = 75233.93
Statistics robust to heteroskedasticity                 Prob > F        =   0.0000
                                                        R-squared       =   0.9996
                                                        Adj R-squared   =   0.9996
                                                        Within R-sq.    =   0.9994
                                                        Root MSE        =   1.0147
+--------------------------------------------------------------------------------+              
            |              Robust
          y |     Coef.   Std. Err.      t      P>t     [95% Conf.  Interval]       
+--------------------------------------------------------------------------------+      
c.D#c.year2 |   .4381916   .3796627     1.15    0.249    -.3076697  1.184053
c.D#c.year3 |   .6093975   .3984095     1.53    0.127    -.1732924  1.392087
c.D#c.year4 |   .4808495   .3948783     1.22    0.224    -.2949033  1.256602
c.D#c.year5 |   .1168801   .4088713     0.29    0.775    -.6863626  .9201227
c.D#c.year6 |   23.81018   .3870237    61.52    0.000     23.04986  24.5705
c.D#c.year7 |   28.48194   .3664986    77.71    0.000     27.76194  29.20194
c.D#c.year8 |   31.9992   .3978656     80.43    0.000     31.21758  32.78082
c.D#c.year9 |   36.2474   .4087051     88.69    0.000     35.44448  37.05031
c.D#c.year10|   40.45248   .3979999   101.64    0.000     39.67059  41.23436
          x1|   4.996797   .0061877   807.54    0.000     4.984641  5.008953
          x2|   3.004127   .0087679   342.63    0.000     2.986902  3.021352
+--------------------------------------------------------------------------------+      
        

Absorbed degrees of freedom:
+-------------------------------------------------------------+         
Absorbed FE|   Num. Coefs.  =   Categories  Redundant      
+-------------------------------------------------------------+     
        id |          60              60            0      
      time |           9              10            1      
+-------------------------------------------------------------+

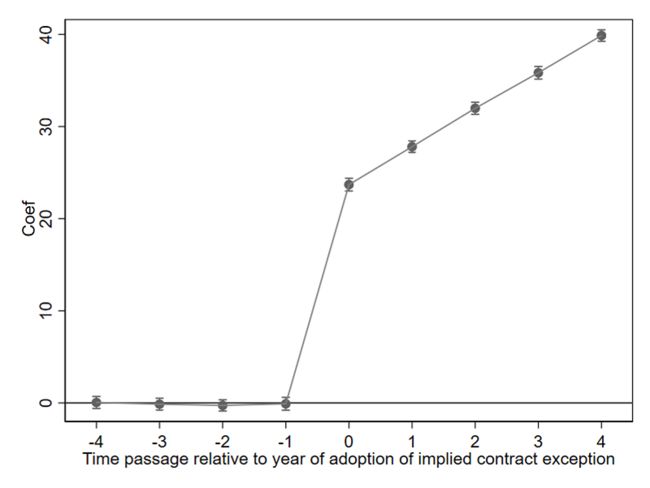
上面两种方法的估计结果完全一致，前五期的T值远小于2，因此可以认为这些估计系数与0无显著差异，而且从第六期开始，估计系数分别为23.81，28.48，32.00，36.25，40.45,这与模拟程序设定的真实值十分接近。下一步是将回归方程的结果通过图形更加直观的呈现出来，具体如下：

coefplot, ///
   keep(c.D#c.year2 c.D#c.year3 c.D#c.year4 c.D#c.year5 c.D#c.year6 c.D#c.year7 c.D#c.year8 c.D#c.year9 c.D#c.year10)  ///
   coeflabels(c.D#c.year2 = "-4"   ///
   c.D#c.year3 = "-3"           ///
   c.D#c.year4 = "-2"           ///
   c.D#c.year5 = "-1"           ///
   c.D#c.year6  = "0"             ///
   c.D#c.year7  = "1"              ///
   c.D#c.year8  = "2"              ///
   c.D#c.year9  = "3"              ///
   c.D#c.year10 = "4")            ///
   vertical                             ///
   yline(0)                             ///
   ytitle("Coef")                 ///
   xtitle("Time passage relative to year of adoption of implied contract exception") ///
   addplot(line @b @at)                 ///
   ciopts(recast(rcap))                 ///
   scheme(s1mono)
连享会-倍分法DID详解 (一)：传统 DID_第7张图片
图4

六、总结和拓展

本文是本系列推文的第一篇，其主要内容是介绍了政策效果不随时间而变和政策效果随时间而变的 DID 模型的模拟，结合 Event Study Approach
对 DID 最重要的平行趋势假设进行了检验，另外利用 coefplot 命令对 DID 方法所估计的政策动态效果进行了图形化展示。

本系列的下一篇推文将介绍 Time-varying DID 的模拟，平行趋势检验在不同情形下的模型设定的差异以及政策动态效果的图形化表达。

参考资料

  1. Stata: 双重差分的固定效益模型
  2. 多期DID：平行趋势检验图示
  3. DID 边际分析：让政策评价结果更加丰满
  4. 双重差分模型的平行趋势假定如何检验？ ——coefplot命令来告诉你（一）
  5. 双重差分模型的平行趋势假定如何检验？ ——coefplot命令来告诉你（二）
  6. 模型系列-DID入门(附Stata操作)
  7. Stata: reghdfe-多维固定效应
  8. 开学礼包：如何使用双重差分法的交叉项（迄今最全攻略）

附：全部代码

基础数据结构的生成和保存

///设定60个观测值，设定随机数种子

clear all
set obs 60 
set seed 10101
gen id =_n

/// 每一个数值的数量扩大11倍，再减去前六十个观测值，即60*11-60 = 600，为60个体10年的面板数据

expand 11
drop in 1/60
count

///以id分组生成时间标识

bys id: gen time = _n+1999
xtset id time

///生成协变量x1, x2

gen x1 = rnormal(1,7)
gen x2 = rnormal(2,5)

///生成个体固定效应和时间固定效应

sort time id
by time: gen ind = _n
sort id time
by id: gen T = _n

///生成treat和post变量，以2005年为接受政策干预的时点，id为30-60的个体为处理组，其余为控制组

gen D = 0 
replace D = 1 if  id > 29
gen post = 0
replace post = 1 if time >= 2005

///将基础数据结构保存成dta文件，命名为DID_Basic_Simu.dta,默认保存在当前的 working directory 路径下

save "DID_Basic_Simu.dta"，replace

政策效果不随时间而变DID模拟的代码

///调用本文第二部分生成的基础数据结构
clear
use "DID_Basic_Simu.dta"

///生成两种潜在结果，并且合成最终的结果变量，令政策的真实效果为10

bysort id: gen y0 = 10  + 5 * x1 + 3 * x2 + T + ind  + rnormal()
bysort id: gen y1 = 10  + 5 * x1 + 3 * x2 + T + ind  + rnormal() if time < 2005

bysort id: replace y1 = 10  + 5 * x1 + 3 * x2 + 10 + T + ind  + rnormal() if time >= 2005

gen y = y0 + D * (y1 - y0)

///去除协变量和个体效应对y的影响，画出剩余残差的图像

xtreg y x1 x2 , fe r
predict e,ue
binscatter e time, line(connect) by(D)

///输出生成的图片，令格式为800*600
graph export "article1_1.png",as(png) replace width(800) height(600)

///多种回归形式
reg y c.D#c.post x1 x2 i.time i.id, r
eststo reg
xtreg y c.D#c.post x1 x2 i.time, r fe
eststo xtreg_fe
areg y c.D#c.post x1 x2 i.time, absorb(id) robust
eststo areg
reghdfe y c.D#c.post x1 x2, absorb(id time) vce(robust)
eststo reghdfe

estout *, title("The Comparison of Actual Paramerer Values") ///
         cells(b(star fmt(%9.3f)) se(par)) ///
         stats(N N_g, fmt(%9.0f %9.0g) label(N Groups)) ///
         legend collabels(none) varlabels(_cons Constant) keep(x1 x2 c.D#c.post)

///ESA及图示法
///预先生成年度虚拟变量
tab time, gen(year)
reghdfe y i.D#i.time x1 x2, vce(robust) absorb(id time)
reghdfe y c.D#(c.year2-year10) x1 x2, absorb(id time) vce(robust)
coefplot, ///
   keep(c.D#c.year2 c.D#c.year3 c.D#c.year4 c.D#c.year5 c.D#c.year6 c.D#c.year7 c.D#c.year8 c.D#c.year9 c.D#c.year10)  ///
   coeflabels(c.D#c.year2 = "-4"   ///
   c.D#c.year3 = "-3"           ///
   c.D#c.year4 = "-2"           ///
   c.D#c.year5 = "-1"           ///
   c.D#c.year6  = "0"             ///
   c.D#c.year7  = "1"              ///
   c.D#c.year8  = "2"              ///
   c.D#c.year9  = "3"              ///
   c.D#c.year10 = "4")            ///
   vertical                             ///
   yline(0)                             ///
   ytitle("Coef")                 ///
   xtitle("Time passage relative to year of adoption of implied contract exception") ///
   addplot(line @b @at)                 ///
   ciopts(recast(rcap))                 ///
   scheme(s1mono)

 ///输出生成的图片，令格式为800*600
 graph export "article1_3.png",as(png) replace width(800) height(600)

政策效果随时间而变DID模拟的代码

///调用本文第二部分生成的基础数据结构
clear
use "DID_Basic_Simu.dta"

///生成两种潜在结果，并且合成最终的结果变量，令政策的真实效果随时间发生变化，即（5*T-T），由于从2005年开始接受干预，因此，每年的政策效果应为24，28，32，36，40.

bysort id: gen y0 = 10  + 5 * x1 + 3 * x2 + T + ind  + rnormal()
bysort id: gen y1 = 10  + 5 * x1 + 3 * x2 + T + ind  + rnormal() if time < 2005

bysort id: replace y1 = 10  + 5 * x1 + 3 * x2 + T * 5 + ind   + rnormal() if time >= 2005

gen y = y0 + D * (y1 - y0)

///去除协变量和个体效应对y的影响，画出剩余残差的图像

xtreg y x1 x2 , fe r
predict e,ue
binscatter e time, line(connect) by(D)

///输出生成的图片，令格式为800*600
graph export "article1_2.png",as(png) replace width(800) height(600)

///多种回归形式
reg y c.D#c.post x1 x2 i.time i.id, r
eststo reg
xtreg y c.D#c.post x1 x2 i.time, r fe
eststo xtreg_fe
areg y c.D#c.post x1 x2 i.time, absorb(id) robust
eststo areg
reghdfe y c.D#c.post x1 x2, absorb(id time) vce(robust)
eststo reghdfe

estout *, title("The Comparison of Actual Paramerer Values") ///
         cells(b(star fmt(%9.3f)) se(par)) ///
         stats(N N_g, fmt(%9.0f %9.0g) label(N Groups)) ///
         legend collabels(none) varlabels(_cons Constant) keep(x1 x2 c.D#c.post)

///ESA及图示法
///预先生成年度虚拟变量
tab time, gen(year)
reghdfe y i.D#i.time x1 x2, vce(robust) absorb(id time)
reghdfe y c.D#(c.year2-year10) x1 x2, absorb(id time) vce(robust)
coefplot, ///
   keep(c.D#c.year2 c.D#c.year3 c.D#c.year4 c.D#c.year5 c.D#c.year6 c.D#c.year7 c.D#c.year8 c.D#c.year9 c.D#c.year10)  ///
   coeflabels(c.D#c.year2 = "-4"   ///
   c.D#c.year3 = "-3"           ///
   c.D#c.year4 = "-2"           ///
   c.D#c.year5 = "-1"           ///
   c.D#c.year6  = "0"             ///
   c.D#c.year7  = "1"              ///
   c.D#c.year8  = "2"              ///
   c.D#c.year9  = "3"              ///
   c.D#c.year10 = "4")            ///
   vertical                             ///
   yline(0)                             ///
   ytitle("Coef")                 ///
   xtitle("Time passage relative to year of adoption of implied contract exception") ///
   addplot(line @b @at)                 ///
   ciopts(recast(rcap))                 ///
   scheme(s1mono)

 ///输出生成的图片，令格式为800*600
 graph export "article1_4.png",as(png) replace width(800) height(600)

 

 

关于我们

  • 「Stata 连享会」 由中山大学连玉君老师团队创办，定期分享实证分析经验， 公众号：StataChina。
  • 公众号推文同步发布于 CSDN 、 和 知乎Stata专栏。可在百度中搜索关键词 「Stata连享会」查看往期推文。
  • 点击推文底部【阅读原文】可以查看推文中的链接并下载相关资料。
  • 欢迎赐稿： 欢迎赐稿。录用稿件达 三篇 以上，即可 免费 获得一期 Stata 现场培训资格。
  • E-mail： [email protected]
  • 往期推文：计量专题 || 精品课程 || 推文 || 公众号合集

连享会-倍分法DID详解 (一)：传统 DID_第8张图片
点击查看完整推文列表

连享会-倍分法DID详解 (一)：传统 DID_第9张图片
欢迎加入Stata连享会(公众号: StataChina)

你可能感兴趣的:(连享会-倍分法DID详解 (一)：传统 DID)

  • 斤斤计较的婚姻到底有多难？ 白心之岂必有为
    很多人私聊我会问到在哪个人群当中斤斤计较的人最多？我都会回答他，一般婚姻出现问题的斤斤计较的人士会非常多，以我多年经验，在婚姻落的一塌糊涂的人当中，斤斤计较的人数占比在20～30%以上，也就是说10个婚姻出现问题的斤斤计较的人有2-3个有多不减。在婚姻出问题当中，有大量的心理不平衡的、尖酸刻薄的怨妇。在婚姻中仅斤斤计较有两种类型：第一种是物质上的，另一种是精神上的。在物质与精神上抠门已经严重的影响
  • 情绪觉察日记第37天 露露_e800
    今天是家庭关系规划师的第二阶最后一天，慧萍老师帮我做了个案，帮我处理了埋在心底好多年的一份恐惧，并给了我深深的力量！这几天出来学习，爸妈过来婆家帮我带小孩，妈妈出于爱帮我收拾东西，并跟我先生和婆婆产生矛盾，妈妈觉得他们没有照顾好我…。今晚回家见到妈妈，我很欣赏她并赞扬她，妈妈说今晚要跟我睡我说好，当我们俩躺在床上准备睡觉的时候，我握着妈妈的手对她说:妈妈这几天辛苦你了，你看你多利害把我们的家收拾得
  • 芦花鞋一四 许叶晗
    又是在一个寒冷的夏日里，青铜和葵花决定今天一起去卖芦花鞋，奶奶亲手给他们做了一碗热乎乎的粥对他们说:“就靠你们两挣生活费了这碗粥赶紧趁热喝了吧！”于是青铜和葵花喝完了奶奶给她们做的粥，就准备去镇上卖卢花鞋，这回青铜和葵花穿着新的芦花鞋来到了镇上。青铜这回看到了很多人都在卖，用手势表达对葵花说:“这回有好多人在抢我们生意呢！我们必须得吆喝起来。”葵花点了点头。可是谁知他们也大声的叫，卖芦花喽！卖芦花
  • QQ群采集助手，精准引流必备神器 2401_87347160 其他经验分享
    功能概述微信群查找与筛选工具是一款专为微信用户设计的辅助工具，它通过关键词搜索功能，帮助用户快速找到相关的微信群，并提供筛选是否需要验证的群组的功能。主要功能关键词搜索：用户可以输入关键词，工具将自动查找包含该关键词的微信群。筛选功能：工具提供筛选机制，用户可以选择是否只显示需要验证或不需要验证的群组。精准引流：通过上述功能，用户可以更精准地找到目标群组，进行有效的引流操作。3.设备需求该工具可以
  • 机器学习与深度学习间关系与区别 ℒℴѵℯ心·动ꦿ໊ོ꫞ 人工智能学习深度学习python
    一、机器学习概述定义机器学习（MachineLearning,ML）是一种通过数据驱动的方法，利用统计学和计算算法来训练模型，使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本，识别其中的模式和规律，从而对新的数据进行判断。其核心在于通过训练过程，让模型不断优化和提升其预测准确性。主要类型1.监督学习（SupervisedLearning）监督学习是指在训练数据集中包含输入
  • 铭刻于星（四十二） 随风至
    69夜晚，绍敏同学做完功课后，看了眼房外，没听到动静才敢从书包的夹层里拿出那个心形纸团。折痕压得很深，都有些旧了，想来是已经写好很久了。绍敏同学慢慢地、轻轻地捏开折叠处，待到全部拆开后，又反复抚平纸张，然后仔细地一字字默看。只是开头的三个字是第一次看到，让她心漏跳了几拍。“亲爱的绍敏：从四年级的时候，我就喜欢你了，但是我一直不敢说，怕影响你学习。六年级的时候听说有人跟你表白，你接受了，我很难过，但
  • 底层逆袭到底有多难，不甘平凡的你准备好了吗？让吴起给你说说 造命者说
    底层逆袭到底有多难，不甘平凡的你准备好了吗？让吴起给你说说我叫吴起，生于公元前440年的战国初期，正是群雄并起、天下纷争不断的时候。后人说我是军事家、政治家、改革家，是兵家代表人物。评价我一生历仕鲁、魏、楚三国，通晓兵家、法家、儒家三家思想，在内政军事上都有极高的成就。周安王二十一年（公元前381年），因变法得罪守旧贵族，被人乱箭射死。我出生在卫国一个“家累万金”的富有家庭，从年轻时候起就不甘平凡
  • 2020-01-25 晴岚85
    郑海燕坚持分享590天2020.1.24在生活中只存在两个问题。一个问题是：你知道想要达成的目标是什么，但却不知道如何才能达成；另一个问题是：你不知道你的目标是什么。前一个是行动的问题，后一个是结果的问题。通过制定具体的下一步行动，可以解决不知道如何开始行动的问题。而通过去想象结果，对结果做预估，可以解决找不着目标的问题。对于所有吸引我们注意力，想要完成的任务，你可以先想象一下，预期的结果究竟是什
  • 随笔 | 仙一般的灵气 海思沧海
    仙岛今天，我看了你全部，似乎已经进入你的世界我不知道，这是否是梦幻，还是你仙一般的灵气吸引了我也许每一个人都要有一份属于自己的追求，这样才能够符合人生的梦想，生活才能够充满着阳光与快乐我不知道，我为什么会这样的感叹，是在感叹自己的人生，还是感叹自己一直没有孜孜不倦的追求只感觉虚度了光阴，每天活在自己的梦中，活在一个不真实的世界是在逃避自己，还是在逃避周围的一切有时候我嘲笑自己，嘲笑自己如此的虚无，
  • 想家 爆米花机
    也许不同于大家对家乡的思念，我对家乡甚至是疯狂的不舍。还未踏出车站就感觉到幸福，我享受这里的夕阳、这里的浓烈柴火味、这里每一口家常菜。我是宅女，我贪恋家的安逸。刚刚踏出大学校门，初出茅庐，无法适应每年只能国庆和春节回家。我焦虑、失眠、无端发脾气，是无法适应工作的节奏，是无法接受我将一步步离开家乡的事实。我不想承认自己胸无大志，选择再次踏上征程。图片发自App
  • 【iOS】MVC设计模式 Magnetic_h iosmvc设计模式objective-c学习ui
    MVC前言如何设计一个程序的结构，这是一门专门的学问，叫做"架构模式"（architecturalpattern），属于编程的方法论。MVC模式就是架构模式的一种。它是Apple官方推荐的App开发架构，也是一般开发者最先遇到、最经典的架构。MVC各层controller层Controller/ViewController/VC（控制器）负责协调Model和View，处理大部分逻辑它将数据从Mod
  • OC语言多界面传值五大方式 Magnetic_h iosui学习objective-c开发语言
    前言在完成暑假仿写项目时，遇到了许多需要用到多界面传值的地方，这篇博客来总结一下比较常用的五种多界面传值的方式。属性传值属性传值一般用前一个界面向后一个界面传值，简单地说就是通过访问后一个视图控制器的属性来为它赋值，通过这个属性来做到从前一个界面向后一个界面传值。首先在后一个界面中定义属性@interfaceBViewController:UIViewController@propertyNSSt
  • 一百九十四章. 自相矛盾 巨木擎天
    唉！就这么一夜，林子感觉就像过了很多天似的，先是回了阳间家里，遇到了那么多不可思议的事情儿。特别是小伙伴们，第二次与自己见面时，僵硬的表情和恐怖的气氛，让自己如坐针毡，打从心眼里难受！还有东子，他现在还好吗？有没有被人欺负？护城河里的小鱼小虾们，还都在吗？水不会真的干枯了吧？那对相亲相爱漂亮的太平鸟儿，还好吧！春天了，到了做窝、下蛋、喂养小鸟宝宝的时候了，希望它们都能够平安啊！虽然没有看见家人，也
  • UI学习——cell的复用和自定义cell Magnetic_h ui学习
    目录cell的复用手动（非注册）自动（注册）自定义cellcell的复用在iOS开发中，单元格复用是一种提高表格（UITableView）和集合视图（UICollectionView）滚动性能的技术。当一个UITableViewCell或UICollectionViewCell首次需要显示时，如果没有可复用的单元格，则视图会创建一个新的单元格。一旦这个单元格滚动出屏幕，它就不会被销毁。相反，它被添
  • element实现动态路由+面包屑 软件技术NINI vue案例vue.js前端
    el-breadcrumb是ElementUI组件库中的一个面包屑导航组件，它用于显示当前页面的路径，帮助用户快速理解和导航到应用的各个部分。在Vue.js项目中，如果你已经安装了ElementUI，就可以很方便地使用el-breadcrumb组件。以下是一个基本的使用示例：安装ElementUI（如果你还没有安装的话）:你可以通过npm或yarn来安装ElementUI。bash复制代码npmi
  • 10月|愿你的青春不负梦想-读书笔记-01 Tracy的小书斋
    本书的作者是俞敏洪，大家都很熟悉他了吧。俞敏洪老师是我行业的领头羊吧，也是我事业上的偶像。本日摘录他书中第一章中的金句：『一个人如果什么目标都没有，就会浑浑噩噩，感觉生命中缺少能量。能给我们能量的，是对未来的期待。第一件事，我始终为了进步而努力。与其追寻全世界的骏马，不如种植丰美的草原，到时骏马自然会来。第二件事，我始终有阶段性的目标。什么东西能给我能量？答案是对未来的期待。』读到这里的时候，我便
  • C语言宏函数 南林yan C语言c语言
    一、什么是宏函数？通过宏定义的函数是宏函数。如下，编译器在预处理阶段会将Add(x,y)替换为((x)*(y))#defineAdd(x,y)((x)*(y))#defineAdd(x,y)((x)*(y))intmain(){inta=10;intb=20;intd=10;intc=Add(a+d,b)*2;cout<
  • 地推话术，如何应对地推过程中家长的拒绝 校师学
    相信校长们在做地推的时候经常遇到这种情况：市场专员反馈家长不接单，咨询师反馈难以邀约这些家长上门，校区地推疲软，招生难。为什么？仅从地推层面分析，一方面因为家长受到的信息轰炸越来越多，对信息越来越“免疫”；而另一方面地推人员的专业能力和营销话术没有提高，无法应对家长的拒绝，对有意向的家长也不知如何跟进，眼睁睁看着家长走远；对于家长的疑问，更不知道如何有技巧地回答，机会白白流失。由于回答没技巧和专业
  • 谢谢你们，爱你们！ 鹿游儿
    昨天家人去泡温泉，二个孩子也带着去，出发前一晚，匆匆下班，赶回家和孩子一起收拾。饭后，我拿出笔和本子（上次去澳门时做手帐的本子）写下了1\2\3\4\5\6\7\8\9,让后让小壹去思考，带什么出发去旅游呢？她在对应的数字旁边画上了，泳衣、泳圈、肖恩、内衣内裤、tapuy、拖鞋……画完后，就让她自己对着这个本子，将要带的，一一带上，没想到这次带的书还是这本《便便工厂》(晚上姑婆发照片过来，妹妹累得
  • C语言如何定义宏函数？ 小九格物 c语言
    在C语言中，宏函数是通过预处理器定义的，它在编译之前替换代码中的宏调用。宏函数可以模拟函数的行为，但它们不是真正的函数，因为它们在编译时不会进行类型检查，也不会分配存储空间。宏函数的定义通常使用#define指令，后面跟着宏的名称和参数列表，以及宏展开后的代码。宏函数的定义方式：1.基本宏函数：这是最简单的宏函数形式，它直接定义一个表达式。#defineSQUARE(x)((x)*(x))2.带参
  • 理解Gunicorn：Python WSGI服务器的基石 范范0825 ipythonlinux运维
    理解Gunicorn：PythonWSGI服务器的基石介绍Gunicorn，全称GreenUnicorn，是一个为PythonWSGI（WebServerGatewayInterface）应用设计的高效、轻量级HTTP服务器。作为PythonWeb应用部署的常用工具，Gunicorn以其高性能和易用性著称。本文将介绍Gunicorn的基本概念、安装和配置，帮助初学者快速上手。1.什么是Gunico
  • 小丽成长记（四十三） 玲玲54321
    小丽发现，即使她好不容易调整好自己的心态下一秒总会有不确定的伤脑筋的事出现，一个接一个的问题，人生就没有停下的时候，小问题不断出现。不过她今天看的书，她接受了人生就是不确定的，厉害的人就是不断创造确定性，在Ta的领域比别人多的确定性就能让自己脱颖而出，显示价值从而获得的比别人多的利益。正是这样的原因，因为从前修炼自己太少，使得她现在在人生道路上打怪起来困难重重，她似乎永远摆脱不了那种无力感，有种习
  • 学点心理知识，呵护孩子健康 静候花开_7090
    昨天听了华中师范大学教育管理学系副教授张玲老师的《哪里才是学生心理健康的最后庇护所，超越教育与技术的思考》的讲座。今天又重新学习了一遍，收获匪浅。张玲博士也注意到了当今社会上的孩子由于心理问题导致的自残、自杀及伤害他人等恶性事件。她向我们普及了一个重要的命题，她说心理健康的一些基本命题，我们与我们通常的一些教育命题是不同的，她还举了几个例子，让我们明白我们原来以为的健康并非心理学上的健康。比如如果
  • 2021年12月19日，春蕾教育集团团建活动感受——黄晓丹 黄错错加油
    感受:1.从陌生到熟悉的过程。游戏环节让我们在轻松的氛围中得到了锻炼，也增长了不少知识。2.游戏过程中，我们贡献的是个人力量，展现的是团队的力量。它磨合的往往不止是工作的熟悉，更是观念上契合度的贴近。3.这和工作是一样的道理。在各自的岗位上，每个人摆正自己的位置、各司其职充分发挥才能，并团结一致劲往一处使，才能实现最大的成功。新知:1.团队精神需要不断地创新。过去，人们把创新看作是冒风险，现在人们
  • Cell Insight | 单细胞测序技术又一新发现，可用于HIV-1和Mtb共感染个体诊断 尐尐呅
    结核病是艾滋病合并其他疾病中导致患者死亡的主要原因。其中结核病由结核分枝杆菌（Mycobacteriumtuberculosis,Mtb）感染引起，获得性免疫缺陷综合症（艾滋病）由人免疫缺陷病毒（Humanimmunodeficiencyvirustype1,HIV-1）感染引起。国家感染性疾病临床医学研究中心/深圳市第三人民医院张国良团队携手深圳华大生命科学研究院吴靓团队，共同研究得出单细胞测序
  • 瑶池防线 谜影梦蝶
    冥华虽然逃过了影梦的军队，但他是一个忠臣，他选择上报战况。败给影梦后成逃兵，高层亡尔还活着，七重天失守......随便一条，即可处死冥华。冥华自然是知道以仙界高层的习性此信一发自己必死无疑，但他还选择上报实情，因为责任。同样此信送到仙宫后，知道此事的人，大多数人都认定冥华要完了，所以上到仙界高层，下到扫大街的，包括冥华自己，全都准备好迎接冥华之死。如果仙界现在还属于两方之争的话，冥华必死无疑。然而
  • 爬山后遗症 璃绛
    爬山，攀登，一步一步走向制高点，是一种挑战。成功抵达是一种无法言语的快乐，在山顶吹吹风，看看风景，这是从未有过的体验。然而，爬山一时爽，下山腿打颤，颠簸的路，一路向下走，腿部力量不够，走起来抖到不行，停不下来了！第二天必定腿疼，浑身酸痛，坐立难安！
  • 《投行人生》读书笔记 小蘑菇的树洞
    《投行人生》----作者詹姆斯-A-朗德摩根斯坦利副主席40年的职业洞见-很短小精悍的篇幅，比较适合初入职场的新人。第一部分成功的职业生涯需要规划1.情商归为适应能力分享与协作同理心适应能力，更多的是自我意识，你有能力识别自己的情并分辨这些情绪如何影响你的思想和行为。2.对于初入职场的人的建议，细节，截止日期和数据很重要截止日期，一种有效的方法是请老板为你所有的任务进行优先级排序。和老板喝咖啡的好
  • 《策划经理回忆录之二》 路基雅虎
    话说三年变六年，飘了，飘了……眨眼，2013年5月，老吴回到了他的家乡——油城从新开启他的工作幻想症生涯。很庆幸，这是一家很有追求，同时敢于尝试的，且实力不容低调的新星房企——金源置业(前身泰源置业)更值得庆幸的是第一个盘就是油城十路的标杆之一:金源盛世。2013年5月，到2015年11月，两年的陪伴，迎来了一场大爆发。2000个筹，5万/筹，直接回笼1个亿！！！这……让我开始认真审视这座看似五线
  • Long类型前后端数据不一致 igotyback 前端
    响应给前端的数据浏览器控制台中response中看到的Long类型的数据是正常的到前端数据不一致前后端数据类型不匹配是一个常见问题，尤其是当后端使用Java的Long类型（64位）与前端JavaScript的Number类型（最大安全整数为2^53-1，即16位）进行数据交互时，很容易出现精度丢失的问题。这是因为JavaScript中的Number类型无法安全地表示超过16位的整数。为了解决这个问
  • java封装继承多态等 麦田的设计者 javaeclipsejvmcencapsulatopn
           最近一段时间看了很多的视频却忘记总结了，现在只能想到什么写什么了，希望能起到一个回忆巩固的作用。     1、final关键字       译为：最终的        &
  • F5与集群的区别 bijian1013 weblogic集群F5
            http请求配置不是通过集群，而是F5；集群是weblogic容器的，如果是ejb接口是通过集群。         F5同集群的差别，主要还是会话复制的问题，F5一把是分发http请求用的，因为http都是无状态的服务，无需关注会话问题，类似
  • LeetCode[Math] - #7 Reverse Integer Cwind java题解MathLeetCodeAlgorithm
    原题链接：#7 Reverse Integer   要求： 按位反转输入的数字 例1： 输入 x = 123, 返回 321 例2： 输入 x = -123, 返回 -321   难度：简单   分析： 对于一般情况，首先保存输入数字的符号，然后每次取输入的末位（x%10）作为输出的高位（result = result*10 + x%10）即可。但
  • BufferedOutputStream 周凡杨
         首先说一下这个大批量，是指有上千万的数据量。      例子：      有一张短信历史表，其数据有上千万条数据，要进行数据备份到文本文件，就是执行如下SQL然后将结果集写入到文件中！      select t.msisd
  • linux下模拟按键输入和鼠标 被触发 linux
    查看/dev/input/eventX是什么类型的事件， cat /proc/bus/input/devices 设备有着自己特殊的按键键码，我需要将一些标准的按键，比如0－9，X－Z等模拟成标准按键，比如KEY_0,KEY-Z等，所以需要用到按键 模拟，具体方法就是操作/dev/input/event1文件，向它写入个input_event结构体就可以模拟按键的输入了。 linux/in
  • ContentProvider初体验 肆无忌惮_ ContentProvider
    ContentProvider在安卓开发中非常重要。与Activity，Service，BroadcastReceiver并称安卓组件四大天王。 在android中的作用是用来对外共享数据。因为安卓程序的数据库文件存放在data/data/packagename里面，这里面的文件默认都是私有的，别的程序无法访问。 如果QQ游戏想访问手机QQ的帐号信息一键登录，那么就需要使用内容提供者COnte
  • 关于Spring MVC项目（maven）中通过fileupload上传文件 843977358 mybatisspring mvc修改头像上传文件upload
    Spring MVC 中通过fileupload上传文件，其中项目使用maven管理。   1.上传文件首先需要的是导入相关支持jar包：commons-fileupload.jar,commons-io.jar 因为我是用的maven管理项目，所以要在pom文件中配置（每个人的jar包位置根据实际情况定） <!-- 文件上传 start by zhangyd-c --&g
  • 使用svnkit api，纯java操作svn，实现svn提交，更新等操作 aigo svnkit
     原文：http://blog.csdn.net/hardwin/article/details/7963318   import java.io.File; import org.apache.log4j.Logger; import org.tmatesoft.svn.core.SVNCommitInfo; import org.tmateso
  • 对比浏览器，casperjs，httpclient的Header信息 alleni123 爬虫crawlerheader
    @Override protected void doGet(HttpServletRequest req, HttpServletResponse res) throws ServletException, IOException { String type=req.getParameter("type"); Enumeration es=re
  • java.io操作 DataInputStream和DataOutputStream基本数据流 百合不是茶 java流
    1，java中如果不保存整个对象，只保存类中的属性，那么我们可以使用本篇文章中的方法，如果要保存整个对象  先将类实例化  后面的文章将详细写到     2，DataInputStream 是java.io包中一个数据输入流允许应用程序以与机器无关方式从底层输入流中读取基本 Java 数据类型。应用程序可以使用数据输出流写入稍后由数据输入流读取的数据。
  • 车辆保险理赔案例 bijian1013 车险
    理赔案例： 一货运车，运输公司为车辆购买了机动车商业险和交强险，也买了安全生产责任险，运输一车烟花爆竹，在行驶途中发生爆炸，出现车毁、货损、司机亡、炸死一路人、炸毁一间民宅等惨剧，针对这几种情况，该如何赔付。 赔付建议和方案： 客户所买交强险在这里不起作用，因为交强险的赔付前提是：“机动车发生道路交通意外事故”； 如果是交通意外事故引发的爆炸，则优先适用交强险条款进行赔付，不足的部分由商业
  • 学习Spring必学的Java基础知识(5)—注解 bijian1013 javaspring
            文章来源：http://www.iteye.com/topic/1123823，整理在我的博客有两个目的：一个是原文确实很不错，通俗易懂，督促自已将博主的这一系列关于Spring文章都学完；另一个原因是为免原文被博主删除，在此记录，方便以后查找阅读。           有必要对
  • 【Struts2一】Struts2 Hello World bit1129 Hello world
    Struts2 Hello World应用的基本步骤 创建Struts2的Hello World应用，包括如下几步： 1.配置web.xml 2.创建Action 3.创建struts.xml，配置Action 4.启动web server，通过浏览器访问   配置web.xml <?xml version="1.0" encoding="
  • 【Avro二】Avro RPC框架 bit1129 rpc
    1. Avro RPC简介 1.1. RPC RPC逻辑上分为二层，一是传输层，负责网络通信；二是协议层，将数据按照一定协议格式打包和解包 从序列化方式来看，Apache Thrift 和Google的Protocol Buffers和Avro应该是属于同一个级别的框架，都能跨语言，性能优秀，数据精简，但是Avro的动态模式（不用生成代码，而且性能很好）这个特点让人非常喜欢，比较适合R
  • lua　set get cookie ronin47 lua cookie
    lua: local access_token = ngx.var.cookie_SGAccessToken if access_token then ngx.header["Set-Cookie"] = "SGAccessToken="..access_token.."; path=/;Max-Age=3000" end
  • java-打印不大于N的质数 bylijinnan java
    public class PrimeNumber { /** * 寻找不大于N的质数 */ public static void main(String[] args) { int n=100; PrimeNumber pn=new PrimeNumber(); pn.printPrimeNumber(n); System.out.print
  • Spring源码学习-PropertyPlaceholderHelper bylijinnan javaspring
    今天在看Spring 3.0.0.RELEASE的源码，发现PropertyPlaceholderHelper的一个bug 当时觉得奇怪，上网一搜，果然是个bug，不过早就有人发现了，且已经修复： 详见： http://forum.spring.io/forum/spring-projects/container/88107-propertyplaceholderhelper-bug
  • [逻辑与拓扑]布尔逻辑与拓扑结构的结合会产生什么? comsci 拓扑
       如果我们已经在一个工作流的节点中嵌入了可以进行逻辑推理的代码,那么成百上千个这样的节点如果组成一个拓扑网络,而这个网络是可以自动遍历的,非线性的拓扑计算模型和节点内部的布尔逻辑处理的结合,会产生什么样的结果呢?    是否可以形成一种新的模糊语言识别和处理模型呢?  大家有兴趣可以试试,用软件搞这些有个好处,就是花钱比较少,就算不成
  • ITEYE 都换百度推广了 cuisuqiang GoogleAdSense百度推广广告外快
    以前ITEYE的广告都是谷歌的Google AdSense，现在都换成百度推广了。   为什么个人博客设置里面还是Google AdSense呢？   都知道Google AdSense不好申请，这在ITEYE上也不是讨论了一两天了，强烈建议ITEYE换掉Google AdSense。至少，用一个好申请的吧。   什么时候能从ITEYE上来点外快，哪怕少点
  • 新浪微博技术架构分析 dalan_123 新浪微博架构
    新浪微博在短短一年时间内从零发展到五千万用户，我们的基层架构也发展了几个版本。第一版就是是非常快的，我们可以非常快的实现我们的模块。我们看一下技术特点，微博这个产品从架构上来分析，它需要解决的是发表和订阅的问题。我们第一版采用的是推的消息模式，假如说我们一个明星用户他有10万个粉丝，那就是说用户发表一条微博的时候，我们把这个微博消息攒成10万份，这样就是很简单了，第一版的架构实际上就是这两行字。第
  • 玩转ARP攻击 dcj3sjt126com r
    我写这片文章只是想让你明白深刻理解某一协议的好处。高手免看。如果有人利用这片文章所做的一切事情，盖不负责。 网上关于ARP的资料已经很多了，就不用我都说了。 用某一位高手的话来说，“我们能做的事情很多，唯一受限制的是我们的创造力和想象力”。 ARP也是如此。 以下讨论的机子有 一个要攻击的机子：10.5.4.178 硬件地址：52:54:4C:98
  • PHP编码规范 dcj3sjt126com 编码规范
    一、文件格式 1. 对于只含有 php 代码的文件，我们将在文件结尾处忽略掉 "?>" 。这是为了防止多余的空格或者其它字符影响到代码。例如：<?php$foo = 'foo';2. 缩进应该能够反映出代码的逻辑结果，尽量使用四个空格，禁止使用制表符TAB，因为这样能够保证有跨客户端编程器软件的灵活性。例
  • linux 脱机管理（nohup） eksliang linux nohupnohup
    脱机管理 nohup 转载请出自出处：http://eksliang.iteye.com/blog/2166699 nohup可以让你在脱机或者注销系统后，还能够让工作继续进行。他的语法如下 nohup [命令与参数] --在终端机前台工作 nohup [命令与参数] & --在终端机后台工作   但是这个命令需要注意的是，nohup并不支持bash的内置命令，所
  • BusinessObjects Enterprise Java SDK greemranqq javaBOSAPCrystal Reports
    最近项目用到oracle_ADF  从SAP/BO 上调用 水晶报表，资料比较少，我做一个简单的分享，给和我一样的新手 提供更多的便利。   首先，我是尝试用JAVA JSP 去访问的。   官方API：http://devlibrary.businessobjects.com/BusinessObjectsxi/en/en/BOE_SDK/boesdk_ja
  • 系统负载剧变下的管控策略 iamzhongyong 高并发
    假如目前的系统有100台机器，能够支撑每天1亿的点击量（这个就简单比喻一下），然后系统流量剧变了要，我如何应对，系统有那些策略可以处理，这里总结了一下之前的一些做法。 1、水平扩展 这个最容易理解，加机器，这样的话对于系统刚刚开始的伸缩性设计要求比较高，能够非常灵活的添加机器，来应对流量的变化。 2、系统分组 假如系统服务的业务不同，有优先级高的，有优先级低的，那就让不同的业务调用提前分组
  • BitTorrent DHT 协议中文翻译 justjavac bit
    前言 做了一个磁力链接和BT种子的搜索引擎 {Magnet & Torrent}，因此把 DHT 协议重新看了一遍。 BEP: 5Title: DHT ProtocolVersion: 3dec52cb3ae103ce22358e3894b31cad47a6f22bLast-Modified: Tue Apr 2 16:51:45 2013 -070
  • Ubuntu下Java环境的搭建 macroli java工作ubuntu
    配置命令： 　　$sudo apt-get install ubuntu-restricted-extras 　　再运行如下命令： 　　$sudo apt-get install sun-java6-jdk 　　待安装完毕后选择默认Java. 　　$sudo update- alternatives --config java 　　安装过程提示选择，输入“2”即可，然后按回车键确定。
  • js字符串转日期（兼容IE所有版本） qiaolevip TODateStringIE
    /** * 字符串转时间（yyyy-MM-dd HH:mm:ss） * result （分钟） */ stringToDate : function(fDate){ var fullDate = fDate.split(" ")[0].split("-"); var fullTime = fDate.split("
  • 【数据挖掘学习】关联规则算法Apriori的学习与SQL简单实现购物篮分析 superlxw1234 sql数据挖掘关联规则
    关联规则挖掘用于寻找给定数据集中项之间的有趣的关联或相关关系。 关联规则揭示了数据项间的未知的依赖关系，根据所挖掘的关联关系，可以从一个数据对象的信息来推断另一个数据对象的信息。 例如购物篮分析。牛奶 ⇒ 面包 [支持度：3%，置信度：40%] 支持度3%：意味3%顾客同时购买牛奶和面包。 置信度40%：意味购买牛奶的顾客40%也购买面包。 规则的支持度和置信度是两个规则兴
  • Spring 5.0 的系统需求，期待你的反馈 wiselyman spring
                   Spring 5.0将在2016年发布。Spring5.0将支持JDK 9。          Spring 5.0的特性计划还在工作中，请保持关注，所以作者希望从使用者得到关于Spring 5.0系统需求方面的反馈。  
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他