图元处理(Primitive Processing)
- 如何在场景中使用曲面细分来添加几何细节
- 如何使用几何着色器处理整个图元并且立即创建新的几何体
对于每一个发送到OpenGL的顶点,顶点着色器都会运行一次并输出一个数据集合。接来来的几个阶段和顶点着色器有一定的相似之处,实际上它们被称为图元处理阶段。首先,曲面细分着色器处理图形块(patches),接下来几何着色器处理整个图元(点、线、面),对于每个图元它都会运行一次。
1 曲面细分(Tessellation)
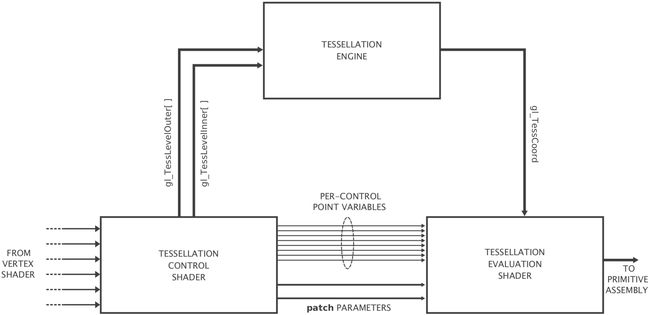
曲面细分指的是将被称为图像块(patch)的几何体在其被渲染之前分割成更小的图元。曲面细分的应用场景很多,最常见的是用于为低保真度的网格添加几何细节。在OpenGL中,曲面细分过程分为3个阶段:曲面细分控制着色器(TCS),固定曲面细分引擎,曲面细分评价着色器(TES)。当曲面细分引擎被激活时,顶点着色器如一般状态下一样一次处理顶点数据,然后将数据分组发送给曲面细分控制着色器。
曲面细分控制着色器操作的单个数据组最多支持至少32个顶点(具体个数使参数GL_ MAX_ PATCH_ VERTICES查询),他们合起来被称为一个图形块(patch)。其曲面细分大阶段内,输入顶点通常被称为控制点(control points)。曲面细分控制着色器有下述3个职责。
- 确定每个图形块的内部和外部曲面细分因子
- 确定每个输出控制点的位置和其他属性
- 确定每个图形块的用户定义渐变量
曲面细分因子被发送至曲面细分引擎,用于确定OpenGL细分图元的方式。在曲面细分引擎运行后,曲面细分控制着色器确定的控制点集合将会被发送给曲面细分求值着色器。一些变量如果对于所有的输出顶点都是相同的(例如图形块的颜色),它们将被标记为按图形块计算(be marked as per patch)。当曲面细分大阶段运行后,它会生成一个新的顶点集合,它们按照曲面细分因子和曲面细分模式定义的方式分布于图形块中,曲面细分模式可以通过在曲面求值着色器中以布局声明的方式定义。曲面细分求值着色器中的唯一输入变量几何为OpenGL生成的坐标集合,它们保存了新的顶点在图形块中的位置信息。当生成的图元类型是三角形时,这些坐标为重力坐标。当曲面细分引擎生成线或者三角形时,这些坐标仅仅是标准化的值,表示顶点的相对位置,它们被保存在变量gl_TessCoord中。该机制概括如下图。
1.1 曲面细分图元模式(Tessellation Primitive Modes)
曲面细分模式决定了OpenGL如何将图形块分解为图元。该模式通过在曲面细分计算着色器中使用声明关键字quads、triangles或者isolines设置。图元模式不仅决定了曲面细分阶段生成的图元类型,同时还影响了再曲面细分计算着色器中关键字gl_TessCoord的含义。
1.1.1 Quads模式
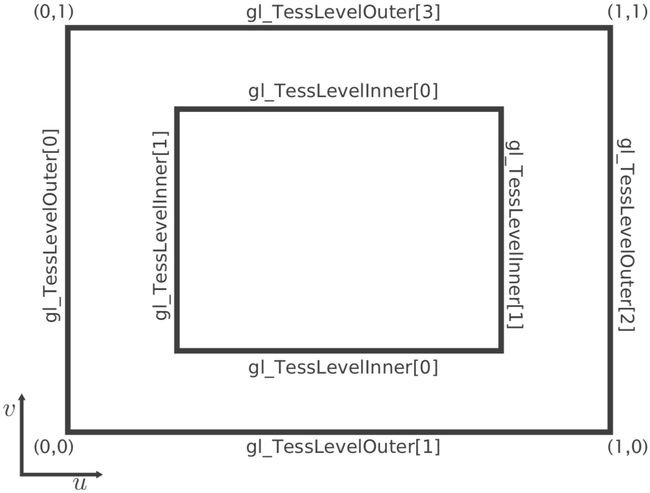
在使用Quads模式进行曲面细分时,曲面细分引擎会生成一个四边形,并将其分解为三角形集合。曲面细分控制着色器需要设置一个包含两个元素的gl_TessLevelInner[]数组,它控制了四边形内部的曲面细分等级。数组中第一个元素据定了水平方向上的细分等级,而第二个元素决定了垂直方向上细分等级。同样的,曲面细分控制着色器还需要设置一个包含4个元素的gl_TessLevelOuter[]数组,它们分别控制外边的细分等级。细分规律示意如下。
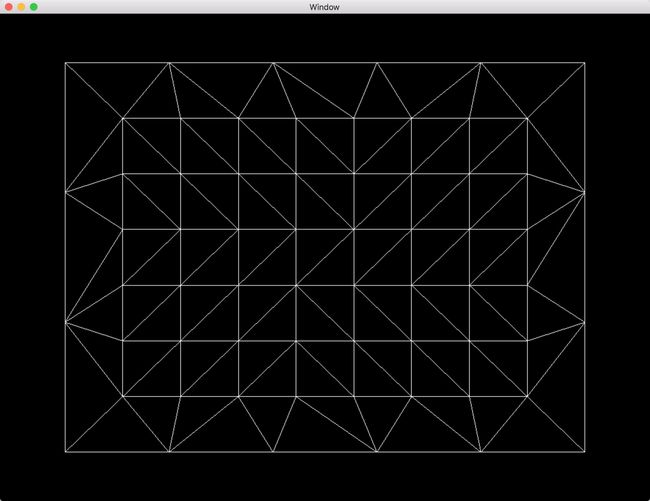
当四边形被曲面细分后,曲面细分引擎会在四边形标准化后的两维空间内生成一系列的顶点。每个顶点的标注化二维坐标以二维向量(也就是说只有其x和y分量是有效的)的方式保存在变量gl_TessCorrd内,该变量会被传递到曲面细分计算着色器内,结合由曲面细分控制着色器确定的控制点坐标就能计算出顶点坐标。一个该模式曲面细分实例如下,在图中可以看见在外部边缘横轴和竖轴方向分别被平分为5和3份,内部同样的分别被平分为9和7份。源代码请见Chapter 8/8.9-tessmodes。
在上述实例中,内部的细分因子分别被设置为9和7,外部的细分因子分别被设置为3和5。曲面细分控制着色器核心代码如下。
#version 410 core
layout (vertices = 4) out;
void main() {
if (gl_InvocationID == 0) {
gl_TessLevelInner[0] = 9.0;
gl_TessLevelInner[1] = 7.0;
gl_TessLevelOuter[0] = 3.0;
gl_TessLevelOuter[1] = 5.0;
gl_TessLevelOuter[2] = 3.0;
gl_TessLevelOuter[3] = 5.0;
}
gl_out[gl_InvocationID].gl_Position = gl_in[gl_InvocationID].gl_Position;
}
核心的曲面细分计算着色器代码如下,注意其中曲面细分模式的声明方式。
#version 410 core
layout (quads) in;
void main() {
// 此处直接提供在quads细分模式下顶点坐标计算,并不推导公式
// Interpolate along bottom edge using x component of the tessellation coordinate
vec4 p1 = mix(gl_in[0].gl_Position, gl_in[1].gl_Position, gl_TessCoord.x);
// Interpolate along top edge using x component of the tessellation coordinate
vec4 p2 = mix(gl_in[2].gl_Position, gl_in[3].gl_Position, gl_TessCoord.x);
// Now interpolate those two results using the y component of tessellation coordinate
gl_Position = mix(p1, p2, gl_TessCoord.y);
}
1.1.2 Triangles模式
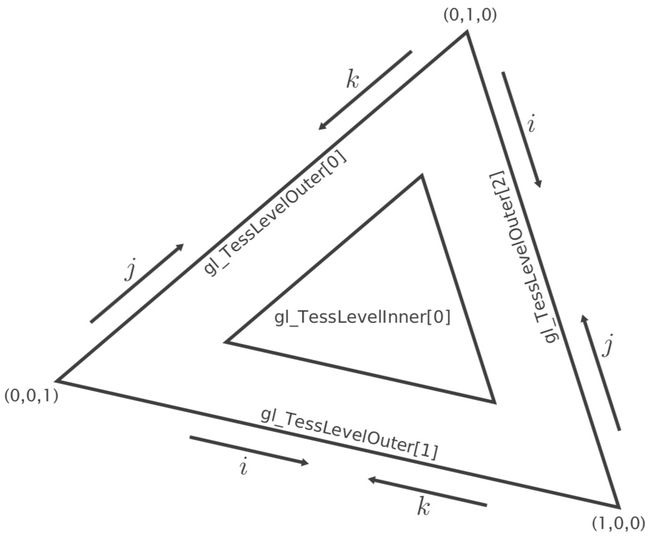
当曲面细分魔法被设置为三角形时,曲面细分引擎首先生成一个三角形,再将其分解为更小的三角形。曲面细分控制着色器中需设置一个包含1个元素的数组gl_TessLevelInner[],它决定了内部三角形的细分等级。包含3个元素的数组gl_TessLevelOuter[]分别决定了三条边的细分等级,其细分规律可用下图表示。
曲面细分引擎将为每个顶点生成3维重心坐标,结合三角形的三个顶点坐标可以在三角形内部进行线性插值计算出所有点的坐标。三角形细分模式的实例如下,可以看见图中外边都被分为8等份,内边被等分为5等份。源代码请见Chapter 8/8.9-tessmodes。
其曲面细分控制着色器代码如下。
#version 410 core
layout (vertices = 3) out;
void main() {
if (gl_InvocationID == 0) {
gl_TessLevelInner[0] = 5.0;
gl_TessLevelOuter[0] = 8.0;
gl_TessLevelOuter[1] = 8.0;
gl_TessLevelOuter[2] = 8.0;
}
gl_out[gl_InvocationID].gl_Position = gl_in[gl_InvocationID].gl_Position;
}
其曲面细分计算着色器源代码如下。
#version 410 core
layout (triangles) in;
void main() {
gl_Position = (gl_TessCoord.x * gl_in[0].gl_Position) + (gl_TessCoord.y * gl_in[1].gl_Position) + (gl_TessCoord.z * gl_in[2].gl_Position);
}
1.1.3 Isolines模式
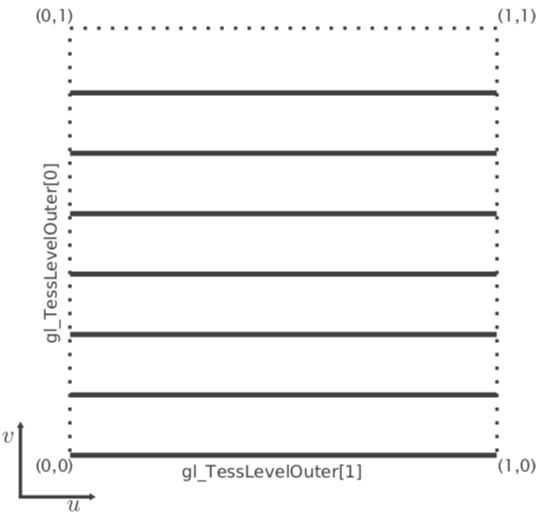
曲面细分模式设置为Isoline模式时,曲面细分引擎不再生成三角形,而是沿着y轴生成等y值的水平线图元,同时每条线沿着水平方向再被分解为多个等长片段。数组gl_TessLevelOuter[]中的两个元素分别表示了线的条数和每条线上的片段数,此时数组gl_TessLevelInner[]中的元素没有任何意义。其分解原理如下所示。
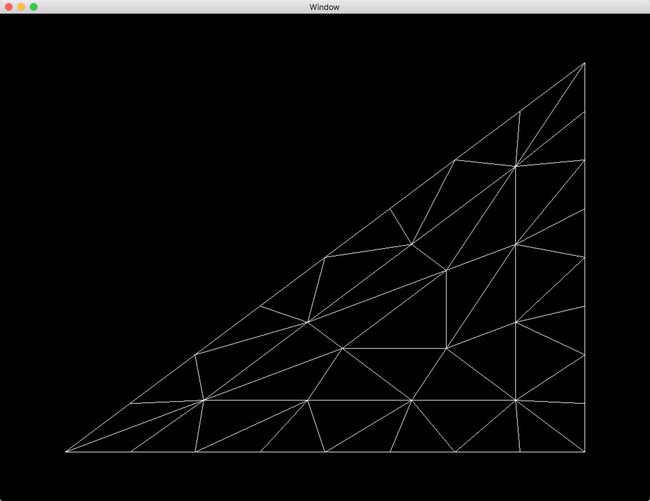
使用Isolines细分的实例如下,注意尽管下图中每条线段看上去是一个整体,但是实际上它们都是由5个小线段组成,源代码请见Chapter 8/8.9-tessmodes。
其曲面细分控制着色器代码如下。
#version 410 core
layout (vertices = 4) out;
void main() {
if (gl_InvocationID == 0) {
gl_TessLevelOuter[0] = 5.0;
gl_TessLevelOuter[1] = 5.0;
}
gl_out[gl_InvocationID].gl_Position = gl_in[gl_InvocationID].gl_Position;
}
其曲面细分计算着色器代码如下。
#version 410 core
layout (isolines) in;
void main() {
// Interpolate along bottom edge using x component of the tessellation coordinate
vec4 p1 = mix(gl_in[0].gl_Position, gl_in[1].gl_Position, gl_TessCoord.x);
// Interpolate along top edge using x component of the tessellation coordinate
vec4 p2 = mix(gl_in[2].gl_Position, gl_in[3].gl_Position, gl_TessCoord.x);
// Now interplate those two results using the y component of tessellation coordinate
gl_Position = mix(p1, p2, gl_TessCoord.y);
}
为了更好的区分其中的每个线段,采用如下曲面细分计算着色器代码对线的控制点镜像旋转处理,得到以下结果。
其对应的曲面细分计算着色器代码如下。
void main() {
float r = (gl_TessCoord.y + gl_TessCoord.x / gl_TessLevelOuter[0]);
float t = gl_TessCoord.x * 2.0 * 3.14159;
gl_Position = vec4(sin(t)*r, cos(t)*r, 0.5, 1.0);
}
1.1.4 点模式
使用关键字layout声明point_mode可以启用点细分模式,此时曲面细分模块会生成点图元。该模式是对quads、triangles或者isolines模式的进一步定义,因此在使用点模式时还需要指定上述3个模式中的一个,它们控制了图元内部和外部的线性插值。具体的细分因子和细分点坐标和quads、triangles或者isolines模式中描述的一致。
1.2 曲面细分模式(Tessellation Subdivision Modes)
曲面细分引擎工作的方式是生成一个四边形或者三角形图元,然后再根据控制着色器中定义的内部和外部细分因子将其内外边分为多个片段。再将生成的顶点按照点、线和三角形分组以备进一步处理。在该过程中OpenGL提供了一些关键字用于控制细分图元边的方式。
默认情况下,曲面细分引擎会将每条边分为相等的多个部分。默认的关键字为equal_spacing,尽管它是默认模式,仍能在曲面细分计算着色器中通过如下方式声明。layout (equal_spacing) in。
等分模式是最简单的,它总会咦寻找到等于或者大于设置值的一个最近的整数,但是该方式也有缺陷,在两个相邻的细分等级直接图形的表现不会存在过度,而是突变的。为了处理这个问题,OpenGL还提供了另外两个模式fractional_even_spacing和fractional_odd_spacing。
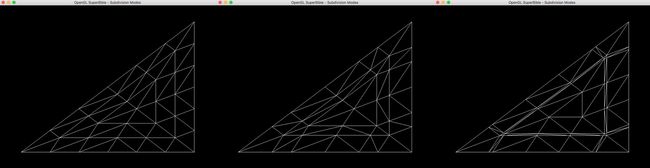
在这两种模式下,曲面细分着色器会分别寻找当前设置细分因子SetFactor下最接近的偶数RealFactorEven和奇数RealFactorOdd,在此基础上将剩余部分FactorRemain分为两等份FractionFactor。两种模式分别以RealFactorEven+2 FractionFactor和FactorRemain +2FractionFactor的模式细分对应的边。三种不同的细分模式示意图如下。从左到右依次为equal_spacing 、fractional_even_spacing和fractional_odd_spacing。
可以通过使用uniform变量或者直接在着色器内部均匀的对曲面细分等级做出变化,从而使得对应的细分线段长度也跟着动态的均匀变化。奇数模式和偶数模式的选择取决于它们在程序中的表现,并没有绝对的最优选择。但是除非特殊需求,采用渐变模式的视觉效果都会比突变模式更好。
1.2.1 控制旋转顺序
通常,图元的生成的旋转模式取决于程序提供给OpenGL的顶点组成顺序。但是,当曲面细分被激活后,为了控制生成图元生成时的旋转顺序,需要手动指定顶点的生成顺序为顺时针或者逆时针。在曲面细分计算引擎中分别通过如下关键字生成指定顺时针和逆时针模式layout (cw) in;和layout (ccw) in;。
默认模式下,OpenGL采用的是逆时针模式,如果该模式是希望的图元生成旋转顺序,那么可以不再在着色器中声明。另外,该定义只对三角形的图元模式有效,如果是线或者点模式,该声明无任何意义,将会直接被OpenGL忽略。
1.3 曲面细分着色器中的数据传递(Passing Data between Tessellation Shaders)
在曲面细分控制着色器运行之前,每个顶点代表了一个控制点,都会独立运行一次顶点着色器生成新的输出顶点。生成的顶点将会被分组传递到曲面细分控制着色器中。曲面细分控制着色器会处理这些控制点组,并生成新的控制点组,需要注意的是改着色器可以输入和输出的控制点组成员个数可以不同。尽管在该着色器中看上去能够获取到所有的控制点,但是它的运行次数和输出控制点个数相同。输入的控制点数组成员个数有以下函数在应用中设置。glPatchParameteri(GL_PATCH_VERTICES, n)。
输入顶点数据被包装在内嵌变量gl_in[]数组中,该数组中的每一个元素都是gl_PerVertex类型结构体,可以从中获取到位置信息,这些顶点数据都由顶点着色器设置。另外,顶点着色器中的所有输出都会被包装为数组传递到曲面细分控制着色器中。如在顶点着色器中声明了结构体,那么在曲面细分着色器中的声明必须为结构体数组。
out VS_OUT {
vec4 foo;
} vs_out;
顶点着色器总的上述声明转换到曲面细分控制着色器中声明方式如下
in VS_OUT {
vec4 foo;
} tcs_in[];
曲面细分着色器的输出同样也是一个数组,其数组成员个数由其着色器代码中的布局设置定义。通常的做法是直接将输入顶点数据不做修改直接传递到下一个着色器。但是需要注意的是,该着色器中的最大输出数组成员个数是有限的,可以通过常量GL_MAX_PATCH_VERTICES查询。
同样的,曲面细分计算着色器的输入也同样是一个数组,每计算一个顶点数据,它都会运行一次,但是每次运算它都能获取到所有的数据。
除了以数组的方式传递数据外,对于在整批数据中的常量,它们可以直接在曲面细分控制-计算着色器之间传递,只需要在两个着色器中对应的变量声明部分加上关键字patch。
1.3.1 不使用曲面细分控制器渲染
有时,应用中不为曲面细分计算着色器提供顶点数据,只需设置细分因子,此时在程序中可以只使用曲面细分计算着色器,而不使用曲面细分计算着色器。
当程序中没有曲面细分控制着色器时,默认的细分因子都为1,可以通过一下函数来为其赋值void glPatchParameterfv (GLenum pname, const GLfloat * values);。
其中参数可选GL _PATCH _DEFAULT _INNER _LEVEL和GL _PATCH _DEFAULT _OUTER _LEVEL,其值为包含曲面细分因子的数组。如果曲面细分控制着色器缺失,那么曲面细分计算着色器中的成员个数和每批处理的顶点个数相同。并且此时该着色器中的顶点数据直接来源于顶点着色器。
1.4 着色器调用之间的通信(Communication between Shader Invocations)
曲面细分控制着色器的作用不仅限于为下一个控制器提供必要的参数和数据,它还在多次控制着色器调用之间传递数据。因为当每个控制点被计算式它都会被调用一次,同时每次调用它都能获取到前一次调用时的输出数据。但是该类调用被设计为并发调用,因此无法确定在某一次调用时数组中的某个元素是否被计算完成。
为了处理这个问题,GLSL提供barrier()函数,它被称为流控制屏障,它能强制使得多个着色器调用以一定的顺序被执行。barrier()函数在后续文章中讲到计算着色器时再展开论述。在曲面细分控制着色器中它的使用会受到一定的限制,特别是该函数只能在main函数中直接调用,不能放入任何流控制结构中(如if、else、while或者Switch)。
在曲面细分控制着色器中调用函数barrier()后,当同批处理的顶点所运行的着色器都运行到该行代码时着色器才会继续运行,因此,如果在该行代码前输出了一个数组,那么之后的调用都能获取到该数组的完整数据。
1.5 曲面细分实例-地形渲染(Tessellation Example - Terrain Rendering)
为说明曲面细分的潜力,引用一个基于四边形模式的批顶点处理和位移贴图的实例。该示例的部分代码负责位移映射逻辑。位移贴图未一张包含有每个位置顶点和平面之间的位移值的纹理。每一批顶点都表示地形的一部分区域,它们根据其屏幕空间内来决定其曲面细分逻辑。每个曲面细分后的顶点都沿着它们到平面的切线移动一定的距离,位移值从位移贴图中获取。这样可以不用存储每一个曲面细分后顶点的位置信息就可以为平面添加更多的几何细节。需要注意的是,只有平面生成的位移才会被存储到位移贴图中,并且只有它们能够在运行时被用于曲面细分计算着色器。在示例中使用的位移贴图(也称为高度贴图)如下。
首先设置一个简单的顶点着色器,每一批顶点实际上都代表在xz平面上的一个简单四边形,可以在着色器中直接使用常量来表示顶点的坐标,不用通过顶点数组输入。完整的着色器如下。着色器中使用内置变量gl_InstanceID来计算每个批次顶点的偏移量,每个顶点原始的宽高都为1,中心位于原点。在下面的实例中将会渲染64乘64个图形块形成一个网格,因此计算每个图形块的x和y索引可以通过逻辑并和位移操作完成。同时顶点着色器还会计算每批顶点的纹理坐标,它将会被传递给曲面控制着色器。
#version 410 core
out VS_OUT {
vec2 tc;
} vs_out;
void main() {
const vec4 vertices[] = vec4[](vec4(-0.5, 0.0, -0.5, 1.0), vec4( 0.5, 0.0, -0.5, 1.0), vec4(-0.5, 0.0, 0.5, 1.0), vec4( 0.5, 0.0, 0.5, 1.0));
int x = gl_InstanceID & 63;
int y = gl_InstanceID >> 6;
vec2 offs = vec2(x, y);
vs_out.tc = (vertices[gl_VertexID].xz + offs + vec2(0.5)) / 64.0;
gl_Position = vertices[gl_VertexID] + vec4(float(x - 32), 0.0, float(y - 32), 0.0);
}
完整的曲面细分控制着色器代码如下。本实例中,大部分渲染逻辑都实现在曲面细分控制着色器中,不清绝大部分只有在首次调用时才会执行。通过内部变量gl_InvocationID等于0判断首次调用,计算细分因子。通过将输入坐标和模型视图投影矩阵相乘,并将其除以自生的w分量可以将每个图形块儿的四个控制点投影在标准设备坐标系内(顶点渲染这部分相关逻辑OpenGL会自动处理,这里手动计算是为了计算细分因子)(另外需要注意的是当矩形块被投影到标准设备坐标系后,可以将其看做为一个变形的平面图形,通常此时仅相对于屏幕的xy坐标分量有意义)。
接下来,计算出在标准设备坐标系中每个矩形块投影在xy平面上后其对应的各个边长。着色器对每个边长乘以1个缩放系数再加上一个基础值得到每个边上的曲面细分因子。并取水平和垂直方向上的最小值设置为内部曲面细分因子。
#version 410 core
layout (vertices = 4) out;
in VS_OUT {
vec2 tc;
} tcs_in[];
out TCS_OUT {
vec2 tc;
} tcs_out[];
uniform mat4 mvp;
void main() {
if (gl_InvocationID == 0) {
vec4 p0 = mvp * gl_in[0].gl_Position; vec4 p1 = mvp * gl_in[1].gl_Position;
vec4 p2 = mvp * gl_in[2].gl_Position; vec4 p3 = mvp * gl_in[3].gl_Position;
p0 /= p0.w; p1 /= p1.w; p2 /= p2.w; p3 /= p3.w;
// 此处模型坐标已经被转化为标准设备坐标NDC,而标准设备坐标系的z轴范围为1到-1,其中z轴正方向指向屏幕内部
// 这里剔除了位于观察者后面的图形块,优化着色器性能。
// 这种优化仍有瑕疵,当观察这位于十分陡峭的悬崖底部向上看时,单个patch会被拉伸,导致其部分位于观察者后,部分位于观察者视野内
if (p0.z <= 0.0 || p1.z <= 0.0 || p2.z <= 0.0 || p3.z <= 0.0) {
gl_TessLevelOuter[0] = 0.0; gl_TessLevelOuter[1] = 0.0;
gl_TessLevelOuter[2] = 0.0; gl_TessLevelOuter[3] = 0.0;
} else {
float l0 = length(p2.xy - p0.xy) * 16.0 + 1.0; float l1 = length(p3.xy - p2.xy) * 16.0 + 1.0;
float l2 = length(p3.xy - p1.xy) * 16.0 + 1.0; float l3 = length(p1.xy - p0.xy) * 16.0 + 1.0;
gl_TessLevelOuter[0] = l0; gl_TessLevelOuter[1] = l1;
gl_TessLevelOuter[2] = l2; gl_TessLevelOuter[3] = l3;
gl_TessLevelInner[0] = min(l1, l3); gl_TessLevelInner[1] = min(l0, l2);
}
}
gl_out[gl_InvocationID].gl_Position = gl_in[gl_InvocationID].gl_Position;
tcs_out[gl_InvocationID].tc = tcs_in[gl_InvocationID].tc;
}
当曲面细分控制着色器计算出细分因子后,并不对顶点做任何处理,直接将其传递给曲面细分计算着色器,其代码如下。首先计算出经过曲面细分后每个顶点的位置和纹理坐标,通过纹理坐标在对应的位移贴图中取出在y轴方向上的偏移值将其应用于各个顶点,再将生成的坐标左生MVP矩阵从而得到其在NDC上的最终位置。
#version 410 core
layout (quads, fractional_odd_spacing) in;
uniform sampler2D tex_displacement;
uniform mat4 mvp;
uniform float dmap_depth;
in TCS_OUT {
vec2 tc;
} tes_in[];
out TES_OUT {
vec2 tc;
} tes_out;
void main() {
vec2 tc1 = mix(tes_in[0].tc, tes_in[1].tc, gl_TessCoord.x);
vec2 tc2 = mix(tes_in[2].tc, tes_in[3].tc, gl_TessCoord.x);
vec2 tc = mix(tc2, tc1, gl_TessCoord.y);
vec4 p1 = mix(gl_in[0].gl_Position, gl_in[1].gl_Position, gl_TessCoord.x);
vec4 p2 = mix(gl_in[2].gl_Position, gl_in[3].gl_Position, gl_TessCoord.x);
vec4 p = mix(p2, p1, gl_TessCoord.y);
p.y += texture(tex_displacement, tc).r * dmap_depth;
gl_Position = mvp * p;
tes_out.tc = tc;
}
将计算出的纹理坐标传入片段着色器中,通过颜色纹理获取对应的颜色值。对应的片段着色器代码如下。
#version 410 core
out vec4 color;
layout (binding = 1) uniform sampler2D tex_color;
in TES_OUT {
vec2 tc;
} fs_in;
void main() {
color = texture(tex_color, fs_in.tc);
}
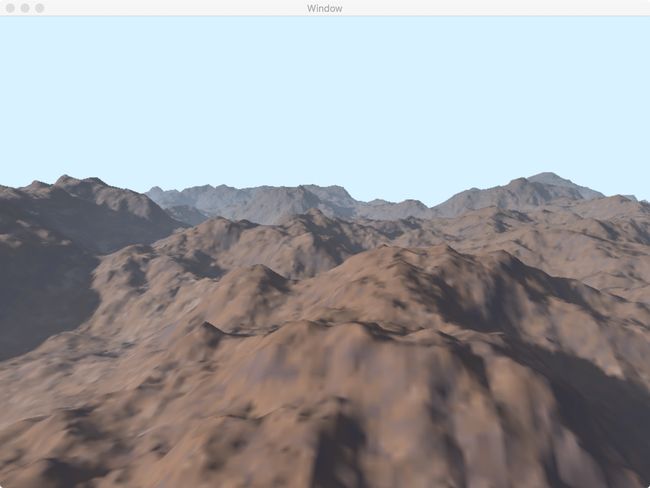
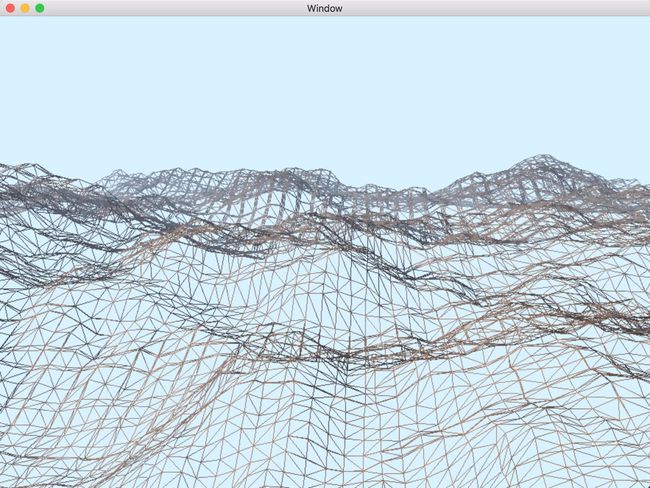
使用上述着色器渲染渲染的最终结果如下图所示,从表面上看并看不出底层的几何体已经被曲面细分。实例源代码见Chapter 8/8.11-dispmap。
然而当将由三角形构建的网格绘制出来后很明显的看出几何体经历曲面细分阶段,绘制的图像如下。该程序的目标是所有被渲染到屏幕上的三角形应该有基本相似的屏幕空间区域,并且细分因子的改变不应该引发剧烈的视觉差异。
1.6 曲面细分实例-立方体贝塞尔斑点(Cubic Bezier Patches)
在位移贴图的实例中,我们使用了一个非常大的纹理图来将平面拉升成地形图,同时使用曲面细分来提升场景中几何体的数量。这种靠着数据驱动实现复杂几何体的方式十分粗暴。在立方体贝塞尔实例中,将会通过渲染贝塞尔图形块儿的方式使用数学知识来实现复杂的几何体。贝塞尔曲线的相关知识在前面的章节OpenGL中的数学原理已经说明。
在本节示例中,只展示了单个贝塞尔图元的绘制,上个地形渲染转换成本实例的方式可以是将保存有多个贝塞尔图元的顶点数据的模型文件加载到程序中,通过instance多次绘制这些贝塞尔图形从而实现相同的地形渲染效果。
贝塞尔图形是一类高阶曲面,它由一些插值函数在一系列控制点中插值得到。贝塞尔图形有16个控制点,分布在4乘4的网格中。大多数情况下(包括本实例),这些控制点在二维平面上均匀分布,只在相对于一个共享平面的距离上发生改变。然而,它们并不是都服从这个规定。自由模式的贝塞尔图形是一个非常强大的模型处理工具,在很多建模和设计软件中都被大量使用。
一种简单渲染贝塞尔图形的方式是将其每行的4个控制点当成一个简单立方贝塞尔曲线的控制点对待。对于4乘4的网格,通过上述处理我们可以得到4条贝塞尔曲线。当t取某个值时,每个曲线分别得到一个固定的点,这样能得到多个由4个控制点组,由它们可以再得到一条新的贝塞尔曲线,这样便能得到贝塞尔曲面内部所有点的空间坐标。这里两次插值使用到的t分别对应gl_TessCoord中的x和y值。
本实例中,将在视图空间内执行曲面细分。这意味这需要先将图像块的控制点左乘model-view矩阵,从而将其坐标转换到视图空间内。顶点着色器代码如下。
#version 410 core
in vec4 position;
uniform mat4 mv_matrix;
void main(void) {
gl_Position = mv_matrix * position;
}
接下来将视图坐标系下的顶点传递给曲面细分控制着色器。在更高级的算法中,我们可以将控制点投影到屏幕空间上,根据曲线的长度来设置曲面细分因子(该算法必须估计贝塞尔曲线的长度,其中包含复杂的曲面积分)。在本示例中,仅仅设置一个固定的曲面细分因子。曲面细分控制着色器代码如下。
#version 410 core
layout (vertices = 16) out;
void main() {
if (gl_InvocationID == 0) {
gl_TessLevelInner[0] = 16.0;
gl_TessLevelInner[1] = 16.0;
gl_TessLevelOuter[0] = 16.0;
gl_TessLevelOuter[1] = 16.0;
gl_TessLevelOuter[2] = 16.0;
gl_TessLevelOuter[3] = 16.0;
}
gl_out[gl_InvocationID].gl_Position = gl_in[gl_InvocationID].gl_Position;
}
接下来将处理好的数据传入曲面细分计算着色器中。其中二次贝塞尔曲线和立方贝塞尔曲线的计算逻辑在前文中已经介绍过。图形计算函数根据输入的图形块控制点坐标和各个顶点在图形块内的位置计算出顶点的坐标,这是其被称为曲面细分计算着色器的原因。
#version 410 core
layout (quads, equal_spacing, cw) in;
uniform mat4 mv_matrix;
uniform mat4 proj_matrix;
out TES_OUT {
vec3 N;
} tes_out;
vec4 quadratic_bezier(vec4 A, vec4 B, vec4 C, float t) {
vec4 D = mix(A, B, t);
vec4 E = mix(B, C, t);
return mix(D, E, t);
}
vec4 cubic_bezier(vec4 A, vec4 B, vec4 C, vec4 D, float t) {
vec4 E = mix(A, B, t);
vec4 F = mix(B, C, t);
vec4 G = mix(C, D, t);
return quadratic_bezier(E, F, G, t);
}
vec4 evaluate_patch(vec2 at) {
vec4 P[4]; int I;
for (i = 0; i < 4; i++) {
P[i] = cubic_bezier(gl_in[i + 0].gl_Position,
gl_in[i + 4].gl_Position,
gl_in[i + 8].gl_Position,
gl_in[i + 12].gl_Position, at.y);
}
return cubic_bezier(P[0], P[1], P[2], P[3], at.x);
}
const float epsilon = 0.001;
void main(void) {
vec4 p1 = evaluate_patch(gl_TessCoord.xy);
vec4 p2 = evaluate_patch(gl_TessCoord.xy + vec2(0.0, epsilon));
vec4 p3 = evaluate_patch(gl_TessCoord.xy + vec2(epsilon, 0.0));
vec3 v1 = normalize(p2.xyz - p1.xyz);
vec3 v2 = normalize(p3.xyz - p1.xyz);
tes_out.N = cross(v1, v2);
gl_Position = proj_matrix * p1;
}
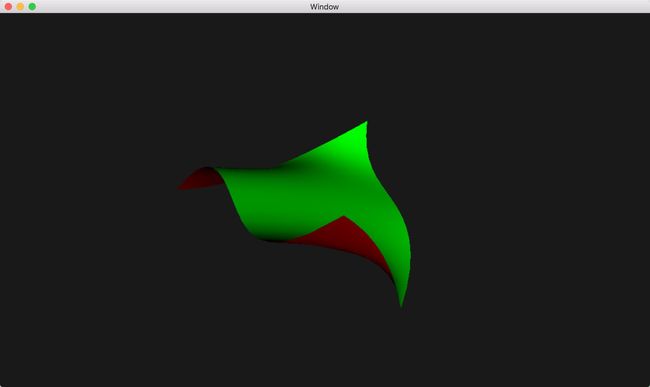
在曲面细分计算着色器内部,通过在顶点附近分别在x轴和y轴上进行一定偏移得到两个相邻点,从而进一步得到两个相邻,最后近似的计算出平面的法向量。并将法向量传入片段作色器内做计算片段的颜色值。最后使得变形前的图形从y轴上方看去为绿色,从y轴下方看去为红色。片段着色器代码如下。
#version 410 core
out vec4 color;
in TES_OUT {
vec3 N;
} fs_in;
void main(void) {
vec3 N = normalize(fs_in.N);
vec4 c = vec4(1.0, -1.0, 0.0, 0.0) * N.z + vec4(0.0, 0.0, 0.0, 1.0);
color = clamp(c, vec4(0.0), vec4(1.0));
}
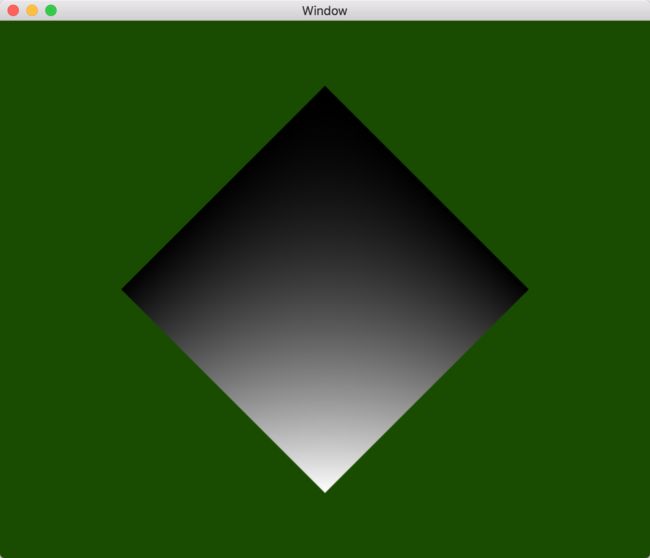
在片段着色器中,使用了平面法向量的z轴分量进行了简单的光照计算。渲染结果如下图。源代码见Chapter 8.14-cubicbezier。
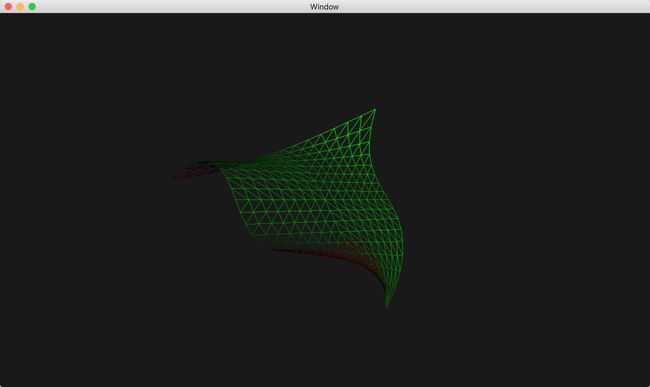
使用线绘制几何形能更清楚的看出图形块经历了曲面细分阶段,其绘制结果如下图。
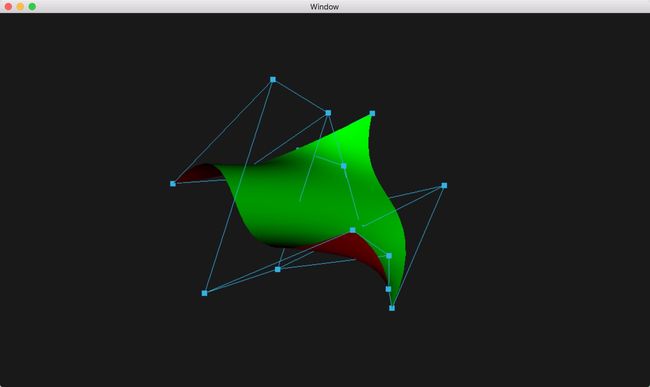
将控制点连线叠加在原图上绘制结果如下。
2 几何着色器(Geometry Shaders)
相较于其他类型的着色器,几何着色器有着独特的特性,它一次处理一个完整图元(点、线、面),并且能改变OpenGL渲染管道中的数据量。顶点着色器一次只能处理一个顶点,并且处理该顶点时不能获取其他顶点的信息,同时它是严格遵守单个顶点输入,单个顶点输出原则。曲面细分着色器操作图块(Patches),也可以设置曲面细分因子,但是对图块是怎样细分的控制能力并不强,也不能生成不连续的图元。相似的,片段着色器每次也仅能处理单个片段,不能获取其他片段的数据,不能新建片段,只能通过丢弃的方式销毁片段。另一方面,几何着色器可以获取到一个图元内(通过指定GL_TRIANGLES_ADJACENCY模式图元最多支持6分顶点)的所有顶点数据,能够改变图元的类型,甚至能创建和销毁图元。
在OpenGL渲染管道中,几何着色器是一个可选部分。当几何着色器不存在时,使用从顶点着色器或者曲面细分着色器输出的顶点数据在图元内部进行插值,然后依次将各个片段传递给片段着色器,最后实现图元的渲染。然而当几何着色器存在的时候,从顶点着色器和曲面细分计算着色器的输出数据将被传递到几何着色器,几何着色器重组的图元将对变成我们将要插值的对象,最后在将插值后的各个片段传递给片段着色器。另外几何着色器在重组图元的时候,它还可以对每个创建的图元都应用一个变形矩阵。
2.1 直通式几何着色器(The Pass-Through Geometry Shader)
在前文的例子中讲到过直通式的几何着色器,即对输入的图元不做任何更改直接输出,其代码如下。
#version 410 core
layout (triangles) in;
layout (triangle_strip) out;
layout (max_vertices = 3) out;
void main () {
for (int i = 0; i < gl_in.length(); i++) {
gl_Position = gl_in[i].gl_Position;
EmitVertex();
}
EndPrimitive();
}
该着色器的前几行中指定了输入图元为triangles,输出图元为triangle_strip(更多的图元类型将会在后面介绍)。几何着色器不仅需要指定输出的图元类型,还需要通过修饰符max_vertices指定最大的输出顶点个数。该实例中的着色器生成的时三角形条带,因此指定最大个数为3。
几何着色器的主函数看上去很像顶点着色器或者说是片段着色器。顶点着色器的所有输出都被包装成一个结构体,而单个图元的多个顶点的输出则被包装称为结构体数组传递给几何着色器,可以通过变量gl_in获得。数组的大小由输入图元的类型决定,在该实例中,输入图元是三角形,因此数组的大小为3。
该实例中,在循环内部仅仅将输入拷贝到输出中。输出结构和顶点着色器几曲面细分计算着色器类似,直接复制给内建变量gl_Position。当赋值完单个顶点的所有属性后必须调用函数EmitVertex()。该函数通知几何着色器我们已经完成了对该顶点的所有赋值操作,需要存储该顶点,并准备设置下一个顶点。
最后,当循环执行完毕,调用了另一个几何着色器的专有函数EndPrimitive()。该函数通知几何着色器我们已经完成了对当前图元所有顶点的赋值操作,即将处理下一个图元。在本实例中,我们指定了输出的图元类型为三角形条带,因此吐过我们连续调用超过三次EmitVertex()函数,OpenGL将会将三角形添加到连续的三角形条带中。如果我们像生成分离的三角形或者多个不相连的三角形条带,我们需要在它们之间调用函数EndPrimitive()。另外当程序没有调用该函数时,OpenGL会自动在几何着色器的末尾调用该函数。此外,本实例中生成的是分离的三角形构成的条带。
2.2 在应用中使用几何着色器(Using Geometry in an Application)
同其他着色器的创建方法相同,使用函数glCreateShader和参数GL_GEOMETRY_SHADE R创建几何着色器。同样的,使用函数glShaderSource管理着色器的源代码,使用glCompileShader编译着色器,使用函数glAttachShader将着色器和程序关联。然后使用函数glLinkProgram链接着色器。此时,当使用绘制函数如glDrawArrays时,顶点着色器为每个顶点运行一次,几何着色器为每个图元运行一次,片段着色器为每个片段运行一次。几何着色器的定义的输入图元和真实的输入图元类型必须有相关性,需要注意的是当曲面细分着色器未被启用时,几何着色器的定义的输入图元类型必须和调用绘制函数时的指定图元相匹配。完整的对应表如下。
几何着色器输入类型 允许的输出类型
points GL_POINTS
lines GL_LINES,GL_LINE_LOOP,GL_LINE_STRIP
triangles GL_TRIANGLES,GL_TRIANGLE_FAN,GL_TRIANGLE_STRIP
lines_adjacency GL_LINES_ADJACENCY
triangles_adjacency GL_TRIANGLES_ADJACENCY
当曲面细分引擎被激活是,使用绘制命令只能使用参数GL_PATCHES,OPenGL会在曲面细分的过程中将图块转化为点、线或者三角形图元。在本实例中,输入图元的类型和曲面细分着色器生成的图元类型相匹配。几何着色器接收到了一个完整图元的所有顶点参数,其内建变量gl_in的定义如下。
这里定义的gl_perVertex并非结构体,而是着色器直接特殊的传递类型变量block
in gl_perVertex {
vec4 gl_Position;
float gl_PointSize;
float gl_ClipDistance[];
} gl_in[];
对于顶点着色器中普通类型输出变量,在几何着色器中都应该被定义为相应的数组类型变量。举例如下。
// 在顶点着色器中的声明
out vec4 color;
out VertexData {
vec4 color;
vec3 normal;
} vertex;
// 在几何着色器中对应的声明
in vec4 color[];
out VertexData {
vec4 color;
vec3 normal;
} vertex[];
如果编写几何着色器时确定其需要处理的图元类型,那么可以明确的指定数组的大小,这样能在编译时节省额外的错误检查时间。当没有明确指定数组大小时,OpenGL将会根据输入的图元类型推断数组的大小,其对应关心如下。
Input Primitive Type Size of Input Arrays
points 1
lines 2
triangles 3
lines_adjacency 4
triangles_adjacency 6
另外,几何着色器必须指定输出的图元类型,格式为layout (primitive_type) out;。还必须指定几何着色器一次能输出的最大顶点数,格式为layout (max_vertices = n) out;,需要主要的是n的设置必须使得程序能够正常运行的最小值,例如当你获取点类型图元,要输出line类型图元时,n值最小为2,因为形成线图元的最小值为2。当曲面细分过于细时,可能需要将n值设置非常大,这会耗费更多的性能。n值的上限至少是256,可以通过函数glGetIntegerv和参数GL_ MAC_ GEOMETRY_ OUTPUT_ VERTIVCES获得准确的上限值。另外可以在单个布局声明中通过逗号分隔符定义多个布局属性,格式如layout (triangle_strip, max_vertices = n) out;。
如果几何着色器的源码中未调用函数EmitVertex或者函数EndPrimitive,渲染管道的所有图元传递到几何着色器后都会被丢弃。需要注意的是如果实现了main函数,并且未调用EndPrimitive方法,OpenGL会默认在main函数末尾调用该方法。正如在顶点着色器内部的工作,此处设置几何着色器处理后的剪切空间坐标(clip-space coordinates)。如果想从几何着色器传递其他变量到片段着色器,可以声明为block类型(interface block)或者全局变量类型。无论什么时候只要调用函数EmitVertex,几何着色器都会立即将数据存储到输出变量中,并且用它们生成一个新的顶点。
函数EndPrimitive表面向图元末尾追加顶点的工作已经完成。如果输出图元的类型为triangle_strip,并且调用函数EmitVertex的次数超过三次,几何着色器将会在单个条带内产生多个三角形。同样的,如果输出图元类型为line_strip,并且调用函数EmitVertex超过两次,将会在单个条带内得到多条线段。在几何着色器内,函数EndPrimitive表示单个条带的结束,这意味着如果需要绘制单独的线段或者三角形,需要在每两个或者三个顶点之后调用函数EndPrimitive。
最后需要提一点,如果在你调用EndPrimitive函数之前,调用EmitVertex函数的次数不足以组成单个图元(如使用的输出图元类型是triangle_strip,但是在调用函数EndPrimitive之前只生成了两个顶点),那么几何着色器讲不会生成新的图元,并且将已经生成的顶点数据全部丢弃。
2.3 在几何着色器中扔掉几何体(Discarding Geometry in the Geometry Shader)
通过调用函数EmitVertex追加足够的顶点,再调用函数EndPrimitive即可以生成新的图元,当然也可以不调用上述函数从而实现对图元的丢弃。为了说明这一点,设计了示例程序隐面剔除(backface culling)。当然OpenGL在几何处理器后,在光栅化之前,会有图元剔除步骤,并且可以设置剔除背面或者正面,这里的实例只做演示功能,实际项目中基本不会采取该方式统一剔除模型的背面图元。
在main函数中,我们需要找到三角形的面法向量。只需要通过三角形所在平面的两个法向量叉乘即可获得,再该实例中,可以使用三角形的两条边。代码如下。
vec3 ab = gl_in[1].gl_Position.xyz - gl_in[0].gl_Position.xyz;
vec3 ac = gl_in[2].gl_Position.xyz - gl_in[0].gl_Position.xyz;
// 计算模型坐标系中的图元法向量
vec3 normal = normalize(cross(ab, ac));
当得到法向量后,既可以确定该图元是面向还是背离观察者。具体做法是将面的法向量转换到观察坐标空间中,在本实例中也就是世界坐标空间。当包含model-view矩阵通用变量时,只需将其和法向量相乘即可。准确的描述是使用左上3*3的子矩阵和法向量相乘。 当然,吐过你的模型-视图矩阵只包含平移、三轴等比例缩放(uniform scale,不含剪切)以及旋转,你可以直接使用它和法向量相乘。但是,在此之前我们需要将法向量转化为4维向量。接下来我们通过获取转换后的法向量和观察向量的点乘结果来确定图元是面向还是背离观察者。
如果点乘的结果为负,意味着图元背向观察者,应该被剔除,剔除图元正如前文描述一样,只需要简单的不处理输入数据,那么该图元就会被丢弃。如果结果为正,那么图元面向观察者,此时需要新建图元。代码如下。
// 如果图元法向量和设置的视线逆向量夹角大于90度,即认为图元法向量背离观察者,即剔除该图元
if (dot(normal, vt) > 0.0) {
for (int n = 0; n < 3; n++) {
gl_Position = mvpMatrix * gl_in[n].gl_Position;
color = vertex[n].color;
EmitVertex();
}
EndPrimitive();
}
在该实例中,尽管我们选定的输出图元类型为triangle strip,但是我们仍然对每个输入的三角形图元只生成一个三角形输出图元,因此得到的条带都只包含单个三角形。这里函数EndPrimitive可以省略,此处为了代码的完整性特意列出。该项目的输出结果如下。完整的源代码请见8.16-glculling。
上图的每个小图都表示不同的观察者位置,正如图中所示,模型的不同部分被几何着色器剔除。该实例的实用性并不重要,它只是为了说明几何着色器有基于应用定义的准则实现几何体裁剪的能力。
2.4 在几何着色器中修改几何体(Modifying Geometry in the Geometry Shader)
除了丢弃图元外,几何着色器还可以输出和输入图元形状不相同的图元。即使几何着色器不改变顶点的个数,相对于只有顶点着色器,他仍能使我们能做更多的事情。例如,如果输入图元是三角形条带或扇,则输出的三角形会共享顶点和边,如果使用顶点着色器移动一个顶点,那么共享该顶点的所有三角形都会发生改变。然而,使用几何着色器即可对其中的单个三角形进行修改。
如果几何着色器接受三角形图元输入(输入不能是条带或者扇状图元),并输出三角形条带图元。那么无论使用绘制命令时调用的函数时glDrawArrays()或者是glDrawElements(),绘制的图元是三角形、三角形条带或者三角形条带,进入几何着色器的一定是独立的三角形。除非几何着色器输出时在调用结束图元前输出的顶点数大于3哥,输出结果都是独立的未连接的三角形。
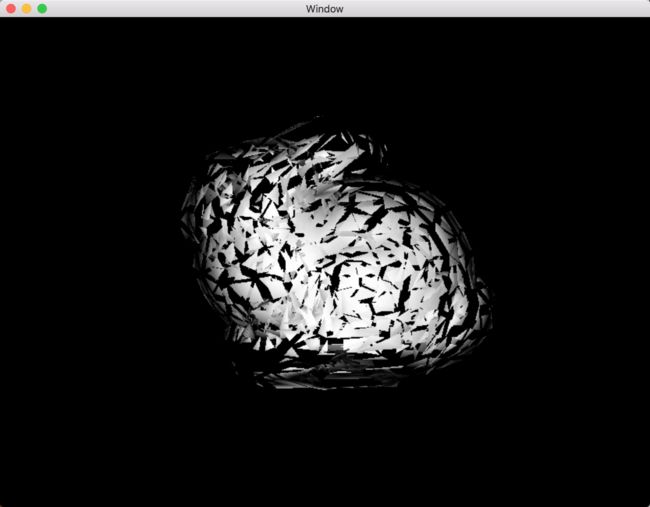
在下面的实例中,我们将“炸开一个模型”,使得它的三角形都沿着它们的面法向量向外移动。原始的模型是使用独立的三角形还是三角形条带或者是三角形扇绘制的并不重要。和上一个例子一样,几何着色器的输入是一个三角形,输出时一个三角形条带,几何着色器单个图元最大的顶点数为3,因为我们并未放大或者改变三角形。几何着色器的代码如下。
#version 410 core
layout (triangles) in;
layout (triangle_strip, max_vertices = 3) out;
in VS_OUT {
vec3 normal;
} gs_in[];
out GS_OUT {
vec3 normal;
} gs_out;
uniform float explode_factor = 0.1;
void main() {
vec3 ab = gl_in[1].gl_Position.xyz - gl_in[0].gl_Position.xyz;
vec3 ac = gl_in[2].gl_Position.xyz - gl_in[0].gl_Position.xyz;
// 这里三角形图元的法向量被乘以-1,是因为输入图元可能为顺时针
vec3 face_normal = -normalize(cross(ab, ac));
for (int i = 0; i < gl_in.length(); i++) {
// 在裁剪坐标系下,将兔子模型的图元沿着法向量进行平移,模拟爆炸效果
gl_Position = gl_in[i].gl_Position + vec4(face_normal * explode_factor, 0.0);
gs_out.normal = gs_in[i].normal;
EmitVertex();
}
EndPrimitive();
}
最后模拟的兔子炸裂效果如下图。Demo地址为8.17-gsexploder。
为了验证图元顶点输入顺时针和逆时针顺序对计算法向量的影响,特设计另外一个实验,其源码地址为8.17-0-normaloftriangle。左侧三角形的顶点输入顺序为顺时针,右侧为逆时针,同时沿着法向量移动一定的距离,可以看出左侧三角形向用户移动,二右侧三角形远离用户。在右手坐标系下,通常我们将面向用户的图元以逆时针输入顶点。
生成图元
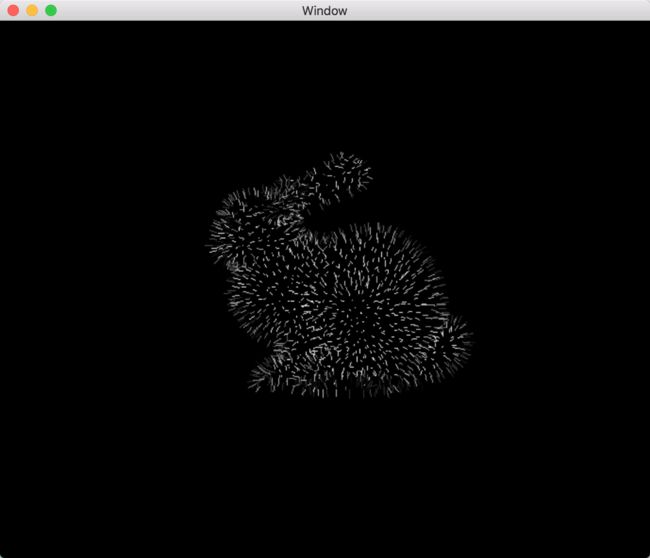
正如不调用函数EmitVertex和函数EndPrimitive可以丢弃图元,多次调用它们可以生成新的图元。这就是说,在调用调用函数EndPrimitive之前,如果调用函数EmitVertex次数达到在几何着色器头部声明的最大顶点数后。在几何着色器中可以拷贝多个输入图元,或者将输入图元分解为更小的碎片,这也是下面的实例演示的内容。输入的模型是一个绕原点的四面体,它每一面由一个三角形图元组成。沿着每条边的中点细分输入的三角形图元,然后移动所有生成的顶点,使它们到原点的距离都不相同。这样将四面体转换为钉状几何体。
在这里,由于几何着色器在物体空间操作(object space)(需要注意,四面体的中心点是原点),因此在顶点着色器中,不需要进行任何处理,而是在几何着色器中对新生成的顶点坐标进行投影变换。另外,顶点着色器中如果存在纹理坐标和法向量等属性,也应该直接传入几何着色器。
在几何着色器中,其输入图元为三角形,其输出图元为有单个三角形组成的条带。当三角形图元输入后,几何着色器会将其分解为4个三角形图元。我们需要声明最大的输出顶点数为12。
#version 410 core
layout (triangles) in;
layout (triangle_strip, max_vertices = 12) out;
uniform float stretch = 0.3;
// 这里意味这演示变量不会被线性插值,https://stackoverflow.com/questions/27581271/flat-qualifier-in-glsl
flat out vec4 color;
uniform mat4 mvMatrix;
uniform mat4 mvpMatrix;
void make_face(vec3 a, vec3 b, vec3 c) {
vec3 face_normal = normalize(cross(c - a, c - b));
vec4 face_color = vec4(1.0, 0.2, 0.4, 1.0) * (mat3(mvMatrix) * face_normal).z;
gl_Position = mvpMatrix * vec4(a, 1.0);
color = face_color;
EmitVertex();
gl_Position = mvpMatrix * vec4(b, 1.0);
color = face_color;
EmitVertex();
gl_Position = mvpMatrix * vec4(c, 1.0);
color = face_color;
EmitVertex();
EndPrimitive();
}
void main() {
int n;
vec3 a = gl_in[0].gl_Position.xyz;
vec3 b = gl_in[1].gl_Position.xyz;
vec3 c = gl_in[2].gl_Position.xyz;
// 此处计算三角形从一个顶点连向对边中点及其延长线上的向量,a+b为原点到ab边中点构成的向量*2
vec3 d = (a + b) * stretch;
vec3 e = (b + c) * stretch;
vec3 f = (c + a) * stretch;
// 放大器原始顶点,是钉状形状更加突出
a *= (2.0 - stretch);
b *= (2.0 - stretch);
c *= (2.0 - stretch);
// 此处将单个三角形图元分解为四个小的三角形图元
make_face(a, d, f);
make_face(d, b, e);
make_face(e, c, f);
make_face(d, e, f);
EndPrimitive();
}
使用几何着色器处理复杂的曲面细分可能不能得到最佳的性能。如果想要的曲面细分效果比本实例中的更复杂,最好使用曲面细分引擎来完成该需求。然而,如果只是为单个图元生成2~4个输出图元,可能使用几何着色器更方便。本实例的效果如下。Demo地址:8.18-gstessellate。
2.5 在几何着色器中改变图元类型(Changing the Primitive Type in the Geometry Shader)
到目前为止,所有的几何着色器例子并没有改变图元的类型。但是实际上,几何着色器可以改变图元类型,例如将点图元转换为三角形,或者将三角形转换为点图元。在下面的例子中,我们将三角形图元转换为线图元。我们会计算顶点法向量并以线图元的方式展示,也会计算面的法向量并展示成为另外一条线。这可以使我们通过顶点和图元的法向量去观察模型。需要注意的是,如果你想在模型的基础上观察法向量,那么你需要绘制两次。第一次不使用几何着色器渲染模型,第二次使用几何着色器可视化法向量。单个几何着色器不能同时输出两种图元。在本实例中的几何着色器中,除了gl_in内置变量,我们还需要每个顶点的法向量,该变量可以从顶点着色器中传入几何着色器。几何着色器的代码如下。
#version 410 core
layout (triangles) in;
layout (line_strip, max_vertices = 4) out;
uniform mat4 mv_matrix;
uniform mat4 proj_matrix;
in VS_OUT {
vec3 normal;
vec4 color;
} gs_in[];
out GS_OUT {
vec3 normal;
vec4 color;
} gs_out;
uniform float normal_length = 0.2;
void main() {
mat4 mvp = proj_matrix * mv_matrix;
vec3 ab = gl_in[1].gl_Position.xyz - gl_in[0].gl_Position.xyz;
vec3 ac = gl_in[2].gl_Position.xyz - gl_in[0].gl_Position.xyz;
vec3 face_normal = normalize(cross(ab, ac));
vec4 tri_centroid = (gl_in[0].gl_Position +
gl_in[1].gl_Position +
gl_in[2].gl_Position) / 3.0;
gl_Position = mvp * tri_centroid;
gs_out.normal = gs_in[0].normal;
gs_out.color = gs_in[0].color;
EmitVertex();
gl_Position = mvp * (tri_centroid +
vec4(face_normal * normal_length, 0.0));
gs_out.normal = gs_in[0].normal;
gs_out.color = gs_in[0].color;
EmitVertex();
EndPrimitive();
gl_Position = mvp * gl_in[0].gl_Position;
gs_out.normal = gs_in[0].normal;
gs_out.color = gs_in[0].color;
EmitVertex();
gl_Position = mvp * (gl_in[0].gl_Position +
vec4(gs_in[0].normal * normal_length, 0.0));
gs_out.normal = gs_in[0].normal;
gs_out.color = gs_in[0].color;
EmitVertex();
EndPrimitive();
}
在几何着色器中,输入类型图元为三角形,输出图元为由单个线段组成的线段条带。因为我们需要为每个可视化的法向量生成一条单独的线段,因此每消耗一个顶点,都会生成两个顶点表示点的法向量,两个顶点表示面法向量。因此每个三角形图元输出的最大顶点数为8。
每个输入的顶点被转换到它在世界坐标系中的位置,然后被输出几何着色器,然后通过该顶点的法向量向外截取标准长度用于生成第二个顶点,经过同样的转换后被输出几何着色器。这样我们的法向量长度都为1,但是最后呈现在屏幕上的模型仍能体现出模型-视图-投影矩阵的改变。将着色器提供的变量和法向量相乘,表示点法向量的线段长度和模型相匹配。
我们通过三角形图元的两个边相乘的到面法向量,选则三角形的重心为面法向量的起点,沿着面法向量截取单位长度并乘以着色器中定义的法向量长度从而获得第二个顶点,同样将它们转化到视图坐标系中。
该实例的最终渲染效果如下图所示。Demo地址为Chapter 8.19-normalviewer。
2.6 多重流存储(Multiple Streams of Storage)
当只有顶点着色器存在时,对于输入到着色器中的顶点以及存储在转换反馈缓存中的顶点之间是简单的单进单出关系。当几何着色器存在的时候,每个着色器调用可能会在转换反馈缓存(transform feedback buffers)中存储0个/1个或者更多的顶点。不仅如此,我们甚至能够配置4个输出流,同时使用几何着色器将输出发送到任意一个选中的输出流中。该策略可以用于分类几何体(sort geometry)或者在将几何体存入转换反馈缓存中的同时渲染部分图元。
在几何着色器中使用多重输出流仍有一些限制。首先,从几何着色器中输出的所有输出流的图元模式都必须是点图元(points)。其次,尽管可以在渲染模型的同时将顶点数据存入转换反馈缓存中,只有第一个流可以被渲染,剩余的输出流都只能作为存储使用。如果上述两个限制和产品需求不冲突,那么多重流将是一个强大的特性。
要在几何着色器中使用多重流特性,需要使用布局修饰词stream来设置变量应该输出到哪个流之中。stream关键字的用法如下所示。
out vec4 foo; //"foo" is in stream 0 (the default).
layout (stream=2) out vec4 bar; //"bar" is part of stream 2.
out vec4 baz; //"baz" is back in stream 0.
layout (stream=1) out; //Everything from here on is in stream 1.
out int apple; // "apple" and "orange" are part
out int orange; // of stream 1.
layout (stream=3) out MY_BLOCK { // Everything in "MY_BLOCK" is instream 3.
vec3 purple;
vec3 green;
};
在几何着色器中,使用过函数EmitVertex()和函数EndPrimitive()操作的都是对于输出流0的。使用函数EmitStreamVertex()和函数EndStreamPrimitive()都可以使用整形参数指定操作的输出流。
2.7 几何着色器中的新图元类型(New Primitive Types Introduced by the Geometry Shader)
几何着色器中引用了4个新的图元类型,GL_LINES_ADJACENCY,GL_LINE_STRIP_ADJACENCY,GL_TRIANGLES_ADJACENCY,和GL_TRIANGLE_STRIP_ADJACENCY。只有几何着色器被激活时,这几个图元才是有效的。当这些新的临近图元被使用后,对于每个传入几何着色器的线或者三角形,我们不仅可以获得当前处理的图元顶点信息,还能获取到该图元的临近图元的顶点数据。
当使用GL_LINES_ADJACENCY图元渲染时,属性数组中每4个顶点组成一个线图元。中间两个顶点组成了当前线图元,前后的顶点时其相邻的线图元的顶点。因此传入几何着色器的输入数组包含4个成员。几何着色器的输入图元和输出图元类型并无关系,我们甚至可以使用这四个顶点生成两个三角形图元。基于这个特性,我们甚至可以使用GL_LINES_ADJACENCY图元类型去渲染矩形。需要注意的是,在几何着色器未被激活时使用GL_LINES_ADJACENCY渲染模型,只有中间两个顶点会被渲染到屏幕上,顶点着色器会直接忽略前后两个顶点。
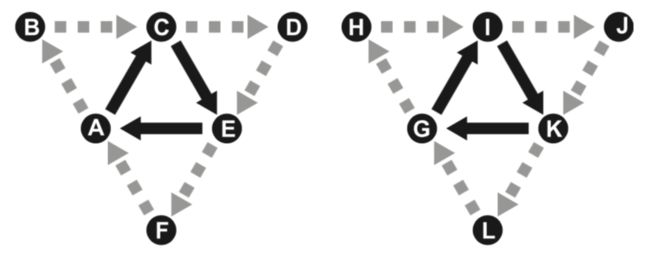
使用GL_LINE_STRIP_ADJACENCY类型图元会出现相似的结果。不同的是整个三角形条带被认为是一个图元,在整个图元的前部和尾部各包含一个临近图元的顶点。如果使用GL_LINES_ADJACENCY类型图元,在渲染管道中放入8个顶点,那么几何着色器将会运行两次,如果使用GL_LINE_STRIP_ADJANCENCY类型图元,几何着色器将会运行5次,详见下图。
对于GL_LINE_STRIP_ADJACENCY类型图元,几何着色器分别处理为ABCD和EFGH两个图元,对于GL_LINE_STRIP_ADJANCENCY类型图元时,会被处理称为ABCD,BCDE直至EFGH。另外在上图中,如果没有几何着色器的加入,只有实线才会被渲染到屏幕上。
GL_TRIANGLES_ADJACENCY类型图元和GL_LINES_ADJACENCY类型图元的工作原理类似。下面讨论6个顶点组成的该图元被发送到几何着色器后的处理过程。第1、3、5个顶点被认为是组成了真实的三角形图元,第2、4、6个顶点被认为是位于三角形之间的顶点。这意味着几何着色器的输入数组包含6个元素。其具体处理逻辑如下图。
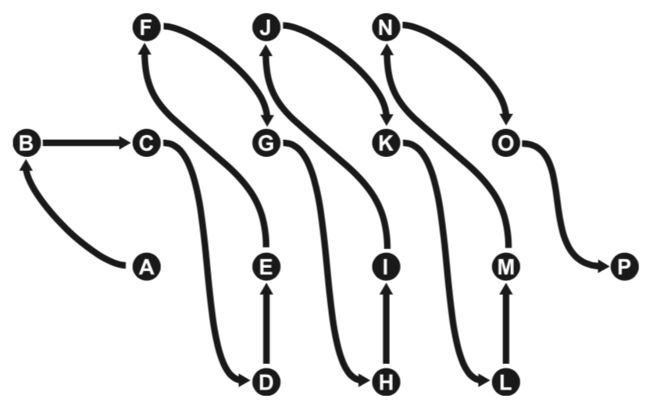
这几个新增图元中最后介绍的一个也是最难的一个(换句话说是最难以理解的)图元类型是GL_TRIANLGLE_STRIP_ADJACENCY。下图形象说明了该类型图元的处理方式。在图中,顶点A到P共16个顶点被传递到了几何着色器,组成三角形条带的顶点之间刚好都间隔1个顶点。
三角形的分割顺序如下图所示,除了头尾两个三角形图元,其他的三角形顶点组合规律都相同。GL_TRIANLGLE_STRIP_ADJACENCY类型图元的顶点组合顺序可以在OpenGL官网中找到详细说明,如果需要使用到该类型图元,最后去阅读相关文档。
使用几何着色器渲染四边形
现代的图像API不直接支持渲染四边形,主要的原因可能是GPU不支持四边形。通常一个模型编辑程序在生成由4边形组成的模型时,都可以选择将其转换为多个三角形。这些图元就能够直接被GPU渲染。部分GPU支持四边形,但是内部也会将四边形转化为多个三角形。
多数情况下,将一个四边形转化为多个三角形的渲染效果和直接渲染四边形的效果在视觉上并不会有太大的区别。但是仍然有很多时候它们的效果并不相同,如下图所示。
在上图中三角形的顶点缠绕方向都相同,另外都包含3个黑色顶点和1个白色顶点,但是左图中,将四边形垂直分割位两个三角形,而在右图中,四边形被水平分割为两个三角形。这导致了左图两个三角形之间有一条明显的高亮缝隙,它直接贯穿了四边形,而右侧四边形上面三角部分都为黑色,而下面部分由黑色向白色过渡。
造成这个现象的原因是,我们分别渲染两个三角形的时候会在单个三角形的顶点中做插值处理,最后将结果传递给片段着色器。而在渲染单个三角形的时候,几何着色器中1次只能获取到三个顶点数据,因此我们不能考虑到四边形中的另外一个顶点数据。
很明显它们都不是我们想要的结果,如果我们依赖于导出工具甚至更糟糕的去依赖于一个运行时库,这样分割的三角形我们不能够控制我们将得到上面的图片中的那一张。那我们能做些什么呢?前面讲过几何着色器可以接受GL_LINES_ADJACENCY类型的图元,并且其中的每个图元都包含四个顶点,这样就足够去描述一个三角形。这也意味着,使用临近线图元类型,我们也能得到足够的信息。
接下来,我们需要处理光栅化器。前面讲过,几何着色器的输出只能是点、线和三角形图元,因此我们最好的方式是将每个四边形(使用lines_adjacency类型图元表示)分组一组三角形。你可能会想这又回到了前面两个三角形的老路,但是这种处理方式我们的优势是能够传递任意我们想要的信息给片段着色器。
为了正确的渲染一个四边形,我们必须将我们将要进行颜色插值(也可以是其他属性的插值)的区域参数化。对于三角形,我们使用重心坐标系,然而对于四边形,我们使用2维坐标即可。因此我们建立如下坐标系。
四边形坐标化后,其中的每个顶点都可以用一个二位向量表示。我们可以通过平滑插值的方式在四边形中找到任意顶点的向量坐标。对于四边形的四个顶点ABCD,它们用向量表示分别为(0,0)、(0,1)、(1,0)和(1,1)。我们可以在几何着色器中为每个顶点计算其向量值,然后再将它们传递给片段着色器。
为了使用向量去追溯其他片段的插值结果,我们做如下观察,使用向量的x值使得插值可以分别在AB和CD边上平滑进行,同样的在垂直方向上使用y值再进行一次插值计算便可以对四边形内任意一点进行插值计算。
本实例中的几何着色器在生成两个新的三角形图元的时候,为每个顶点附加四边形四个顶点的颜色数据,并将其定义为flat类型,指定该属性在经过光栅化器的时候不会进行插值运算。同时将每个顶点位于四边形内的坐标作为一个普通变量传递给片段着色器。这样在片段着色器内部就可以直接进行插值操作。
几何着色器的代码如下。
#version 410 core
layout (lines_adjacency) in;
layout (triangle_strip, max_vertices = 6) out;
in VS_OUT {
vec4 color;
} gs_in[4];
out GS_OUT {
flat vec4 color[4];
vec2 uv;
} gs_out;
void main() {
gl_Position = gl_in[0].gl_Position;
gs_out.uv = vec2(1.0, 0.0);
EmitVertex();
gl_Position = gl_in[1].gl_Position;
gs_out.uv = vec2(0.0, 0.0);
EmitVertex();
gl_Position = gl_in[2].gl_Position;
gs_out.uv = vec2(0.0, 1.0);
// We're only writing the output color for the last
// vertex here because they're flat attributes,
// and the last vertex is the provoking vertex by default
gs_out.color[0] = gs_in[0].color;
gs_out.color[1] = gs_in[1].color;
gs_out.color[2] = gs_in[2].color;
gs_out.color[3] = gs_in[3].color;
EmitVertex();
gl_Position = gl_in[0].gl_Position;
gs_out.uv = vec2(1.0, 0.0);
EmitVertex();
gl_Position = gl_in[2].gl_Position;
gs_out.uv = vec2(0.0, 1.0);
EmitVertex();
gl_Position = gl_in[3].gl_Position;
gs_out.uv = vec2(1.0, 1.0);
gs_out.color[0] = gs_in[0].color;
gs_out.color[1] = gs_in[1].color;
gs_out.color[2] = gs_in[2].color;
gs_out.color[3] = gs_in[3].color;
EmitVertex();
EndPrimitive();
}
片段着色器的代码如下。
#version 410 core
in GS_OUT {
flat vec4 color[4];
vec2 uv;
} fs_in;
out vec4 color;
void main() {
vec4 c1 = mix(fs_in.color[0], fs_in.color[1], fs_in.uv.x);
vec4 c2 = mix(fs_in.color[2], fs_in.color[3], fs_in.uv.x);
color = mix(c1, c2, fs_in.uv.y);
}
最后渲染的结果如下图。本实例的Demo地址为 8.26-gsquads。
2.8 多视口转换(Multiple Viewport Transformations)
前面介绍视口转换的时候提到过使用函数glViewport()和函数glDepthRange()可以指定渲染窗口的大小和深度。通常我们会将视图窗口的尺寸设置为当前程序窗口的大小,这取决于我们的程序是否是在整个程序窗口上运行。此外,我们还可以将单个帧缓存会知道我们虚拟分割的多个窗口中。换句话说,OpenGL允许我们在同一时间将程序窗口分割为多个更小尺寸的虚拟窗口,这个特性被称为视口数组(viewport arrays)。
首先我们需要通知OpenGL我们要分割的窗口大小,可以调用函数void glViewportIndexedf (GLuint index, GLfloat x, GLfloat y, GLfloat w, GLfloat h);和函数void glViewportIndexe dfv (GLuint index, const GLfloat * v);。两个函数中的参数index都表示需要修改的视口索引值。需要注意的是这两个函数中的参数都是GLFLoat类型,和函数glViewport()中的整形参数类型不同。OpenGL最少支持16个视口,因此视口的索引值可以从0递增到15。具体的最大支持视口数量可以通过GL_MAX_VIEWPORTS和相关函数获取。
同样的,每个视口有自己的深度范围,可以使用函数void glDepthRangeIndexed (GLuint index, GLdouble n, GLdouble f);设置。实际上函数glViewport和函数glDepthRange设置了所有视口的尺寸的深度范围。如果想一次设置两个以上的视口尺寸和深度范围,就需要调用函数void glViewportArrayv (GLuint first, GLsizei count, const GLfloat * v);和函数void glDepthRangeArrayv (GLuint first, GLsizei count, const GLdouble * v);。
这两个函数通过第一个视口的索引值first和数量count将多个视口设置为相同的尺寸,此处的大小有数组v指定。对于函数glViewportArrayv,数组v包含4个元素,依次分别为x、y、width和height,对于函数glDepthRangeArrayv,数组v包含两个元素,分别为n和f,即近平面和远平面的距离值。
在指定了视口后需要将几何体分别绘制到各个窗口中,这可以通过几何着色器的多次调用和内置变量gl_ViewportIndex完成。在几何着色器头部文件中声明layout (triangles, invocations = 4) in可以指定为每个图元调用几何着色器的次数,默认是1次。几何着色器代码如下。
#version 410 core
// 在几何着色器内部启用多次调用颜色值不能正确传递进入片段着色器,后续研究
layout (triangles, invocations = 4) in;
layout (triangle_strip, max_vertices = 3) out;
layout (std140) uniform transform_block {
mat4 mvp_matrix[4];
};
in VS_OUT {
vec4 color;
} gs_in[];
out GS_OUT {
vec4 color;
} gs_out;
void main() {
for (int i = 0; i < gl_in.length(); i++) {
gl_Position = mvp_matrix[gl_InvocationID] * gl_in[i].gl_Position;
gs_out.color = gs_in[i].color;
// 在几何着色器内部启用多次调用颜色值不能正确传递进入片段着色器,后续研究
gs_out.color = vec4(1.0);
gl_ViewportIndex = gl_InvocationID;
EmitVertex();
}
EndPrimitive();
}
当上述着色器执行完毕后,该着色器会被调用四次。在每次调用的时候,将内置变量gl_InvocationID赋值为gl_InvocationID,就可以将每个着色器实例的结果引导至不同的视口中。同样的,对于每一个调用,都应用单独的模型-视图-投影矩阵,可以通过统一变量闭包获取。当然,OpenGL允许构建更复杂的着色器,但是本实例已经足够说明如何将多次调用单个几何着色器并将其结果分别输入到多个视口中。该实例的渲染结果如下图,Demo地址为Chapter 8/8.27-multiViewport。 但Demo中的多个立方体都为白色,是因为传递颜色发生未知错误,因此直接指定了白色,暂未发现具体原因,后续继续研究。
3 总结(Summary)
在本章中,学习了曲面细分着色器的2个可编程阶段,不可编程的曲面细分引擎以及它们的交互方式。此外还学习了几何着色器,同时了解了曲面细分着色器和几何着色器如何组合在一起用于改变OpenGL渲染管道中的顶点数量。此外还介绍了在曲面细分着色器和几何着色器中可以使用的一些特性。另外介绍了曲面细分着色器和几何着色器如果将顶点分组处理,在曲面细分着色器中,这些分组构成了图块(patches),在几何着色器中这些分组构成了如线和三角形等传统图元。此外,介绍了一组需要几何着色器才能生效的图元类型adjacency。在几何着色器后,图元最终被传递给光栅化器,然后再处理每个片段,这将是下一个章节讨论的内容。