林轩田的机器学习基石课程
1-3讲主要是讲机器学习应该使用在什么地方,机器学习有哪些分类.
4-8讲主要机器凭什么能学到东西(机器怎样的表现才是学到了东西)
这篇文章主要回顾一下4-8讲中机器怎样的表现才表明机器学到了东西。
这里我们不讲每一讲说的内容详情,适合已经看完1-8的同学,隔了有一段时间,把内容忘记了,可以在这进行回顾。
需要看详细每一讲的讲解,我看过好多同学的博客记录,Tingxun的博客记录得非常好
http://txshi-mt.com/categories/%E7%BB%9F%E8%AE%A1%E6%9C%BA%E5%99%A8%E5%AD%A6%E4%B9%A0/
从第四讲开始就把霍夫丁不等式提出来,在之后的几讲中都是围绕着这个不等式去展开的,下面先给出这个霍夫丁不等式:
其所描述的就是估计值比真值大”多少”的概率被指数边界控制
霍夫丁不等式经常被应用于一些独立分布的伯努利随机变量的重要特例中,这也是为什么这个不等式在计算机科学以及组合数学中如此常见。我们认为一个抛硬币时一个硬币A面朝上的概率为p,B面朝上的概率则为1-p。我们抛n次硬币,那么A面朝上次数的期望值为np。那么进一步我们可以知道,A面朝上的次数不超过k次的概率能够被下面的表达式完全确定:
这里的H(n)为抛n次硬币其A面朝上的次数。
对某一ε>0,当k=(p-ε)n时,上面不等式确定的霍夫丁上界将会按照指数级变化:
相似的,对某一ε>0,当k=(p+ε)n,霍夫丁不等式的概率边界同样可以确定为:
这样根据上面两个式子我们可以得到:
以上是霍夫丁不等式的一些应用,或者说是一些变形
回到课程中:
霍夫丁不等式第一次出现时是长这样子:
我们从瓶子中抽取一把弹珠,这个流程是独立同分布的(i.i.d),而且样本只有两种可能,就是橙色弹珠和绿色弹珠.我们就会有以下的
ν是抽样出来的橙色弹珠的概率 ---也就是我们的期望值(估值)
μ是瓶子中橙色弹珠的概率---也就是红色弹珠的真实概率值(真值)
ε是我们设定的一个阔值,也能说是一个距离
N是从瓶子中抓取出来的弹珠的数量
|ν-μ|是ν和μ相减得出的结果的绝对值
|ν-μ|>ε 计算出来的值会比设定的一个阔值大
P(|ν-μ|>ε) 计算出来的值会比设定的一个阔值大的概率
计算出来的值比一个以e为底负指数的数,(可以看出是一个很小的数)。
第二次变化:
用到了“瓶子中取样”跟“机器学习h(x)预测”进行比较
1.“瓶子取样”:我们不知道的东西是瓶子里的橙色弹珠的比例,
“机器学习中:我们不知道的是目标函数f(x),比如说,是否发信用卡问题,我们不知道原有的一个公式。
2.“瓶子中取样”:我们看出橙色的弹珠在样本中占的比例。
“机器学习中”:现在我们有一个h(x),瓶子中每一颗弹珠,都可以看做为一个x,
我们从瓶子中抓一把就有一把的Data{(xn,yn)},我们用已知的h(x)去检验
h(xn)≠yn(也就是橙色的弹珠)占的比例。
3.“瓶子取样”:从取样出来橙色弹珠的比例,我们就能知道瓶子中橙色弹珠的比例。
“机器学习”:我们用h(x)去检验取出来的样本,也能得知橙色弹珠比例,也能知道未知的f(x)大概也是这样。
然后我们就得出了这一条
Ein:我们知道的数据的错误率(估值)
Eout: 我们未知的f(x)的错误率(真值)
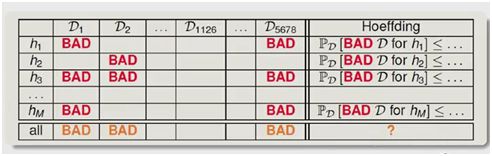
前面说到假说h1,h2,h3……hi,这些假说可能会相交
对于概率的公式:P(AUB)=P(A)+P(B)有条件限制:如果A和B没有交集,就是互逆事件的时候.这个答案是对的
如果A和B有交集,就表示,P(AUB)≧P(A)+P(B)
这里我们得出了M
M是h的个数,假设空间平面上h是一条线,我们会有无数条线,M是∞的,我们现在试试找一个mh(N)去替换M。
我们的数据是有限的,记做N。
相邻很近的h,其实是很相似的,我们可以用有限的数据将无限的h去分类,分成mh(N)类。
我们就可以用mh(N)去替换M。
就有下面的:
成立
第六、七讲都是一般理论化,做证明,最后得出了这个:
最后,得出了,我们要让机器学习到东西,
我们给出ε、δ、dvc的值,猜想需要的资料数,代入公式
[endif]求的出来的数是否≦δ
但这里说通常不需要那么多的数据,一般来说dvc*10,就足够了,因为有很多条件上界去界限了。