- 关于中如何编辑Latex数学公式
- [RNN] Simple LSTM代码实现 & BPTT理论推导
【知识预备】: UFLDL教程 - 反向传导算法
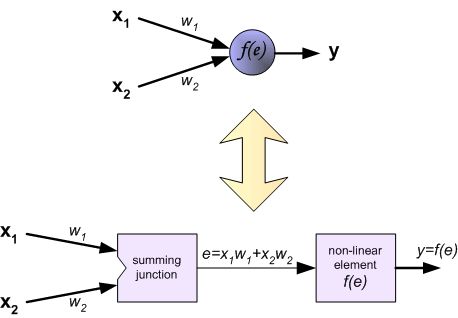
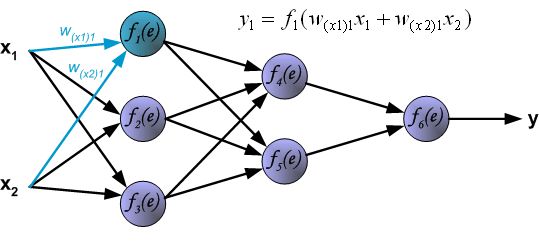
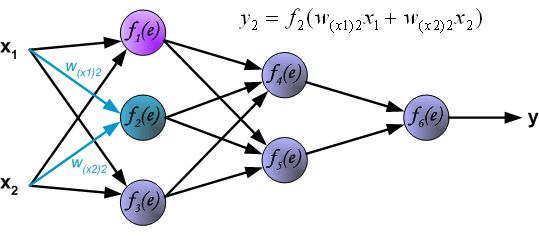
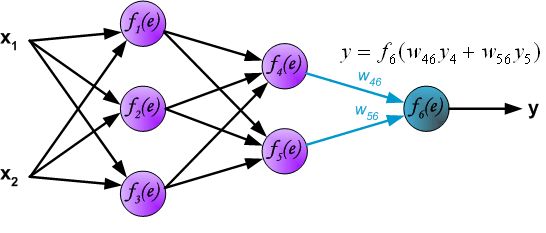
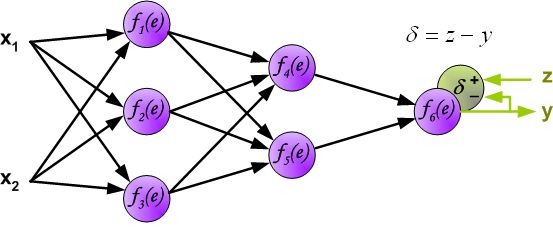
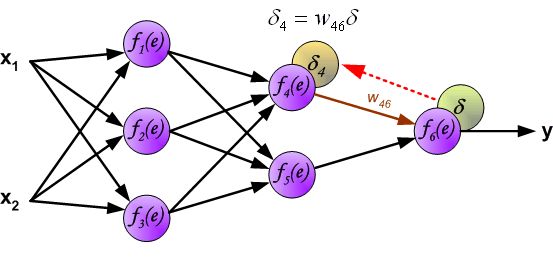
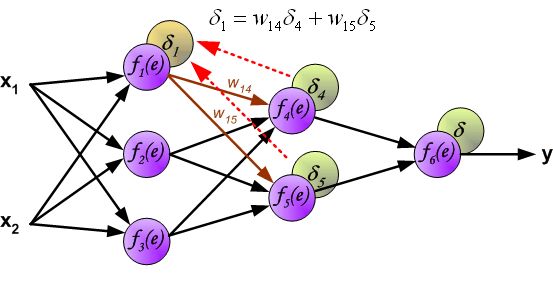
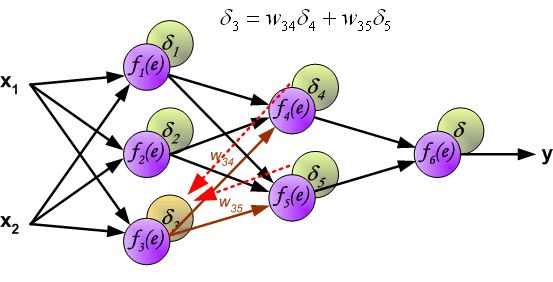
首先我们不讲数学,先上图解,看完图不懂再看后面:
"BP" Math Principle
======================================================================
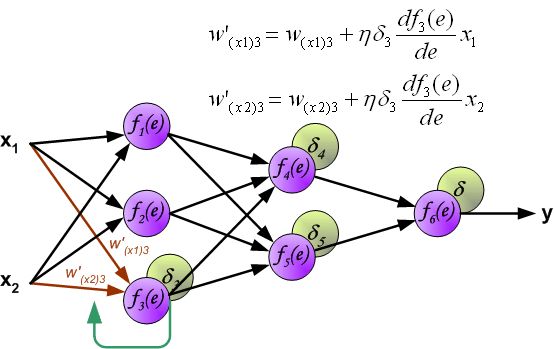
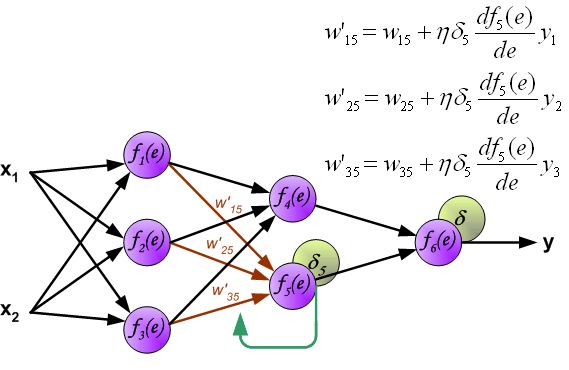
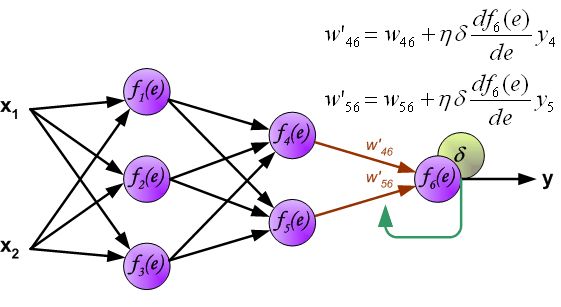
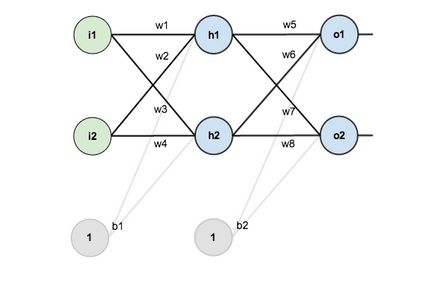
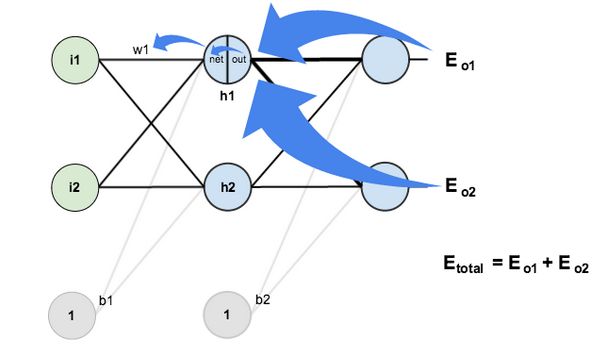
Example:下面看一个简单的三层神经网络模型,一层输入层,一层隐藏层,一层输出层。
注:定义输入分别为x1, x2(对应图中的i1,i2),期望输出为y1,y2,假设logistic函数采用sigmoid函数:
![][40]
[40]:http://latex.codecogs.com/png.latex?y%20=%20f(x)=sigmoid(x)%20=\frac{1}{1%20+%20e^{-x}}
易知:
![][00]
[00]:http://latex.codecogs.com/png.latex?f%27(x)%20=%20f(x)%20*%20(1%20-%20f(x))
下面开始正式分析(纯手打!!!)。
======================================================================
前向传播
首先分析神经元h1:
![][01]
[01]:http://latex.codecogs.com/png.latex?input_{(h1)}%20=%20w1%20%20x1%20+%20w2%20%20x2%20+%20b1
![][02]
[02]:http://latex.codecogs.com/png.latex?output_{(h1)}%20=%20f(input_{(h1)})%20=%20\frac{1}{1%20+%20e^{-(w1x1+w2x2+b1)}}
同理可得神经元h2:
![][03]
[03]:http://latex.codecogs.com/png.latex?input_{(h2)}%20=%20w3%20%20x1%20+%20w4%20%20x2%20+%20b1
![][04]
[04]:http://latex.codecogs.com/png.latex?output_{(h2)}%20=%20f(input_{(h2)})%20=%20\frac{1}{1%20+%20e^{-(w3x1+w4x2+b1)}}
对输出层神经元重复这个过程,使用隐藏层神经元的输出作为输入。这样就能给出o1,o2的输入输出:
![][05]
[05]:http://latex.codecogs.com/png.latex?input_{(o1)}%20=%20w5%20%20output_{(h1)}%20+%20w6%20%20output_{(h2)}%20+%20b2
![][06]
[06]:http://latex.codecogs.com/png.latex?output_{(o1)}%20=%20f(input_{(o1)})
![][07]
[07]:http://latex.codecogs.com/png.latex?input_{(o2)}%20=%20w7%20%20output_{(h1)}%20+%20w8%20%20output_{(h2)}%20+%20b2
![][08]
[08]:http://latex.codecogs.com/png.latex?output_{(o2)}%20=%20f(input_{(o2)})
现在开始统计所有误差,如下:
![][09]
[09]:http://latex.codecogs.com/png.latex?J_{total}%20=%20\sum%20\frac{1}{2}(output%20-%20target)^2%20=%20J_{o1}+J_{o2}
![][10]
[10]:http://latex.codecogs.com/png.latex?J_{o1}%20=%20\frac{1}{2}(output(o1)-y1)^2
![][11]
[11]:http://latex.codecogs.com/png.latex?J_{o2}%20=%20\frac{1}{2}(output(o2)-y2)^2
======================================================================
反向传播
【输出层】
对于w5,想知道其改变对总误差有多少影响,于是求Jtotal对w5的偏导数,如下:
![][12]
[12]:http://latex.codecogs.com/png.latex?\frac{\partial%20J_{total}}{\partial%20w5}=\frac{\partial%20J_{total}}{\partial%20output_{(o1)}}\frac{\partial%20output_{(o1)}}{\partial%20input_{(o1)}}\frac{\partial%20input_{(o1)}}{\partial%20w5}
分别求每一项:
![][13]
[13]:http://latex.codecogs.com/png.latex?\frac{\partial%20J_{total}}{\partial%20output_{(o1)}}=\frac{\partial%20J_{o1}}{\partial%20output_{(o1)}}=output_{(o1)}-y_1
![][14]
[14]:http://latex.codecogs.com/png.latex?\frac{\partial%20output_{(o1)}}{\partial%20input_{(o1)}}%20=%20f%27(input_{(o1)})=output_{(o1)}*(1%20-%20output_{(o1)})
![][15]
[15]:http://latex.codecogs.com/png.latex?\frac{\partial%20input_{(o1)}}{\partial%20w5}=\frac{\partial%20(w5%20%20output_{(h1)}%20+%20w6%20%20output_{(h2)}%20+%20b2)}{\partial%20w5}=output_{(h1)}
于是有Jtotal对w5的偏导数:
![][16]
[16]:http://latex.codecogs.com/png.latex?\frac{\partial%20J_{total}}{\partial%20w5}=(output_{(o1)}-y1)[output_{(o1)}(1%20-%20output_{(o1)})]*output_{(h1)}
据此更新权重w5,有:
![][17]
[17]:http://latex.codecogs.com/png.latex?w5^+%20=%20w5%20-%20\eta*\frac{\partial%20J_{total}}{\partial%20w5}
同理可以更新参数w6,w7,w8。
在有新权重导入隐藏层神经元(即,当继续下面的反向传播算法时,使用原始权重,而不是更新的权重)之后,执行神经网络中的实际更新。
【隐藏层】
对于w1,想知道其改变对总误差有多少影响,于是求Jtotal对w1的偏导数,如下:
![][18]
[18]:http://latex.codecogs.com/png.latex?\frac{\partial%20J_{total}}{\partial%20w1}=\frac{\partial%20J_{total}}{\partial%20output_{(h1)}}\frac{\partial%20output_{(h1)}}{\partial%20input_{(h1)}}\frac{\partial%20input_{(h1)}}{\partial%20w1}
分别求每一项:
![][19]
[19]:http://latex.codecogs.com/png.latex?\frac{\partial%20J_{total}}{\partial%20output_{(h1)}}=\frac{\partial%20J_{o1}}{\partial%20output_{(h1)}}+\frac{\partial%20J_{o2}}{\partial%20output_{(h1)}}
![][20]
[20]:http://latex.codecogs.com/png.latex?\frac{\partial%20J_{o1}}{\partial%20output_{(h1)}}=\frac{\partial%20J_{o1}}{\partial%20output_{(o1)}}\frac{\partial%20output_{(o1)}}{\partial%20input_{(o1)}}\frac{\partial%20input_{(o1)}}{\partial%20output_{(h1)}}
![][21]
[21]:http://latex.codecogs.com/png.latex?=(output_{(o1)}-y1)[output_{(o1)}(1%20-%20output_{(o1)})]*w5
![][22]
[22]:http://latex.codecogs.com/png.latex?\frac{\partial%20J_{o2}}{\partial%20output_{(h1)}}=\frac{\partial%20J_{o2}}{\partial%20output_{(o2)}}\frac{\partial%20output_{(o2)}}{\partial%20input_{(o2)}}\frac{\partial%20input_{(o2)}}{\partial%20output_{(h1)}}
![][23]
[23]:http://latex.codecogs.com/png.latex?=(output_{(o2)}-y2)[output_{(o2)}(1%20-%20output_{(o2)})]*w7
![][24]
[24]:http://latex.codecogs.com/png.latex?\frac{\partial%20output_{(h1)}}{\partial%20input_{(h1)}}%20=%20f%27(input_{(h1)})=output_{(h1)}*(1%20-%20output_{(h1)})
![][25]
[25]:http://latex.codecogs.com/png.latex?\frac{\partial%20input_{(h1)}}{\partial%20w1}=\frac{\partial%20(w1%20%20x1%20+%20w2%20%20x2%20+%20b1)}{\partial%20w1}=x1
于是有Jtotal对w1的偏导数:
![][26]
[26]:http://latex.codecogs.com/png.latex?\frac{\partial%20J_{total}}{\partial%20w1}={(output_{(o1)}-y1)[output_{(o1)}(1%20-%20output_{(o1)})]*w5
![][27]
[27]:http://latex.codecogs.com/png.latex?+%20(output_{(o2)}-y2)[output_{(o2)}(1%20-%20output_{(o2)})]w7}
![][28]
[28]:http://latex.codecogs.com/png.latex?[output_{(h1)}(1%20-%20output_{(h1)})]x1
据此更新w1,有:
![][29]
[29]:http://latex.codecogs.com/png.latex?w1^+%20=%20w1%20-%20\eta*\frac{\partial%20J_{total}}{\partial%20w1}
同理可以更新参数w2,w3,w4。
======================================================================
应用实例
假设对于上述简单三层网络模型,按如下方式初始化权重和偏置:
根据上述推导的公式:
由
![][01]
得到:
input(h1) = 0.15 * 0.05 + 0.20 * 0.10 + 0.35 = 0.3775
output(h1) = f(input(h1)) = 1 / (1 + e^(-input(h1))) = 1 / (1 + e^-0.3775) = 0.593269992
同样得到:
input(h2) = 0.25 * 0.05 + 0.30 * 0.10 + 0.35 = 0.3925
output(h2) = f(input(h2)) = 1 / (1 + e^(-input(h2))) = 1 / (1 + e^-0.3925) = 0.596884378
对输出层神经元重复这个过程,使用隐藏层神经元的输出作为输入。这样就能给出o1的输出:
input(o1) = w5 * output(h1) + w6 * (output(h2)) + b2 = 0.40 * 0.593269992 + 0.45 * 0.596884378 + 0.60 = 1.105905967
output(o1) = f(input(o1)) = 1 / (1 + e^-1.105905967) = 0.75136507
同理output(o2) = 0.772928465
开始统计所有误差,求代价函数:
Jo1 = 1/2 * (0.75136507 - 0.01)^2 = 0.298371109
Jo2 = 1/2 * (0.772928465 - 0.99)^2 = 0.023560026
综合所述,可以得到总误差为:Jtotal = Jo1 + Jo2 = 0.321931135
然后反向传播,根据公式
![][16]
求出 Jtotal对w5的偏导数为:
a = (0.75136507 - 0.01)*0.75136507*(1-0.75136507)*0.593269992 = 0.082167041
为了减少误差,然后从当前的权重减去这个值(可选择乘以一个学习率,比如设置为0.5),得:
w5+ = w5 - eta * a = 0.40 - 0.5 * 0.082167041 = 0.35891648
同理可以求出:
w6+ = 0.408666186
w7+ = 0.511301270
w8+ = 0.561370121
对于隐藏层,更新w1,求Jtotal对w1的偏导数:
![][26]
![][27]
![][28]
偏导数为:
b = (tmp1 + tmp2) * tmp3
tmp1 = (0.75136507 - 0.01) * [0.75136507 * (1 - 0.75136507)] * 0.40 = 0.74136507 * 0.186815602 * 0.40 = 0.055399425
tmp2 = -0.019049119
tmp3 = 0.593269992 * (1 - 0.593269992) * 0.05 = 0.012065035
于是b = 0.000438568
更新权重w1为:
w1+ = w1 - eta * b = 0.15 - 0.5 * 0.000438568 = 0.149780716
同样可以求得:
w2+ = 0.19956143
w3+ = 0.24975114
w4+ = 0.29950229
最后,更新了所有的权重! 当最初前馈传播时输入为0.05和0.1,网络上的误差是0.298371109。 在第一轮反向传播之后,总误差现在下降到0.291027924。 它可能看起来不太多,但是在重复此过程10,000次之后。例如,错误倾斜到0.000035085。
在这一点上,当前馈输入为0.05和0.1时,两个输出神经元产生0.015912196(相对于目标为0.01)和0.984065734(相对于目标为0.99),已经很接近了O(∩_∩)O~~
Reference
- https://zhuanlan.zhihu.com/p/23270674
- Principles of training multi-layer neural network using backpropagation
- [RNN] Simple LSTM代码实现 & BPTT理论推导
- 中如何编辑Latex数学公式
(注:感谢您的阅读,希望本文对您有所帮助。如果觉得不错欢迎分享转载,但请先点击 这里 获取授权。本文由 版权印 提供保护,禁止任何形式的未授权违规转载,谢谢!)