图像纹理合成及纹理传输算法学习（附源码）。

    有2到3年没有逛CodeProject了，上班一时无聊，就翻翻这个比较有名的国外网站，在其Articles » Multimedia » General Graphics » Graphics一栏看到exture Transfer using Efros & Freeman's Image Quilting Algorithm顿感兴趣，其效果很有特色，又激起了我好久没写代码的心，想想在这个算法上大概前前后后思索了1个多星期，虽然最终还是没有得到我想要的结果，但并不全无收获，至此国庆佳节加班之际抽空总结一下，以便慰藉我孤独的心灵。

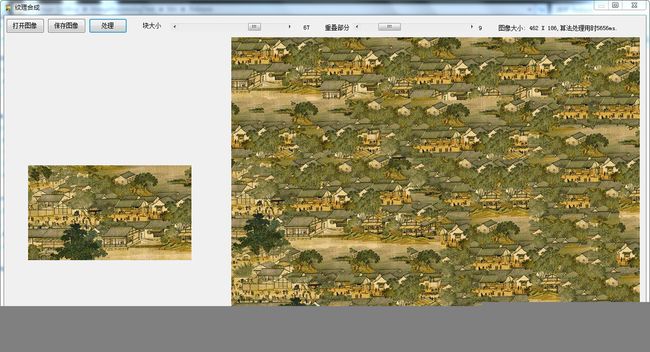
    纹理图像的合成算法在早期的Photoshop中我记得是有一个单独的功能的，在后来的版本中不知道为什么被取消了，印象中他能将只有几颗小草的图片生长成很多小草，并且基本看不出什么瑕疵和不自然的地方，那么CodeProject上的这个Quilting算法也有类似的能力，首先贴几张处理的结果图欣赏一下。

                                            

      

 

        

　　　　原始纹理图像　　　　　　　　　　　　　　　　　　　　　　　         　由小纹理合成的大纹理图像

    那么简单的描述下这篇文章所使用的算法的过程吧。

    算法需要的输入：原始的纹理图像(W * H)，块的大小TileSize，重叠部分的大小Overlap。

　 第一步：我们从原始的纹理图像中一个随机的抽取一个小块，放到目标图像的左上角。

           

    无需解释，其中黑色的部分表示目标图像尚未处理的部分。

    第二步：按照从左到右，从上到下，抽取出块重叠的部分的数据，并计算这部分数据和原始纹理图像中各块的相似度。

                  

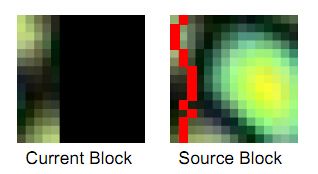
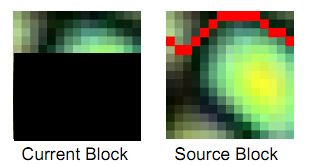
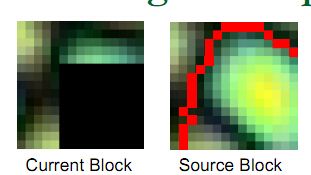
                水平重叠                                   垂直重叠                         水平和垂直部分具有重叠

　　要达到合成自然，在有了第一个块之后，其周边的块应该从原图中选择和其最相似的部位， 因此 ，我们从已经合成的块中抽取部分重叠的数据，如上图所示，红色方框内，没有红色网格线的部分即为重叠的内容，在整个的处理过程中，会有三种情况出现，分别如上图所示,即（1）只有垂直方向有部分重叠；（2）只有水平发方向有部分重叠；（3）水平和垂直方向都有重叠。

    为了选择合适的下一个块，我们结算这些重叠的块和原图中的所有块的相似度，块和块之间的相似度可以有很多准则计算，最常用的莫过于SSD(Sum of Squared Distance)，这里我们也采用这种准则。

　　对于第一种只有垂直方向有部分重叠的情况，块的可能性有 （W - Overlap）* （H - TileSize）种，而只有水平发方向有部分重叠时，块的可能性有（W - TileSize)* (H - Overlap)种，当水平和垂直方向都有重叠时，只有（W - TileSize）* （H - TileSize）种块的选择方案。

    对于水平和垂直有交叉的情况，需要分别计算水平重叠的相似性A，垂直重叠的相似性B以及交叉部位的相似性AB，最终的相似性由A + B - AB决定。

    计算完相似性后，一般情况下，我们可取相似度最小的块为下一个块，当然为了随机性更强，也可以取相似性序列中前N个最小值种的某个块为选中的块。

    第三步：如果对选中的块直接进行拼贴到目标图中，则很明显两个块之间由过渡不会太自然，一种较好的方式就是在选中的块和重叠的部分找到一条路径，在该路径的两侧像素的距离和最小，如果使用暴力的方式去寻找这条路径，则是非常耗时和不必要的，文章介绍使用了贪心算法来寻找这条路径。

    我们拿水平重叠的块来说明问题，首先找到第一行最小距离和的像素的位置，假定为(x,1),接着我们搜索第二行的（x - 1, 2), （x, 2), （x + 1, 2)三个位置的距离和的最小值，假定是 （x - 1, 2)是第二行的最小值，则第三行需要搜索的位置为（x - 2, 3), （x - 1, 3), （x, 3)，依类类推直到最后一行。

    其实路径必然是连续的，因此这种只搜索向下的三领域的做法是完全合理的。

    一般情况下，做图像算法会按照从左到右，从上到下的顺序进行处理，这样能够充分利用cache line的优势，如果按照从上到下，然后在从左到右的方式来处理，虽然逻辑和结果是一样的，通常会需要更多的时间，因此，在计算垂直的块的路径时，我们可以借用水平块的算法，只要对垂直的块的数据先进行转置，处理转置的数据得到对应的数据，然后在把这个数据转置就得到了垂直块的结果。注意这里是用的转置，而不是旋转，因为旋转对于该问题是的到的结果是镜像的，所以必须注意。

    在水平和垂直部分具有重叠的块的计算时，我们是分别计算垂直和水平的路径，然后取两个路径的交集，计算过程分别如下图。

  

    第四步： 按照路径的位置贴入新的数据。

    编程技巧：

    （1） 在整个的计算中，计算SSD是最为耗时的，因此对其优化是调高程序效率的关键。

 　　我们看一段matlab的代码，如下所示：

%function Z = ssd(X, Y)
%Computes the sum of squared distances between X and Y for each possible
% overlap of Y on X.  Y is thus smaller than X
%
%Inputs:
%   X - larger image
%   Y - smaller image
%
%Outputs:
%   Each pixel of Z contains the ssd for Y overlaid on X at that pixel

function Z = ssd(X, Y)

K = ones(size(Y,1), size(Y,2));

for k=1:size(X,3),
    A = X(:,:,k);
    B = Y(:,:,k);
    
    a2 = filter2(K, A.^2, 'valid');
    b2 = sum(sum(B.^2));
    ab = filter2(B, A, 'valid').*2;

    if( k == 1 )
        Z = ((a2 - ab) + b2);
    else
        Z = Z + ((a2 - ab) + b2);
    end;
end;

　　这里的优化时通过卷积实现的，因为SSD的计算就是(a-b)^2的累积和，展开为a^2 + b^2 - 2ab，其中a为固定的图像，那么a^2则为一定值，b^2是不断变化的，但是也可以用积分图之类的算法实现快速效果，唯一的耗时时2ab项，可以用卷积来实现。

     快速的卷积算法可以通过FFT来实现，也可以借鉴我在图像处理中任意核卷积(matlab中conv2函数)的快速实现 一文中提到的用SSE的方式实现，鉴于这里的卷积更有其特殊性，他是2幅图像之间的卷积，因此参与计算的都是byte类型，则可以通过选择更为合适的SSE函数来进一步提高效率，这里要感谢有关高手提供的一段SSE代码。

/// 

/// 基于SSE的字节数据的乘法。
/// 
/// 需要卷积的核矩阵。
/// 卷积矩阵。
/// 矩阵所有元素的长度。
///  1: 使用了SSE优化。
///  2: 感谢采石工（544617183）提供的SSE代码<。
///    https://msdn.microsoft.com/zh-cn/library/t5h7783k(v=vs.90).aspx

int MultiplySSE(unsigned char* Kernel, unsigned char * Conv, int Length)
{
    int Y, Sum;
    __m128i vsum = _mm_set1_epi32(0);
    __m128i vk0 = _mm_set1_epi8(0);
    for (Y = 0; Y <= Length - 16; Y += 16)
    {
        __m128i v0 = _mm_loadu_si128((__m128i*)(Kernel + Y));                //    对应movdqu指令,不需要16字节对齐
        __m128i v0l = _mm_unpacklo_epi8(v0, vk0);                            
        __m128i v0h = _mm_unpackhi_epi8(v0, vk0);                            //    此两句的作用是把他们分别加载到两个128位寄存器中，供下面的_mm_madd_epi16的16位SSE函数调用（vk0的作用主要是把高8位置0）                
        __m128i v1 = _mm_loadu_si128((__m128i*)(Conv + Y));
        __m128i v1l = _mm_unpacklo_epi8(v1, vk0);
        __m128i v1h = _mm_unpackhi_epi8(v1, vk0);
        vsum = _mm_add_epi32(vsum, _mm_madd_epi16(v0l, v1l));                //    _mm_madd_epi16 可以一次性进行8个16位数的乘法，然后把两个16的结果在加起来，放到一个32数中， r0 := (a0 * b0) + (a1 * b1)，详见 https://msdn.microsoft.com/zh-cn/library/yht36sa6(v=vs.90).aspx
        vsum = _mm_add_epi32(vsum, _mm_madd_epi16(v0h, v1h));
    }
    for (; Y <= Length - 8; Y += 8)
    {
        __m128i v0 = _mm_loadl_epi64((__m128i*)(Kernel + Y));
        __m128i v0l = _mm_unpacklo_epi8(v0, vk0);
        __m128i v1 = _mm_loadl_epi64((__m128i*)(Conv + Y));
        __m128i v1l = _mm_unpacklo_epi8(v1, vk0);
        vsum = _mm_add_epi32(vsum, _mm_madd_epi16(v0l, v1l));
    }
    vsum = _mm_add_epi32(vsum, _mm_srli_si128(vsum, 8));
    vsum = _mm_add_epi32(vsum, _mm_srli_si128(vsum, 4));
    Sum = _mm_cvtsi128_si32(vsum);                                            //    MOVD函数，Moves the least significant 32 bits of a to a 32-bit integer：   r := a0

    for ( ; Y < Length; Y++)
    {
        Sum += Kernel[Y] * Conv[Y];
    }
    return Sum;
}

      以上代码在大数据量时可以一次性完成16个字节数据的乘法及累加，大大的提高了效率。

      以上计算SSD的方式也可以帮助提高标准的模板匹配算法的速度，这个我想有心的人应该不难实现。

      但是即使采用了这种快速的计算，整个纹理合成的速度还是相当的慢，要使得该算法具有实际的实用价值，还的寻找快速的块相似度平价方法。

      由于程序速度问题，我对纹理传输的编写已经失去了信心，纹理传输过程总的和纹理合成和类似，只是在计算相似度时还要考虑目标的诸如亮度或者模糊只方面的信息，速度会比这个纹理合成还要慢，有兴趣的朋友可以看看我提供的一些链接，里面基本都有参考代码。

　　不过纹理传输产生的效果有的时候确实比较酷：

      

    

      那天心血来潮我还是去实现下这个效果吧。

      纹理合成完整的工程下载：

      http://files.cnblogs.com/files/Imageshop/ImageQuilting.rar

 

 参考资料：

http://web.engr.illinois.edu/~vrgsslv2/cs498dwh/proj2/

http://www.codeproject.com/Articles/24172/Texture-Transfer-using-Efros-Freeman-s-Image-Quilt

http://mesh.brown.edu/dlanman/courses.html

 

 

****************************作者： laviewpbt   时间： 2015.10.1    联系QQ:  33184777 转载请保留本行信息**********************