俄罗斯方块

   

 

 

　　

　　小时候，每天放学回到家，急冲冲写完家庭作业，然后我就搬出游戏机，开始打游戏。对于 80 后而言，“ 游戏机 ” 这三个字是一个不言自明的符号，那就是经典的任天堂红白机，还有一盘盘可以代表幸福指数的游戏卡。当年谁家的小朋友拥有的游戏卡多，谁就是当时的红人，尤其是黑卡，简直是高端的象征。

　

 

　　得益于父母开明，打游戏这事我没受过限制，又得益于我有个伟大的表哥，所以我的幸福指数也从来都是在高位震荡。经典的《魂斗罗》《坦克大战》《绿色兵团》《赤色要塞》《热血系列》等，冷门的《惩罚者》《圣斗士》《电梯》等等，包括后来玩的文卡《三国志》，虽不敢说天下游戏玩了个遍，但也是见过世面的资深玩家了。

　　父亲虽然不限制我，却常会唠叨“作业做完了就多看看课外书，少玩游戏。打游戏浪费时间。” 经常对着我正在玩的《热血足球》说：“你要踢球就下楼去踢，操作几个娃娃人在电视上踢有什么意思？而且你这都是些什么乱七八糟的，还有星星？！”（玩过热血足球的应该都知道此刻屏幕上“小辫子”正在放大招）。

　　但是，父亲有时候也会和我一起玩，很投入地玩，而且永远只玩一个游戏——《俄罗斯方块》。

 

 

　　无数个周末下午，我和父亲就是在对战俄罗斯方块中度过的。

　　这款游戏，对于我而言，有着很深刻的印象，它承载着童年，也承载着父子之情。

 　

　

　　《俄罗斯方块》(Tetris) 诞生于 1984 年 6 月 6 日。当时在前苏联科学院电算中心工作的科学家 阿列克谢-帕基特诺夫 利用空闲时间设计和编写了这个落下型益智游戏的始祖。按理说，这款游戏其实应该叫做 “前苏联方块”。

　　这款冷战时期的产物，成了第一个进入美国的苏联游戏。后来还被评为“最伟大的100个游戏”中的第1名、Gome Boy 史上最受欢迎的游戏、有史以来最畅销的电子游戏，荣誉太多了。

 

　　当年初学 C# 时，觉得用 Winform 做点小玩意很快乐，曾想自己做一个俄罗斯方块。但一想到“方块旋转”，“碰撞检测”，“GDI+ 动画”等等具体问题，就一头雾水，感觉难度太大，于是就放弃了。

　　一放就是好多年。

　　前不久，忽然有一天，也说不上来什么原因，又想到了俄罗斯方块，又萌生了自己动手写一个的念头。可能这就是所谓的童年的影响所带来的执念，不论过多久，总有个牵挂在心里。

　　念头来得容易，但问题依然存在，还是得想办法解决旋转、碰撞、动画等实际问题。

　　鉴于我的早年经历，用 C# 来做这事的话，首先就想到 GDI+ ，可我以前学 GDI+ 时就没有学好，这么多年过去了，更不会了。我也不从事游戏开发领域，对于动画，尤其是处理图形变换、碰撞检测这样的概念，缺乏相关知识储备。

　　再一次感到束手无策。

　　于是我游离了。

　　倒也没游多远，在 Wikipedia 上查阅“俄罗斯方块”这个词条，想了解一下游戏的背景。意外地发现了一个有趣的知识：俄罗斯方块的英文名叫做 Tetris， 这个名称来自于希腊数字表示 4 的前缀 "tetra" 和网球 “tennis” ——两个词组合而成。之所以用数字 4 的原因是游戏中的方块元素都是由4个方格组成，而网球则是作者最喜欢的运动。

　　虽然玩了无数遍，但看到这条信息时我才意识到，原来游戏中的那些方块都可以分解成4个小方格组成。

　　而这个意外的收获给了我一个启发：既然每个方块可以方格化，那么扩展一下，整个游戏的构成也可以网格化。

　　瞬间，事情出现了转机。

    

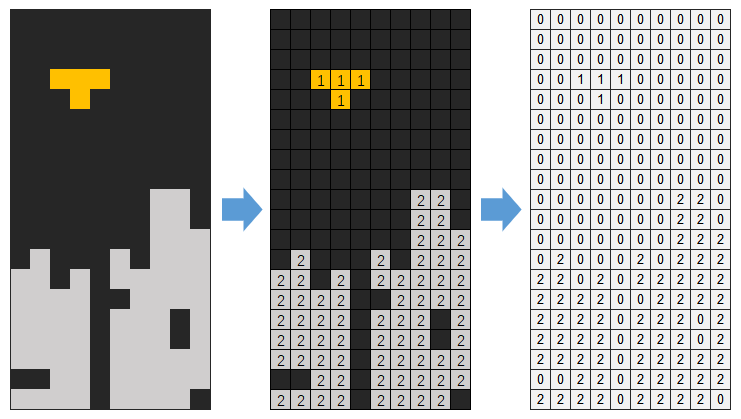
　　俄罗斯方块游戏的视觉呈现可以抽象为两部分：背景空间和方块。

　　将背景空间看成一张表格，方块可以看成是表格中单元格的组合。

　　于是，游戏中任意一个时刻的静态画面，可以抽象成：

　　一张表格中，部分单元格有方块，部分单元格无方块，且每一个单元格只可能处于两种状态中的一种。

　　而游戏的过程就是将所有时刻的静态画面按时间顺序“一帧帧”呈现。 也就是说，所有的视觉效果都可以映射为多次更新一张表格中的不同单元格的状态。    

　　如此一来，之前困扰我的——

　　“图形旋转”就演化成了修改单元格的值。

　　“碰撞检测”就只需要判断单元格的行列位置。

　　至于“GDI+绘图”，就变成了给单元格着色。    

 

　　时间上，将动态过程切割成离散的静态画面；空间上，将连续画面切割成离散的网格。 解决连续动态的问题颇费周章，但处理一张表格就简单多了。所谓思路决定出路，大概就是这样吧。

 

　　眼前的障碍消除了，这事感觉可以做下去了。

　　动手之前，先做计划。完成这个任务，大致可分解成以下环节：

　　

1. 　　设定网格区域
2. 　　方块的生成
3. 　　方块的移动
4. 　　方块的旋转
5. 　　方块的消除
6. 　　GameOver的判断
7. 　　计分

 

 

　　One thing at a time. —— Mark Watney

 

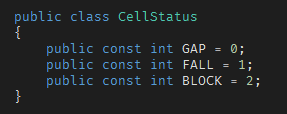
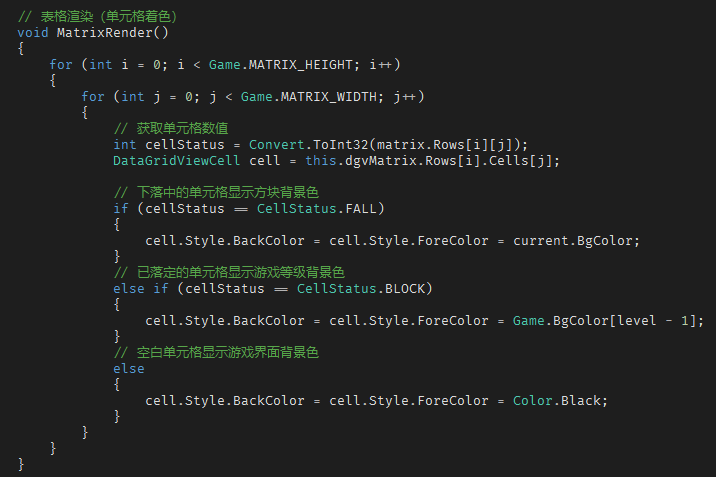
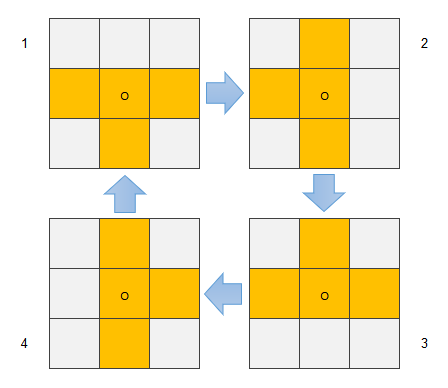
　　在开始之前，约定一下思路 —— 游戏界面由表格提供，表格内的单元格分为3种状态：

 

• 　　空白，值为0
• 　　下落中，值为1
• 　　已落定，值为2

　　对于下落中的方块，显示为方块本来的颜色；对于已落定的方块，显示为当前游戏级别对应的颜色（当年红白机上的版本就是这么设定的）。

　　所以，游戏画面的网格化抽象效果如下图所示：

    

　

　　参考代码：

　　状态常量设定  

　

 

　　表格渲染  

　

    

　　有了上面这样一个思路，下面就一步步实现具体的游戏逻辑。

 

　　首先，解决基础设施的问题——网格。

 

　　C#是少有的支持纯粹二维数组的语言，但说到表格，没有哪个对象比 DataTable 更方便了，尤其是配合 UI 组件 DataGridView。

　　我记得红白机上的俄罗斯方块，游戏的规格是宽10列，高25行（小时候数过，凡是小时候记过的事，好像就不会忘）。所以，最基础的设施就是一个包含 10 列, 25 行的DataTable. 之后所有的事情都围绕这个DataTable 来操作了。

 

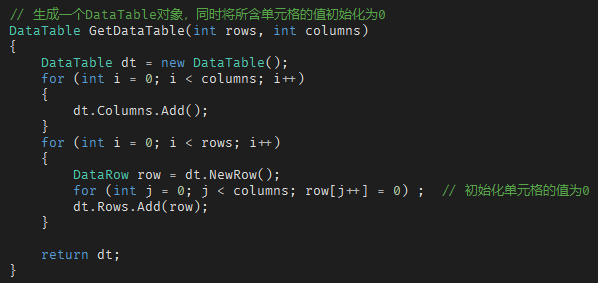
　　定义一个产生 DataTable，同时将内部单元格的值初始化为 0 的方法：

 

　

 

　　调用该方法产生一个 DataTable 变量，命名为 matrix，这就是整个游戏的基底：

 

　

 

　　其中，Game.MATRIX_HEIGHT 和 Game.MATRIX_WIDTH 是常量，分别为 25 和 20，代表着表格的尺寸。

 

　　现在，我们有了一个宽25列，高25行，内容全部都是数字 "0" 的表格了。

　　接下来是核心部件——方块。

    

　　方块的生成

 

　　游戏中需要不停地产生新的方块，每块一开始都会出现在顶部，这就需要有一个随机生成方法。

　　但在处理这个逻辑之前，首先要明确方块的构成。

　　前面提到，每个方块由 4 个方格组成。所以，可以通过一个包含 4 个元素的单元格数组来表示一个方块，每个单元格包含所在行列的位置索引，通过 4 组行列坐标可以确定一个方块在网格中的所占区域。额外的，每个方块有自己的颜色，相当于每个单元格数组中的元素拥有统一的背景色属性。

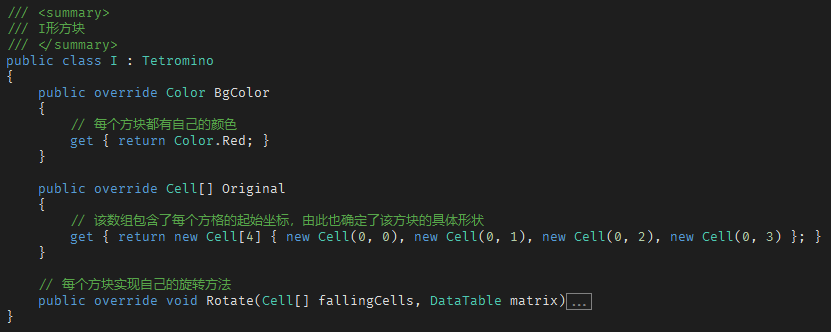
　　俄罗斯方块一共有 7 种，通常根据其形状，分别称作： I, J, L, S, Z, O, T. 

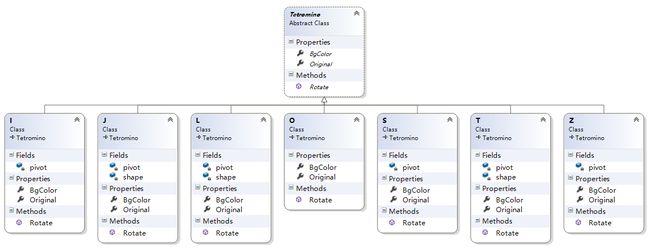
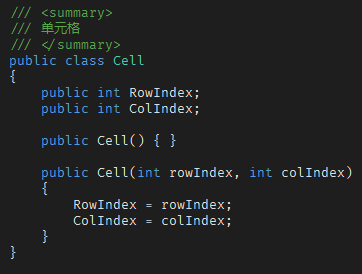
　　利用OOP的思想，我们可以先定义一个抽象类 Tetromino（Tetromino这个词的意思是“四连正方形”）。该抽象类包含 2 个只读的抽象属性：背景色、初始坐标，1个抽象方法：旋转。其中，初始坐标这个抽象属性定义为 Cell 类型的数组。Cell 是一个自定义类，包含 2 个 int 类型的属性，分别存储行、列索引。

 

　　类关系图如下：

 

    

　　Tetromino 定义如下：  

　

 

　　Cell 定义如下：

　

 

　　然后，分别定义 7 个具体形状的类，每个均继承Tetromino，并覆写其抽象成员。

    

　　以方块 " I " 为例：  

　

 

　　其它 6 种方块类的定义与此类似，略。

 

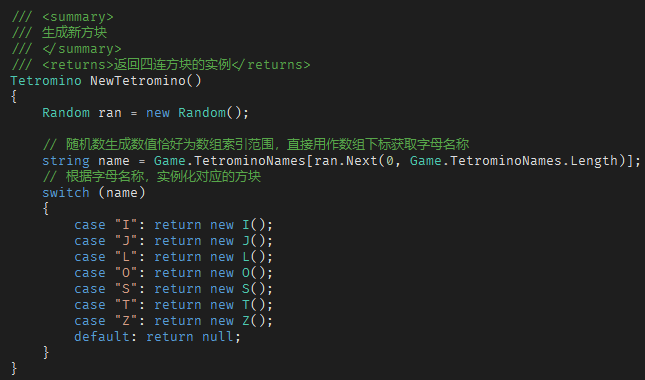
　　接下来，就是实现随机生成方块的方法了。很显然，需要用到随机数(Random)，可以这么来做：

　　定义一个静态字符串数组，内容就是7个字母 [ "I", "J", "L", "O", "S", "T", "Z" ]，然后设定 Random 的范围恰好就是 0~6 这七个正整数，对应数组的索引范围。每次随机生成一个数就等于指定了一个字母，最后，实例化该字母对应的方块类就可以了。

 

　　方块字母名称数组的定义：  

　

 

　　生成方法： 

　

 

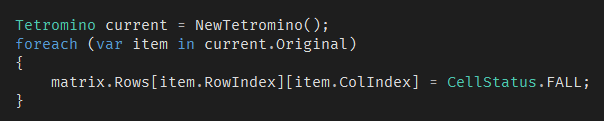
　　方块造出来之后，下一步就是显示在游戏界面中了。这里所谓的显示，指的是将方块初始位置对应的单元格修改为“下落“状态。

　　修改单元格的数值的实现方法如下：     

　

    

　　至此，方块的生成逻辑就处理完了。

 

　　方块的移动

 

　　移动总共有 3 个方向：左、右、下。这里暗含了一个判断逻辑——方块是否能够移动到目标位置，也就是前文中提到的“碰撞检测”的作用效果。

　　在表格化思维的基础上，所谓“碰撞检测”其实就是判断目标位置的单元格内是否已经有方块了，或者是否超出游戏界面的边界了。具体为：

 

• 　　判断单元格内是否有方块 = 判断单元格的数值是否等于表示有方块的状态值。
•        判断是否超出边界 = 判断单元格的坐标是否在表格的行、列范围内。

　　针对方块的移动操作，一定是作用于下落状态的方块。所以在执行动作之前，需要先获取当前正在下落中的方块的位置信息。根据前文的约定，处于下落状态的单元格的数值为 CellStatus.FALL， 通过这个约定，可以获取下落中的方块位置。

    

　

    

　　拿到了下落中方块的单元格位置信息，就可以操作向左、向右、向下移动了。

　　先来看向左移动的情况。

　　所谓向左移动，实现效果上相当于将 4 个下落中的单元格的列索引减1，行索引不变。其成立的前提条件是：左移之后的 4 个单元格的值均不为 CellStatus.BLOCK, 同时每个列索引大于等于 0.（因为向左移动是朝第 0 列的方向动）

　　当上面两个条件都满足时，就可以把方块向左平移 1 个单位列宽了。具体操作为：先将当前方块的单元格数值清零（CellStatus.GAP），然后把目标单元格的值设置为 CellStatus.FALL .

　　代码大概长这样：

　

 

　　右移的逻辑和左移是相似的，区别在于：

 

• 　　右移的具体实现是将单元格的列索引加1。
• 　　右移是朝表格的最大列索引方向移动，所以越界的判断标准是和最大列的列索引比较。

　　其余的逻辑是一致的，略。

 

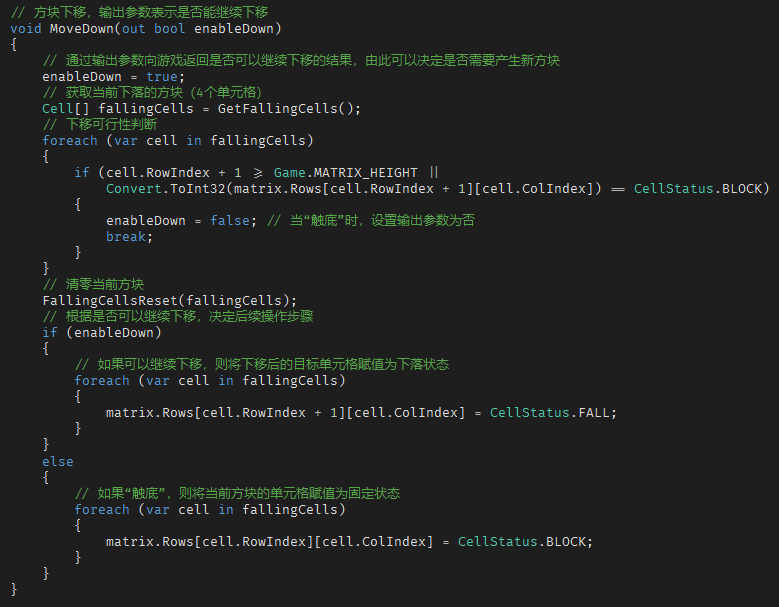
　　再来看方块的下移。

　　相较于左右移动，下移的操作是将下落方块的单元格的行索引加1，而列索引保持不变。“碰撞检测”的逻辑其实和左右移也类似，唯一的区别就是判断越界时，比较的是行索引。

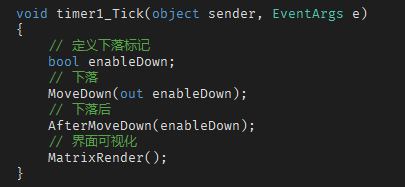
　　不过，相较于左右移动，下移操作含有附加逻辑：每当完成一次下移动作之后，需要立刻判断该方块是否“触底”？并由此决定是否将下落方块转换成固定方块，所谓“触底”，指的是已经到达游戏界面的底部或者是触及到了下方固定方块。一言蔽之，就是要判断该方块是否还能继续下移。一旦方块“触底”，则结束了该方块的下落周期了，需要将其转换成固定方块，并同时通知游戏产生新方块。

　　整个下移的代码差不多是这样的：

　

    

　　到这里，方块的移动就处理完了。

    

　　方块的旋转

 

　　旋转是游戏里的重头戏，俄罗斯方块之所以风靡全球，全靠这个 feature.

　　而这也是曾经让我感觉无从下手的地方，受限于鄙人愚钝的大脑，我完全没心情去推算图形旋转时的数学公式，虽然我觉得这里应该有一个三角函数上的解，或是其它什么数学上的玩意，可以一步搞定。（BTW，我数学不好全赖自己，和体育老师没有关系）

　　既然正面硬刚没把握，只好想别的办法从侧面绕过了。

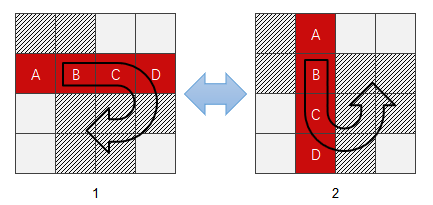
　　根据游戏规则，方块每次旋转为 90 度，在红白机上的操作好像是 A 键为顺时针转，B 键为逆时针转（这个不重要）。重点是，每个方块最多只有 4 种旋转形态。

　　更进一步的，对于 I 形、Z 形、S 型方块而言，因为形状本身具有对称性，所以这 3 个方块的旋转形态只有 2 种。事实上，在红白机的版本中，当按下旋转键时，这 3 个方块的旋转并不是一直朝一个方向旋转的，而是顺时针、逆时针交替进行，即只有两种形态变化。

　　再进一步，O 形方块不存在旋转变化，因为它就是一坨。

　　所以，真正会有 4 种旋转形态的是 L 形、J 形和 T 形，这 3 种方块。

　　也就是说，7 种方块总共包含：  3 * 4 + 3 * 2 + 0 = 18 (种) 旋转情形。那么，完全可以用穷举法，把 18 种情况逐个实现，就完整地解决了整个游戏的方块旋转问题了。

 

　　从变化多的下手。（ L 形，J 形，T 形），先说 T 形方块。

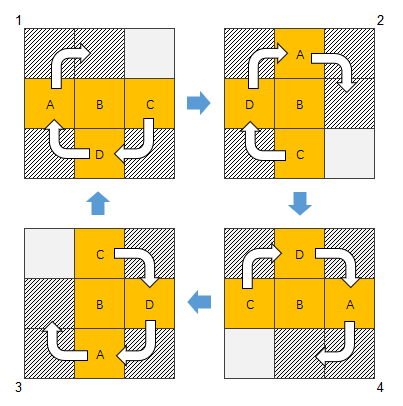
　　谈到旋转，自然要有一个轴心的概念，每个方块都存在一个旋转中心点。T 形方块的旋转点是就是横纵交叉的那个单元格。其 4 种旋转形态如下图所示：

　

　　如果将轴点单元格的行、列坐标表示为 [ x, y ]， 则 图1 中的方块坐标可以表示为 { [ x, y-1 ] , [ x, y ] , [ x, y+1 ] , [ x+1, y ] }.

　　4 种旋转过程可以演化成如下计算规则：

　　1 -> 2  : 将方块的坐标调整成 { [ x-1, y ], [ x, y-1 ], [ x, y ], [ x+1, y ] }.

　　2 -> 3 : 将方块的坐标调整成 { [ x-1, y ], [ x, y-1 ], [ x, y ], [ x, y+1 ] }.

　　3 -> 4 : 将方块的坐标调整成 { [ x-1, y ], [ x, y ], [ x, y+1 ], [ x+1, y ] }.

　　4 -> 1 : 将方块的坐标调整成 { [ x, y-1 ], [ x, y ], [ x, y+1 ], [ x+1, y ] }.

    

　　旋转逻辑就这么简单粗暴地搞定了。

　　且慢！这游戏里，任何动作都不能忘了“碰撞检测”。上面的方法只提供了如何旋转，但还缺一个判断能否旋转的逻辑。

　　和移动类似，旋转的可行性判断也包含目标单元格是否可用，这个不言自明。

　　额外的，为保证游戏效果更符合物理规律，还要包含一个每个单元格在其旋转路径中是否有阻挡的判断？

　　如图所示：

 

    

　

 

　　上图中的阴影区域，都属于旋转路径，不能有障碍物存在，否则，方块在物理上是转不动的。

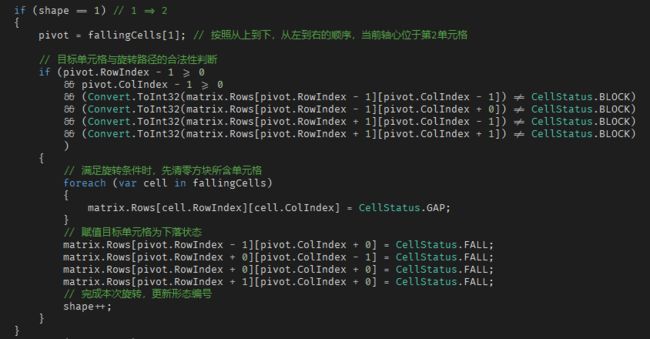
　　和分析旋转动作的方法类似，判断旋转可行性也是以轴心单元格为基础，通过相对位置逐个判断单元格是否合法。

　　代码实现如下，声明变量： 　　

　

 

　　1 => 2 ：  

　

 

　　以上代码为 T 形方块从形态 1 旋转到形态 2 的具体实现，其余 3 种旋转情况与此同理，代码从略。

 

　　至此，T 形方块的旋转方法就完结了。

　　L 形、J 形方块的做法和 T 形是一个道理，无非轴心格还有路径格的位置不同罢了，没有本质区别，故略。

 

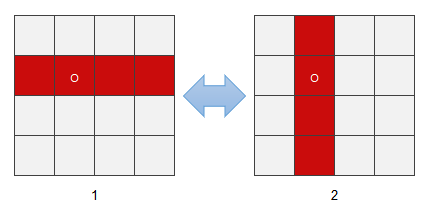
　　接下来看只有两种变化的方块( I 形、S 形、Z 形)，就以最受欢迎的 I 形方块为例。

　　I 形方块的轴心在第二块格子，也就是说它旋转起来是非对称的。其旋转时的单元格变化关系如下:

 

　

 

　　同样以轴心单元格为基础，设横、纵坐标为 [ x, y ] ，则它的旋转过程可量化成:

　　1 -> 2 : 将方块的坐标调整成 { [ x-1, y ], [ x, y ], [ x+1, y ], [ x+2, y ] }.

　　2 -> 1 : 将方块的坐标调整成 { [ x, y-1 ], [ x, y ], [ x, y+1 ], [ x, y+2 ] }.

    

　　I 形方块的旋转路径合法性检测如下:

    

　

    

　　严格来说，上面两幅图中的右下角单元格也应该纳入“碰撞检测”的范围内，但我故意去掉了对这个单元格的限制，因为这样可以提升游戏流畅度。

 

　　代码实现如下: 　　

　

 

　　Okay， I 形方块的旋转搞定了。

　　另外两个同类的 S 形、Z 形，实现原理一样，略。

 

　　现在还剩最后一个 O 形方块待处理，那就处理掉吧。

 

    　Talk is cheap, show me your code. -- Linus Torvalds

 

　　废话少说，直接上码：

 

　

 

　　O形方块，Over.

    

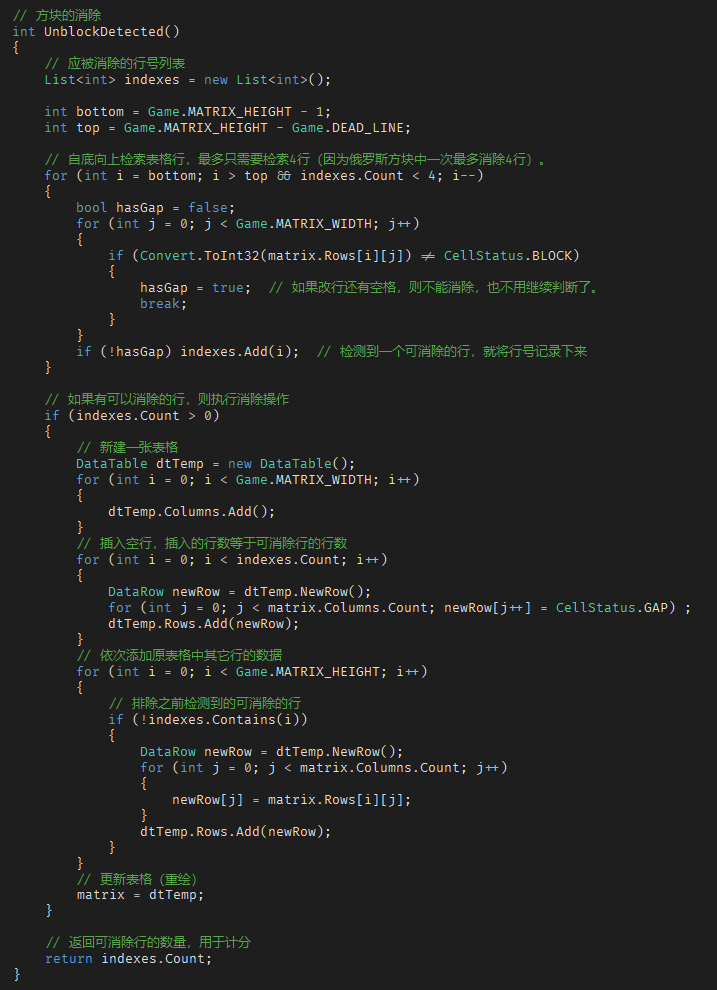
　　方块的消除

 

　　这可是续命的操作，得好好实现。

　　其实这一块的逻辑，相对来说是比较简单的。

　　从视觉上来看，当有一行或几行被消除了，则上方所有的方块就集体落下一行或几行，但落下过程并不会改变方块本身的相对位置。所以，可以将这一过程看成是：被消除的行，先变成空行，然后将该空行从当前位置抽出，并插入到表格的顶部，表格中原先的行自动往下顺移。如此就实现了方块的消除和下落补位的效果了。

　　主要代码实现大约长这样： 

　

    

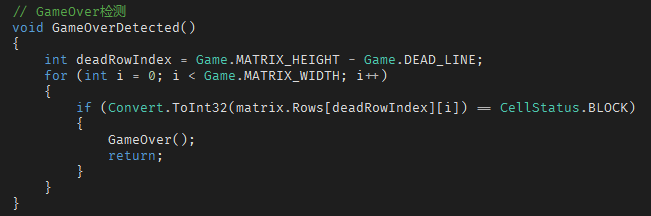
　　Game Over 的判断

 

　　虽然游戏界面的高度有 25 行，但根据红白机上的玩法来说，实际游戏空间的高度在 20 行，当落下任意一个方块，其高度达到第21行时，就GG了。

　　根据这个规则，判断游戏结束的标准也就是判断第 21 行是否有固定方块了（这里描述时是从底往上数，实际代码实现时是从顶往下数）。

　　代码如下图所示：  

　

 

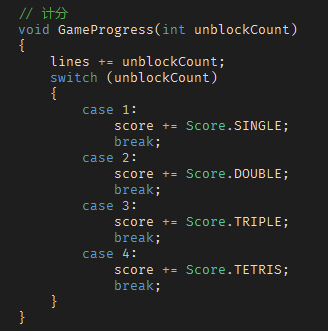
　　计分

 

　　分数其实不是游戏的必须，前文已经介绍的部分，已经可以组装起一个可玩的游戏了。但是，如果俄罗斯方块没有分数的话，那就像赌博不带彩，瞬间没有存在价值了。所以，分数其实又是游戏的必须。我和老爸就曾为了争个最高分数，斗到老妈发飙“你们俩再不来吃饭我把菜都倒垃圾桶！”

 

　　按照红白机上的玩法，俄罗斯方块的计分规则分为 3 项：

 

• 　　得分
• 　　消除行数
• 　　等级

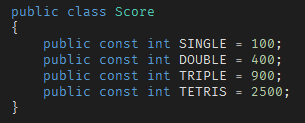
　　一次消除一行，得100分

　　一次消除两行，得400分

　　一次消除三行，得900分

　　一次消除四行，得2500分

 

　　每次发生消除时，得分和消除行数累加。

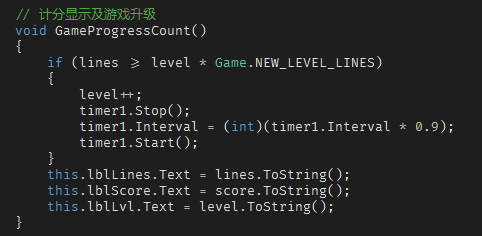
　　每累计消除 30 行，游戏等级增加 1 级。 

　　等级越高，方块下落速度越快，至于到底提速多少，我也搞不清楚。在我自己做的这个版本里，我设定为增速10%.

 

　　部分代码：

　　

　

 

　　其中，分数值做成了常量：

    

　

 

　　游戏等级升级及分数显示：

 

　

 

　　至此，游戏中所有的业务逻辑都已被实现，最后就剩把这些业务逻辑按照游戏的玩法组合起来了。

　　首先，当游戏开始前，大约需要做以下事情：

 

1. 　　生成游戏界面表格
2. 　　生成预览表格（根据红白机的玩法，游戏过程应该包含提示下一个方块的预览功能）
3. 　　准备一个定时器
4. 　　启动游戏

　　代码参考：

    

　   

 

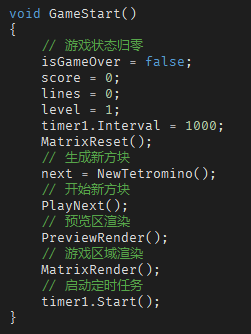
　　在启动游戏阶段，大约需要做以下事情：

 

1. 　　计数清零
2. 　　生成新方块
3. 　　生成下一个方块
4. 　　界面重绘
5. 　　启动定时任务

　　代码参考：

    

　

    

　　定时任务中包含了方块的下落操作。而在方块完成一次下落之后，需要判断方块是否可以继续下落？

　　　　如果方块可以继续下落，则继续；

　　　　如果已经触底了，则需要对游戏界面的状态进行更新，紧接着判断游戏是否结束？

　　　　　　如果游戏结束，则结束当前游戏；

　　　　　　如果游戏未结束，则进行计分操作并开始新的方块；

 

　　代码参考：

 

　　定时任务

    

　

   

　　下落后处理

    

　

 

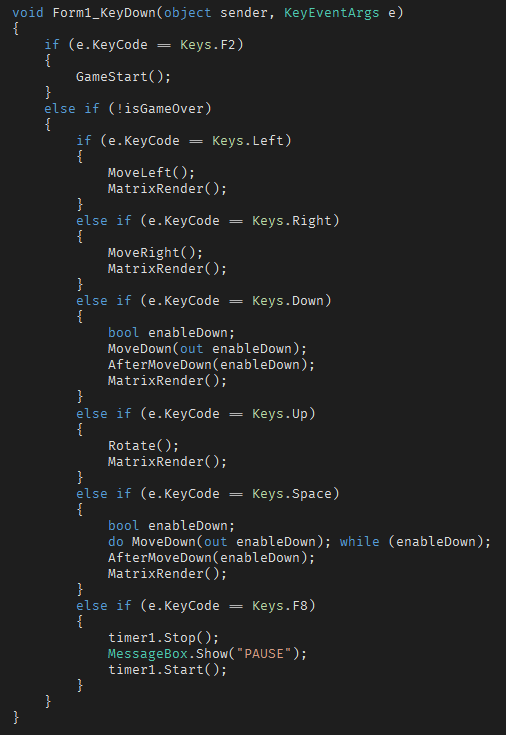
　　而在方块下落的过程中，需要监听键盘事件，完成相应的事件处理：

 

• 　　上：执行旋转
• 　　下：方块向下移动一行
• 　　左：方块向左移动一列
• 　　右：方块向右移动一列
• 　　空格：方块快速下落（直接一落到底）
• 　　F2： 重新开始
• 　　F8： 暂停

　　代码参考：

 

　

 

　　That's all .

 

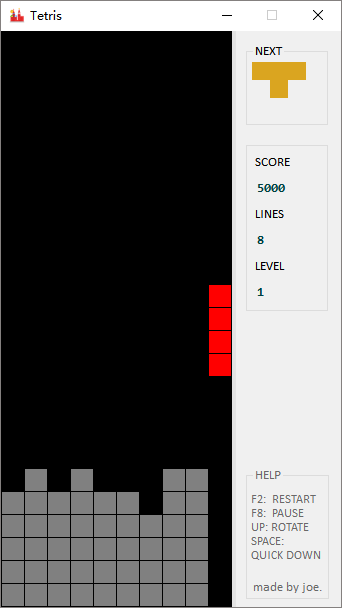
　　到此，所有的事情都做完了，该玩一把了。

 

　

 

 

　　Bug Report

    

　　在我以前的一篇文章里，我说过 " No bug, no code. "，我再补充一句：“没有例外。”

 

　　游戏能玩，但有两处遗憾：

　　1.  当平移或者旋转方块时，会中断方块的自动下落过程。而在红白机上方块会持续下落。

　　2.  根据我设计的旋转逻辑，当I形方块贴着游戏界面的边框时，无法旋转，因为旋转路径检测会不通过。但是在红白机上的，同样的情况，可以旋转，其产生的效果有点像方块在边框上打滑了一下然后被挤开。

　　虽然明知存在瑕疵，但在我一气呵成写完整份代码后，已无心修复。

　　毕竟能玩了，毕竟，我又不是处女座。

　　

 

　　写在最后

 

　　听说俄罗斯方块是游戏开发领域的 " hello world "，这么说来，我也算入门游戏设计了？呵呵~

　　决定写这个程序是在一个周末的午后，动手前估计着周末两天应该都得搭进去了。但当我完成核心代码并玩上第一把的时候，天还没黑，差不多用了也就一个下午的工夫，精确点说，大约 4 个小时左右。说实在的，我自己都很意外。如果我参加一个面试，要求在 4 个小时的时间内做一个俄罗斯方块，我肯定直接 “谢谢，再见” 了。不禁回想当年初学 C# 时，就想做这个游戏，却浅尝辄止，竟搁置了这么久才实现，惭愧。讽刺的是，如今我写下的这份代码，完全基于 .NET 2.0 的框架，C# 2.0 的语法，完全没有超出当年我初学 C# 时的知识体系。

    

　　反思之余，就用一句我很喜欢的英语格言作为结束吧：

 

　　WHEN THE GOING GETS TOUGH ,  THE TOUGH GET GOING .

 

 

 

　　附 

　　完整代码(GitHub地址)： https://github.com/sherrywasp/tetris.git