---恢复内容开始---
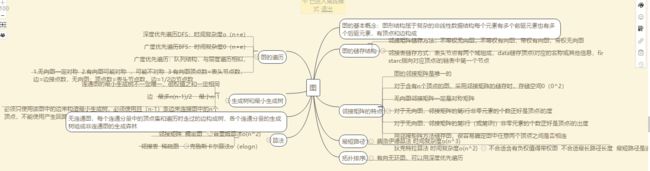
1、思维导图
2、图的学习体会
(1)首先理解图的定义,有顶点和边组成,所有的定点的度之和等于边数的两倍,完全无向图的边为n(n-1)/2;完全有向图n(n-1);图还分为稠密图和疏密图;
强连通图有n个顶点,n条边,最多有n(n-1)条边。无向图n个顶点至少n条边。
(2)邻接矩阵:无向图,一定对称。有向图,可能对称,可能不对称。图的邻接矩阵表示是唯一的。对于含有n个顶点的图,采用邻接矩阵存储,比较适合稠密图
(3)无向图的邻接矩阵一定是一个对称矩阵。
(4)用邻接矩阵方法储存图,很容易确定图中任意两个顶点之间是否有边相连。
(5)邻接表表示不唯一
(6)DFS深度优先遍历,BFS广度优先遍历用队列结构。
(7)一个连通图的最小生成树不一定唯一,权值之和一定相同。
(8)有向无环,还可用深度优先遍历算法,邻接表。AOE网带权的有向无环图。
但是编译、运行代码的有点困难,理解起来太困难,学了之后有点混乱,不过我会努力去理解,多多练习。
2 、PTA实验练习
题目一
2.1图着色问题
1·设计思路
先建立一个无向图,包括顶点,边,颜色数的定义名称,然后顶点和颜色都从1到V编号。
随后E行,每行给出一条边的两个端点的编号。
把图建好后int一个正整数n,代表待检查的颜色分配方案的个数。
随后N行,每行顺次给出V个顶点的颜色(第i个数字表示第i个顶点的颜色)
无向图是合法的(不存在自回路和重边)
建一张图存储关系,查集求出是朋友的人,然后在图中将并查集中的点都连边,最后判断边的权值
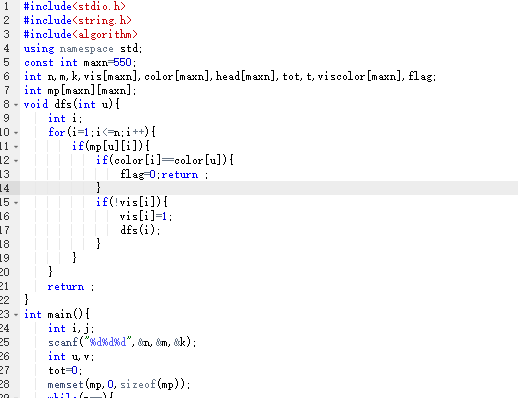
2·伪代码
int i,j;
scanf("%d%d%d",&n,&m,&k);
int u,v;
tot=0;
memset(mp,0,sizeof(mp));
while(m--){
scanf("%d%d",&u,&v);
mp[u][v]=mp[v][u]=1;
}
scanf("%d",&t);
while(t--){
int sum=0;
flag=1;
memset(viscolor,0,sizeof(viscolor));
for(i=1;i<=n;i++){
scanf("%d",&color[i]);
if(!viscolor[color[i]]){
sum++;
viscolor[color[i]]=1;
}
}
if(sum!=k){
printf("No\n");
continue;
}
memset(vis,0,sizeof(vis));
for(i=1;i<=n;i++){
if(!vis[i]){
if(!flag)
break;
vis[i]=0;
dfs(i);
}
}
如果flag=1;
输出No;
else
输出Yes
}
3·代码截图
4·PTA提交说明
题目二
2.2排座位
1、设计思路
输入第一行给出3个正整数:N(前来参宴的宾客总人数)则这些人从1到N编号;M为已知两两宾客之间的关系数;K为查询的条数。随后M行,每行给出一对宾客之间的关系,格式为:宾客1 宾客2 关系,其中关系为1表示是朋友,-1表示是死对头。注意两个人不可能既是朋友又是敌人。最后K行,每行给出一对需要查询的宾客编号
2、伪代码
先输入fa[MAX];
int 函数Find(int a)
{
如果 fa[a]等于a
返回 a;
否则 返回 Find(fa[a]);
}
void 函数Union(int a,int b)
{
int faa=Find(a)赋值;
int fab=Find(b);
if(faa==fab)
return ;
fa[faa]=fab;
}
int main()
{
打开文件stout和stdin
int N,M,K;
while(scanf("%d%d%d",&N,&M,&K)!=0)
{
memset(g,0x3f,sizeof(g));
for(int i=1;i<=N;i++)
fa[i]=i;
while(M--)
{
int a,b,r;
scanf("%d%d%d",&a,&b,&r);
if(r==1)
{
g[a][b]=g[b][a]=1;
Union(a,b);
}
else if(r==-1)
{
g[a][b]=g[b][a]=-1;
}
}
for(int i=1;i<=N;i++)
{
Set[i].clear();
for(int j=1;j<=N;j++)
{
if(Find(j)==i) Set[i].push_back(j);
}
}
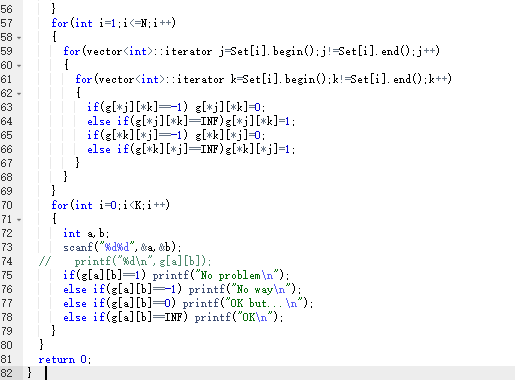
for(int i=1;i<=N;i++)
{
for(vector
{
for(vector
{
如果g[*j][*k]等于-1
g[*j][*k]等于0;
else if(g[*j][*k]==INF)
g[*j][*k]等于1;
如果g[*k][*j]等于-1
g[*k][*j]等于0;
else if(g[*k][*j]==INF)g[*k][*j]=1;
}
}
}
for(int i=0;i
int a,b;
输入("%d%d",&a,&b);
如果g[a][b]等于1
输出No problem;
else if(g[a][b]==-1) 输出No way;
else if(g[a][b]==0) 输出OK but...;
else if(g[a][b]==INF) 输出"OK;
}
}
3、代码截图
4、PTA提交说明
题目三
2·3公路村村通
1、设计思路
prim算法求最小生成树,从 1 开始;
2、伪代码
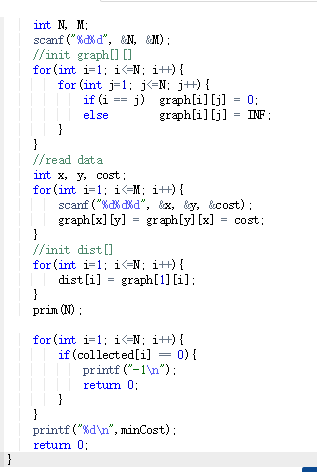
void prim(const int N){
collected[1] = 1; //以1号结点作为开始
while (ture) {
定义minPos,MinDist;
minPos 返回-1;
MinDist返回INF;
for(int i=1; i<=N; i++){
if(collected[i]==0 && dist[i]
minDist 等于dist[i];
}
}
如果minPos 等于 -1
用break结束;
collected[minPos] 等于 1;
minCost 等于 minCost+dist[minPos];
for(int i=1; i<=N; i++){
如果collected[i]恒等于0 并且 graph[minPos][i]小于dist[i]{
dist[i] 等于 graph[minPos][i];
}
}
}
3、代码截图
4、PTA提交说明
三、截图本周题目集的PTA最后排名
四、阅读代码
#include
#include
#include
using namespace std;
int v, e, k;
int map[501][501] = {0};
int color[501] = {0};
bool flag = true;
bool vis[501];
void isYes(int i)
{ if (vis[i] || flag == false)
{ return; }
vis[i] = true;
for (int j = 0; j < v;j++)
{ if (color[i] == color[j] && map[i][j] == 1)
{ flag = false; return; }
else if (map[i][j] == 1 && vis[j] == false
){ isYes(j); } } }
int main()
{ cin >> v >> e >> k;
for (int i = 0; i < e; i++)
{ int x, y; cin >> x >> y; x--;
y--; map[x][y] = 1;
map[y][x] = 1; }
int m; cin >> m;
for (int i = 0; i < m; i++)
{ set<int> s;
for (int j = 0; j < v; j++)
{ int c; cin >> c; s.insert(c);
color[j] = c; }
if (s.size() != k)
{ flag = false; }
else { memset(vis, false, sizeof(vis));
flag = true; for (int j = 0; j < v; j++)
{ isYes(j); if (flag == false) { break; } } }
if (flag) { cout << "Yes" << endl; }
else { cout << "No" << endl; } }
return 0; }
这个代码是从网上搜的,比我的代码简短,直接用图的遍历,遍历的时候判断是否颜色相等即可。
注意需要不同颜色的个数需要等于k
---恢复内容结束---