C程序编写的FFT与matlab中的fft函数比较

C程序编写的FFT与matlab中的fft函数比较

一、FFT的C程序编写

在我的上一篇博客已经讲过如何用C语言编写一个FFT变换，不清楚的可以打开下面这个链接阅读

FFT详解

经过对原来程序的修改，现在可以实现一下功能：

1、可以对一个连续的时域信号进行采样，将其转换为离散的时域信号。

2、可以输入输入采样点数目和采样频率来进行FFT变换。

3、可以将FFT变换结果通过gnuplot画出来。

程序如下：

#include
#include
#include
#define N 1024 
typedef struct{
	double real;
	double imag;
}complex;
complex x[N], *W;
int size=0;
double l[5000],h[5000];
double PI=4.0*atan(1);
void output()
{
	int i;
	for(i=0;i<size;i++)
	{	
		printf("%lf  %lf  %.4f",h[i],l[i],x[i].real);//输出频域序列 模长 和信号的实部
		if(x[i].imag>=0.0001)
		{
			printf("+%.4fj\n",x[i].imag);
		}
		else if(fabs(x[i].imag)<0.0001)
		{
			printf("\n");
		}
		else
		{
			printf("%.4fj\n",x[i].imag);
		}
	}
}
void change()
{
	complex temp;
	unsigned short i=0,j=0,k=0;
	double t;
	for(i=0;i<size;i++)
	{
		k=i;
		j=0;
		t=(log(size)/log(2));
		while( (t--)>0 )
		{
			j=j<<1;
			j|=(k & 1);
			k=k>>1;
		}
		if(j>i)
		{
			temp=x[i];
			x[i]=x[j];
			x[j]=temp;
		}
	}
}
void transform()
{
	int i;
	W=(complex *)malloc(sizeof(complex) * size);
	for(i=0;i<size;i++)
	{
		W[i].real=cos(2*PI/size*i);
		W[i].imag=-1*sin(2*PI/size*i);
	}
}
void add(complex a,complex b,complex *c)
{
	c->real=a.real+b.real;
	c->imag=a.imag+b.imag;
}
void sub(complex a,complex b,complex *c)
{
	c->real=a.real-b.real;
	c->imag=a.imag-b.imag;
}
void mul(complex a,complex b,complex *c)
{
	c->real=a.real*b.real - a.imag*b.imag;
	c->imag=a.real*b.imag + a.imag*b.real;
}
void fft()
{
	int i=0,j=0,k=0,m=0;
	complex q,y,z;
	change();
	for(i=0;i<log(size)/log(2) ;i++)
	{
		m=1<<i;
		for(j=0;j<size;j+=2*m)
		{
			for(k=0;k<m;k++)
			{
				mul(x[k+j+m],W[size*k/2/m],&q);
				add(x[j+k],q,&y);
				sub(x[j+k],q,&z);
				x[j+k]=y;
				x[j+k+m]=z;
			}
		}
	}
}
int main()
{
	int i;
	double fs;
	double t[5000];
	printf("输入采样个数和采样频率\n");
	scanf("%d %lf",&size,&fs);//输入的采样点数和采样频率
	for(i=0;i<size;i++)
	{
		t[i]=i/fs;  //时间序列
		x[i].real=0.5*sin(2*PI*25*t[i]);//输入连续时间信号，并对其进行采样
		x[i].imag=0;
		h[i]=i*(fs/(double)size);//频率序列
	}
	transform();
	fft();
	for(i=0;i<size;i++)  //计算变换结果的模长
	{
		l[i]=sqrt(x[i].imag*x[i].imag+x[i].real*x[i].real) ;
	}
	printf("输出FFT后的结果\n");
	output();
	return 0;
}

二、输出结果演示

从程序中可以看出输入的信号为0.5sin(2PI25t)

程序运行演示如下：

输入采样点数为512 采样频率为100。

第一行对应的是频率，

第二行对应的是变换结果的模长。

第三行对应的是每个采样点的变换结果。

三、使用gnuplot画出函数图像

plot [0:100] [0:150] "F6.dat" u 1:2 w l

画图结果：

横坐标为频率，纵坐标为模值

四、与matlab中的fft函数进行比较

>> fs=100;
>> N=512;
>> n=0:N-1;
>> t=n/fs;
>> y=0.5*sin(2*pi*25*t);
>> x=fft(y,N);
>> m=abs(x);
>> f=n*fs/N;
>> plot(f,m);
>> xlabel('频率/Hz');
>> ylabel('振幅');title('N=512');
>> grid on;

输出结果为

结论：用C语言编写的FFT程序输出效果跟matlab基本一致。

总结：通过这几天对FFT的学习，基本了解了它的算法原理，对它的输入和输出也有了深刻的了解，但是这次的C程序还有一些不足之处，就是当采样点没有达到2的整数次幂的时候没有自动补零的功能。

后续

经过对程序改进，现在可以实现自动补0.

#include
#include
#include
#define N 1024
typedef struct{
	double real;
	double imag;
}complex;
complex x[N], *W;
int size=0;
double l[5000],h[5000];
double PI;
double fs;
int FN;
void output()
{
	int i;
	for(i=0;i<FN;i++)
	{	
		printf("%lf  %lf  %.4f",h[i],l[i],x[i].real);
		if(x[i].imag>=0.0001)
		{
			printf("+%.4fj\n",x[i].imag);
		}
		else if(fabs(x[i].imag)<0.0001)
		{
			printf("\n");
		}
		else
		{
			printf("%.4fj\n",x[i].imag);
		}
	}
}
void change()
{
	complex temp;
	unsigned short i=0,j=0,k=0;
	double t;
	for(i=0;i<FN;i++)
	{
		k=i;
		j=0;
		t=(log(FN)/log(2));
		while( (t--)>0 )
		{
			j=j<<1;
			j|=(k & 1);
			k=k>>1;
		}
		if(j>i)
		{
			temp=x[i];
			x[i]=x[j];
			x[j]=temp;
		}
	}
	//output();
}
void transform()
{
	int i;
	W=(complex *)malloc(sizeof(complex) * FN);
	for(i=0;i<FN;i++)
	{
		W[i].real=cos(2*PI/FN*i);
		W[i].imag=-1*sin(2*PI/FN*i);
	}
}
void add(complex a,complex b,complex *c)
{
	c->real=a.real+b.real;
	c->imag=a.imag+b.imag;
}
void sub(complex a,complex b,complex *c)
{
	c->real=a.real-b.real;
	c->imag=a.imag-b.imag;
}
void mul(complex a,complex b,complex *c)
{
	c->real=a.real*b.real - a.imag*b.imag;
	c->imag=a.real*b.imag + a.imag*b.real;
}
void fft()
{
	int i=0,j=0,k=0,m=0;
	complex q,y,z;
	change();
	for(i=0;i<log(FN)/log(2) ;i++)
	{
		m=1<<i;
		for(j=0;j<FN;j+=2*m)
		{
			for(k=0;k<m;k++)
			{
				mul(x[k+j+m],W[FN*k/2/m],&q);
				add(x[j+k],q,&y);
				sub(x[j+k],q,&z);
				x[j+k]=y;
				x[j+k+m]=z;
			}
		}
	}
}
int main()
{
	int i;
	PI=4.0*atan(1);
	double t[5000];
	printf("输入数据个数\n");
	scanf("%d %d %lf",&size,&FN,&fs);
	for(i=0;i<size;i++)
	{
		t[i]=i/fs;
		x[i].real=0.5*sin(2*PI*25*t[i]);
		x[i].imag=0;
	}
	transform();
	fft();
	for(i=0;i<FN;i++)
	{
		l[i]=sqrt(x[i].imag*x[i].imag+x[i].real*x[i].real) ;
		h[i]=i*(fs/(double)FN);
	}
	printf("输出FFT后的结果\n");
	output();
	return 0;
}

在命令窗口中输入指令：

plot [0:100] [0:15] "ff66.dat" u 1:2 w l

运行结果：

数据点为50，采样点为128，采样频率为100

matlab实现:

>> N=50;
>> NFFT=128;
>> fs=100;
>> n=0:N-1;
>> t=n/fs;
>> y=0.5*sin(2*pi*25*t);
>> x=fft(y,NFFT);
>> m=abs(x);
>> f=(0:NFFT-1)*fs/NFFT;
>> plot(f,m);
>> xlabel('频率/Hz');ylabel('振幅');
>> title('N=50 NFFT=128');grid on;

输出结果：

增大采样点数和数据点数，

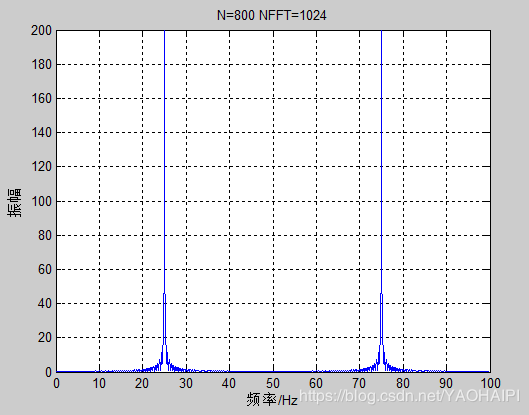
现在把数据点设为800，采样点设为1024。

运行结果：

matlab实现

>> N=800;
>> NFFT=1024;
>> n=0:N-1;
>> fs=100;
>> t=n/fs;
>> y=0.5*sin(2*pi*25*t);
>> x=fft(y,NFFT);
>> m=abs(x);
>> f=(0:NFFT-1)*fs/NFFT;
>> plot(f,m);
>> xlabel('频率/Hz');ylabel('振幅');
>> title('N=800 NFFT=1024');grid on;

运行结果：

结论：用C语言基本实现了matlab中fft函数的作用。