OpenGL ES 2.0 (iOS)[02]：修复三角形的显示

---

目录

一、分析拉伸的原因

1、修复前后照片对比
2、从问题到目标，分析原因

二、准备知识，三维变换

1、4 x 4 方阵
2、线性变换（缩放与旋转）
3、平移
4、向量（四元数）
5、w 与 其它

三、OpenGL 下的三维变换

1、OpenGL 的坐标系
2、OpenGL 的 gl_Position 是行向量还是列向量
3、单次三维变换与多次三维变换问题
4、OpenGL 的变换是在那个阶段发生的，如何发生

四、修复拉伸问题

1、改写 Shader Code
2、应用 3D 变换知识，重新绑定数据
  1) 在 glLinkProgram 函数之后，利用 glGetUniformLocation 函数
     得到 uniform 变量的 location (内存标识符)
  2) 从 Render Buffer 得到屏幕的像素比（宽：高）值，即为缩小的值
  3) 使用 Shader Program , 调用 glUseProgram 函数
  4) 使用 3D 变换知识，得到一个缩放矩阵变量 scaleMat4
  5) 使用 glUniform* 函数把 scaleMat4 赋值给 uniform 变量
3、完整工程

---

一、分析拉伸的原因

1、修复前后照片对比

问题与目标

图片通过 sketch 制作

2、从问题到目标，分析原因

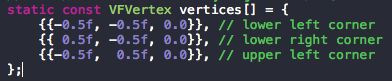
1、它们的顶点数据均为：

顶点数组

VFVertex

2、借助 Matlab 把顶点数据绘制出来：

分布图

从图可以看出，这三个数据形成的其实是一个等边直角三角形，而在 iOS 模拟器中通过 OpenGL ES 绘制出来的是直角三角形，所以是有问题的，三角形被拉伸了。

3、on-Screen （屏幕） 的像素分布情况：

1. iPhone6s Plus 屏幕：5.5寸，1920 x 1080 像素分辨率，明显宽高比不是 1:1 的;

2. OpenGL ES 的屏幕坐标系 与 物理屏幕的坐标系对比：

   
   
   

   OpenGL ES 的屏幕坐标系
   
   
   

   物理屏幕的坐标系

分析：前者是正方体，后者长方体，不拉伸才怪。

3. 首先，OpenGL 最后生成的都是像素信息，再显示在物理屏幕上；通过 1) 和 2) 可以知道 Y 方向的像素数量大于 X 方向的像素数量，导致真实屏幕所生成的 Y 轴与 X 轴的刻度不一致（就是Y=0.5 > X=0.5），从而引起了最后渲染绘制出来的图形是向 Y 方向拉伸了的。

动画演示修复:

FixTriangle.gif

所以要做的事情是，把顶点坐标的 Y 坐标变小，而且是要根据当前显示屏幕的像素比来进行缩小。

Gif 图片，由 C4D 制作，PS 最终导出；

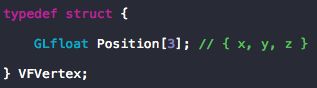
4. 在 Shader 里面，v_Position 的数据类型是 vec4 ，即为4分量的向量数据{x,y,z,w};就是说，要把这个向量通过数学运算变成适应当前屏幕的向量。

---

二、准备知识，三维变换

-- 建议 --：如果向量、矩阵知识不熟悉的可以看看《线性代数》一书；如果已经有相应的基础了，可以直接看《3D数学基础：图形与游戏开发》，了解 3D 的世界是如何用向量和矩阵知识描述的；若对 3D 知识有一定的认识，可以直接看《OpenGL Programming Guide》8th 的变换知识, 或 《OpenGL Superblble》7th 的矩阵与变换知识，明确 OpenGL 是如何应用这些知识进行图形渲染的。

注：以下核心知识均来源于，《3D数学基础：图形与游戏开发》，建议看一下第8章；

4x4 整体

图片通过 sketch 制作，请放大看

1、4 x 4 方阵

4X4方阵

• 1. 它其实就是一个齐次矩阵，是对3D运算的一种简便记法；
• 2. 3x3矩阵并没有包含平移，所以扩展到4x4矩阵，从而可以引入平移的运算；

2、线性变换（缩放与旋转）

线性变换

• n，是标准化向量，而向量标准化就是指单位化：
  
  

  normalied

a、 v不能是零向量，即零向量为{0，0，0}；
b、||v||是向量的模，即向量的长度；
c、例子是2D向量的，3D/4D向量都是一样的
【 sqrt(pow(x,2)+pow(y,2)+pow(w,2)...) 】

图片来源于《3D数学基础：图形与游戏开发》5.7

• k，是一个常数；

• a，是一个弧度角；

1) 线性缩放

线性缩放

• XYZ 方向的缩放：

  
  
  

X方向，就是{1，0，0}；Y方向，就是{0，1，0}；Z方向，就是{0，0，1}；分别代入上面的公式即可得到。

图片来源于《3D数学基础：图形与游戏开发》8.3.1

2) 线性旋转

线性旋转

• X方向{1，0，0}的旋转：

  
  
  

• Y方向{0，1，0}的旋转：

  
  
  

• Z方向{0，0，1}的旋转：

  
  
  

图片来源于《3D数学基础：图形与游戏开发》8.2.2

3、平移

平移

直接把平移向量，按分量{x, y, z}依次代入齐次矩阵即可；

图片来源于《3D数学基础：图形与游戏开发》9.4.2

4、向量（四元数）

四元数

a.向量，即4D向量，也称齐次坐标{x, y, z, w}; 4D->3D，{x/w, y/w, z/w}；

b.四元数，[ w, v ]或[ w, (x,y,z) ]两种记法，其中 w 就是一个标量，即一个实数；

c.点乘

矩阵乘法，点乘

c.1 上面两种是合法的，而下面两种是不合法的，就是没有意义的；
c.2 第一个为 A(1x3) 行向量(矩阵)与 B(3x3)方阵的点乘，第二个是 A(3x3) 的方阵与 A(3x1) 的列向量(矩阵)的点乘；

图片来源于《3D数学基础：图形与游戏开发》7.1.7

5、w 与 其它

这块内容现在先不深究，不影响对本文内容的理解。

• W
  
  

  w

w，与平移向量{x, y, z}组成齐次坐标；一般情况下，都是1；

• 投影
  
  

  投影

这里主要是控制投影，如透视投影；如：

图片来源于《3D数学基础：图形与游戏开发》9.4.6

---

三、OpenGL 下的三维变换

这里主要讨论第一阶段 Vertex 的 3D 变换，对于视图变换、投影变换，不作过多讨论；如果要完全掌握后面两个变换，还需要掌握 OpenGL 下的多坐标系系统，以及摄像机系统的相关知识。

1、OpenGL 的坐标系

• 坐标系方向定义分两种：

  
  
  

图片来源于，《3D数学基础：图形与游戏开发》8.1；左右手坐标系是用来定义方向的。

• 旋转的正方向

  
  
  

  右手坐标

图片来源于，Diney Bomfim 的《Cameras on OpenGL ES 2.x - The ModelViewProjection Matrix》；这个就是 OpenGL 使用的坐标系，右手坐标系；其中白色小手演示了在各轴上旋转的正方向（黑色箭头所绕方向）；

2、OpenGL 的 gl_Position 是行向量还是列向量

• 这里讨论的核心是，gl_Position 接收的是 行向量，还是列向量？

行向量

列向量

• 讨论行列向量的目的是明确，3D 矩阵变换在做乘法的时候是使用左乘还是右乘；

图片来源于，《线性代数》矩阵及其运算一节

从图中的结果就可以看出，左乘和右乘运算后是完全不一样的结果；虽然图片中的矩阵是 2 x 2 方阵，但是扩展到 n x n 也是一样的结果；

• 那么 OpenGL 使用的是什么向量？

图1，列向量

• 英文大意：矩阵和矩阵乘法在处理坐标系显示模型方面是一个非常有用的途径，而且对于处理线性变换而言也是非常方便的机制。

图2

红框处的向量就是 v_Position 顶点数据；即 OpenGL 用的是列向量；（木有找到更有力的证据，只能这样了）

• 左乘右乘问题？

图3

• 英文大意：在我们的视图模型中，我们想通过一个向量来与矩阵变换进行乘法运算，这里描述了一个矩阵乘法，向量先乘以 A 矩阵再乘以 B 矩阵：

很明显，例子使用的就是左乘，即 OpenGL 用的是左乘；

图 1、3 来源于，《OpenGL Programming Guide 8th》第5章第二节
图 2 来源于，《3D数学基础：图形与游戏开发》7.1.8

3、单次三维变换与多次三维变换问题

多次变换

1. OpenGL 的三维变换整体图：

4x4 整体 OpenGL

因为列向量的影响，在做点乘的时候，平移放在下方与右侧是完全不一样的结果，所以进行了适应性修改

• 平移部分的内容：

4X4方阵 OpenGL

平移 OpenGL

• 矩阵平移公式

等式左侧：A(4x4)方阵点乘{v.x, v.y, v.z, 1.0}是顶点数据列向量；右侧就是一个 xyz 均增加一定偏移的列向量

图片来源于，《OpenGL Superblble》7th, Part 1, Chapter 4. Math for 3D Graphics

• 投影（就是零）

投影 OpenGL

2. 所有的变换图例演示

物体的坐标是否与屏幕坐标原点重叠

Linaer Transforms

• 单次变换（原点重叠）

Identity

无变换，即此矩阵与任一向量相乘，不改变向量的所有分量值，能做到这种效果的就是单位矩阵，而我们使用的向量是齐次坐标{x, y, z, w}，所以使用 4 x 4 方阵；{w === 1}.

• 缩放

Scale

单一的线性变换——缩放，缩放变换是作用在蓝色区域的 R(3x3) 方阵的正对角线（从m11(x)->m22(y)->m33(z)）中;例子是 X、Y、Z 均放大 3 倍。

• 旋转

Rotate

单一的线性变换——旋转，旋转变换是作用在蓝色区域的 R(3x3) 方阵中;例子是绕 Z 轴旋转 50 度。

• 平移

Translation

单一的线性变换——平移，平移变换是作用在绿色区域的 R(3x1) 矩阵中（{m11, m21, m31}对应{x, y, z}）;例子是沿 X 正方向平移 2.5 个单位。

• 单次变换（原点不重叠）

Translation&Scale

Translation&Rotate

以上图片内容来源于《OpenGL Programming Guide》8th, Linear Transformations and Matrices 一小节，使用 skecth 重新排版并导出

3. 多次变换

连续变换

这里的问题就是先旋转还是后旋转。旋转前后，变化的是物体的坐标系（虚线（变换后），实线（变换前）），主要是看你要什么效果，而不是去评论它的对错。

图片来源于，《OpenGL Superblble》7th, Matrix Construction and Operators 一节；

4、OpenGL 的变换是在那个阶段发生的，如何发生

3D变换

ES 主要看红框处的顶点着色阶段即可，所以我们的变换代码是写在 Vertex Shader 的文件中。

变换转换

这里描述了三个变换阶段，第一个阶段是模型变换，第二个是视图变换阶段，第三个是投影变换阶段，最后出来的才是变换后的图形。本文讨论的是第一个阶段。

详细过程

作为了解即可

以上图片均来源于，《OpenGL Programming Guide》8th, 5. Viewing Transformations, Clipping, and Feedback 的 User Transformations 一节；

---

四、修复拉伸问题

1、改写 Shader Code

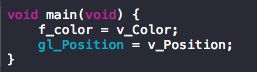
增加了一个 uniform 变量，而且是 mat4 的矩阵类型，同时左乘于顶点数据；

• 为什么使用 uniform 变量？
  • 首先， Vertex Shader 的输入量可以是 : attribute、unforms、samplers、temporary 四种;
  • 其次，我们的目的是把每一个顶点都缩小一个倍数，也就是它是一个固定的变量，即常量，所以排除 arrribute、temporary ；
  • 同时，既然是一个常量数据，那么 samplers 可以排除，所以最后使用的是 uniforms 变量；
• 为什么使用 mat4 类型？
  v_Position 是{x, y, z, w}的列向量，即为 4 x 1 的矩阵，如果要最终生成 gl_Position 也是 4 x 1 的列向量，那么就要左乘一个 4 x 4 方阵；而 mat4 就是 4 x 4 方阵。

补充：n x m · 4 x 1 -> 4 x 1，如果要出现最终 4 x 1 那么，n 必须要是 4；如果矩阵点乘成立，那么 m 必须要是 4; 所以最终结果是 n x m = 4 x 4 ;

2、应用 3D 变换知识，重新绑定数据

这里主要解决，如何给 uniform 变量赋值，而且在什么时候进行赋值的问题

核心步骤

1、在 glLinkProgram 函数之后，利用 glGetUniformLocation 函数得到 uniform 变量的 location (内存标识符);

2、从 Render Buffer 得到屏幕的像素比（宽：高）值，即为缩小的值;

3、使用 Shader Program , 调用 glUseProgram 函数;

4、使用 3D 变换知识，得到一个缩放矩阵变量 scaleMat4;

5、使用 glUniform* 函数把 scaleMat4 赋值给 uniform 变量;

• 如何给 uniform 变量赋值？

1、得到 uniform 的内存标识符

要在 glLinkProgram 后，再获取 location 值，因为只有链接后 Program 才会 location 的值

- (BOOL)linkShaderWithProgramID:(GLuint)programID {
    // 绑定 attribute 变量的下标
    // 如果使用了两个或以上个 attribute 一定要绑定属性的下标，不然会找不到数据源的
    // 因为使用了一个的时候，默认访问的就是 0 位置的变量，必然存在的，所以才不会出错
    [self bindShaderAttributeValuesWithShaderProgramID:programID];
    // 链接 Shader 到 Program
    glLinkProgram(programID);
    // 获取 Link 信息
    GLint linkSuccess;
    glGetProgramiv(programID, GL_LINK_STATUS, &linkSuccess);
    if (linkSuccess == GL_FALSE) {
        GLint infoLength;
        glGetProgramiv(programID, GL_INFO_LOG_LENGTH, &infoLength);
        if (infoLength > EmptyMessage) {
            GLchar *messages = malloc(sizeof(GLchar *) * infoLength);
            glGetProgramInfoLog(programID, infoLength, NULL, messages);
            NSString *messageString = [NSString stringWithUTF8String:messages];
            NSLog(@"Error: Link Fail %@ !", messageString);
            free(messages);
        }
        return Failure;
    }
    // 在这里
    [self.shaderCodeAnalyzer updateActiveUniformsLocationsWithShaderFileName:@"VFVertexShader"
                                                                   programID:programID];
    return Successfully;
}

- (void)updateActiveUniformsLocationsWithShaderFileName:(NSString *)fileName programID:(GLuint)programID {
    
    NSDictionary *vertexShaderValueInfos = self.shaderFileValueInfos[fileName];
    ValueInfo_Dict *uniforms = vertexShaderValueInfos[UNIFORM_VALUE_DICT_KEY];
    
    NSArray *keys = [uniforms allKeys];
    for (NSString *uniformName in keys) {
        const GLchar * uniformCharName = [uniformName UTF8String];
        // 在这里
        GLint location = glGetUniformLocation(programID, uniformCharName); 
        VFShaderValueInfo *info = uniforms[uniformName];
        info.location = location;
    }
    
}

补充：

glGetActiveUniform
void glGetActiveUniform(GLuint program, GLuint index, GLsizei bufSize, GLsizei* length, GLint* size, GLenum* type, char* name)
program 指 Shader Program 的内存标识符
index 指下标，第几个 uniform 变量，[0, activeUniformCount]
bufSize 所有变量名的字符个数，如：v_Projection , 就有 12 个，如果还定义了 v_Translation 那么就是12 + 13 = 25个
length * NULL 即可*
size 数量，uniform 的数量，如果不是 uniform 数组，就写 1，如果是数组就写数组的长度
type uniform 变量的类型，GL_FLOAT, GL_FLOAT_VEC2,GL_FLOAT_VEC3, GL_FLOAT_VEC4,GL_INT, GL_INT_VEC2, GL_INT_VEC3, GL_INT_VEC4, GL_BOOL,GL_BOOL_VEC2, GL_BOOL_VEC3, GL_BOOL_VEC4,GL_FLOAT_MAT2, GL_FLOAT_MAT3, GL_FLOAT_MAT4,GL_SAMPLER_2D, GL_SAMPLER_CUBE
name uniform 变量的变量名

// 这个函数可以得到，正在使用的 uniform 个数，即可以知道 index 是从 0 到几；
// 还有可以得到，bufSize 的长度
glGetProgramiv(progObj, GL_ACTIVE_UNIFORMS, &numUniforms);
glGetProgramiv(progObj, GL_ACTIVE_UNIFORM_MAX_LENGTH,
&maxUniformLen);

注：VFShaderValueRexAnalyzer 类就是一个方便进行调用的一种封装而已，你可以使用你喜欢的方式进行封装；

图片来源于，《OpenGL ES 2.0 Programming Guide》4. Shaders and Programs,Uniforms and Attributes 一节

• 在什么时候进行赋值操作？
  一定要在 glUseProgram 后再进行赋值操作，不然无效

- (void)drawTriangle {

    [self.shaderManager useShader];
    [self.vertexManager makeScaleToFitCurrentWindowWithScale:[self.rboManager windowScaleFactor]];
    [self.vertexManager draw];
    [self.renderContext render];
    
}

2、得到屏幕的像素比

- (CGFloat)windowScaleFactor {
    
    CGSize renderSize = [self renderBufferSize];
    float scaleFactor = (renderSize.width / renderSize.height);
    
    return scaleFactor;
    
}

补充：renderBufferSize

- (CGSize)renderBufferSize {
    GLint renderbufferWidth, renderbufferHeight;
    glGetRenderbufferParameteriv(GL_RENDERBUFFER, GL_RENDERBUFFER_WIDTH, &renderbufferWidth);
    glGetRenderbufferParameteriv(GL_RENDERBUFFER, GL_RENDERBUFFER_HEIGHT, &renderbufferHeight);
    return CGSizeMake(renderbufferWidth, renderbufferHeight);
}

3、使用 Shader Program

- (void)useShader {
    
    glUseProgram(self.shaderProgramID);
    
}

4、使用 3D 变换知识，得到一个缩放矩阵变量 scaleMat4

 VFMatrix4 scaleMat4 = VFMatrix4MakeScaleY(scale);

扩展1：

    VFMatrix4 VFMatrix4MakeXYZScale(float sx, float sy, float sz) {
        VFMatrix4 r4 = VFMatrix4Identity;
        VFMatrix4 _mat4 = {
              sx  , r4.m12, r4.m13, r4.m14,
            r4.m21,   sy  , r4.m23, r4.m24,
            r4.m31, r4.m32,   sz  , r4.m34,
            r4.m41, r4.m42, r4.m43, r4.m44,
        };
        return _mat4;
    };
    VFMatrix4 VFMatrix4MakeScaleX(float sx) {
        return VFMatrix4MakeXYZScale(sx, 1.f, 1.f);
    };
    VFMatrix4 VFMatrix4MakeScaleY(float sy) {
        return VFMatrix4MakeXYZScale(1.f, sy, 1.f);
    };
    VFMatrix4 VFMatrix4MakeScaleZ(float sz) {
        return VFMatrix4MakeXYZScale(1.f, 1.f, sz);
    };

它们都定义在：

VFMath

注：如果不想自己去写这些函数，那么可以直接使用 GLKit 提供的

数学函数

个人建议，自己去尝试写一下会更好

5、使用 glUniform 函数把 scaleMat4 赋值给 uniform 变量*

- (void)makeScaleToFitCurrentWindowWithScale:(float)scale {
    
    NSDictionary *vertexShaderValueInfos = self.shaderCodeAnalyzer.shaderFileValueInfos[@"VFVertexShader"];
    ValueInfo_Dict *uniforms = vertexShaderValueInfos[UNIFORM_VALUE_DICT_KEY];
//    NSLog(@"uniforms %@", [uniforms allKeys]);
    
    // v_Projection 投影
//    VFMatrix4 scaleMat4 = VFMatrix4Identity;
    VFMatrix4 scaleMat4 = VFMatrix4MakeScaleY(scale);
    VFMatrix4 transMat4 = VFMatrix4Identity; //VFMatrix4MakeTranslationX(0.3)
    glUniformMatrix4fv((GLint)uniforms[@"v_Projection"].location,   // 定义的 uniform 变量的内存标识符
                       1,                                           // 不是 uniform 数组，只是一个 uniform -> 1
                       GL_FALSE,                                    // ES 下 只能是 False
                       (const GLfloat *)scaleMat4.m1D);             // 数据的首指针
    
    glUniformMatrix4fv((GLint)uniforms[@"v_Translation"].location,   // 定义的 uniform 变量的内存标识符
                       1,                                           // 不是 uniform 数组，只是一个 uniform -> 1
                       GL_FALSE,                                    // ES 下 只能是 False
                       (const GLfloat *)transMat4.m1D);             // 数据的首指针

}

扩展2：

• 赋值函数有那些？
  它们分别是针对不同的 uniform 变量进行的赋值函数
  
  
  
  
  
  
  
  

3、完整工程：Github: DrawTriangle_Fix

glsl 代码分析类

核心的知识是 正则表达式，主要是把代码中的变量解析出来，可以对它们做大规模的处理。有兴趣可以看一下，没有兴趣的可以忽略它完全不影响学习和练习本文的内容。

---