本文表述了线性表及其基本操作的代码【Java实现】
参考书籍 :《数据结构 ——Java语言描述》/刘小晶 ,杜选主编
线性表需要的基本功能有:动态地增长或收缩;对线性表的任何数据元素进行访问和查找;在线性表中的任何位置进行数据元素的插入和删除操作;求线性表中指定数据元素的前驱和后继等等。
首先描述线性表的抽象类型,我们使用Java接口interface:
Ilist.java:
package liner_list;
public interface IList
{
public void clear();
public boolean isEmpty();
public int length();
public Object get(int i) throws Exception;
public void insertAt(int i,Object x) throws Exception;
public void remove(int i) throws Exception;
public int indexOf(Object x);
public void display();
}其次描述顺序表,其特点有:在线性表中的逻辑上相邻的数据元素,在物理存储位置上也是相邻的;存储密度高,但需要预先分配”足够应用“的存储空间,这可能将会造成存储空间的浪费;便于随机存储;不便于插入和删除,因为在顺序表中进行插入和删除操作会引起大量数据元素的移位。我们用SqList类描述顺序表:
SqList.java:
package liner_list;
// 规定方法中的参数i都为顺序表元素的索引(下标)
public class SqList implements IList
{
public Object[] listItem; // 顺序表存储空间
public int curLen; // 线性表的当前长度
public SqList(int maxSize)
{
listItem = new Object[maxSize]; // 为顺序表分配maxSize个存储单元
curLen = 0; // 置当前长度为0
}
public void clear()
{
curLen = 0; // 置当前长度为0,即规定为清空顺序表,但是内存中还有数据存在
}
public boolean isEmpty()
{
return curLen == 0;
}
public int length()
{
return curLen; // 返回当前长度
}
public Object get(int i) throws Exception // 得到下标为i的元素,同时判断异常
{
if (i >= curLen || i < 0) // 索引越界,0<=index<=curLen
{
throw new Exception("Argument 'i' is out of range!");
}
return listItem[i];
}
public void insertAt(int i, Object x) throws Exception // 在下表为i的位置插入元素x,同时判断异常
{
if (curLen == listItem.length) // 判断表满
{
throw new Exception("SqList is full!");
}
if (i > curLen || i < 0) // 索引越界,可以在curLen的位置进行插入
{
throw new Exception("Argument 'i' is out of range!");
}
for (int j = curLen; j > i; j--) // j从curLen的位置开始,即当前表最后一个元素的后一个位置,从而使得i位置及以后位置上的元素向后移一位
{
listItem[j] = listItem[j - 1];
}
listItem[i] = x; // 将x元素插入i位置
curLen++; // 插入后表长加一
}
public void remove(int i) throws Exception
{
if (i >= curLen || i < 0) // i小于0或者大于等于表长时抛出异常
{
throw new Exception("Argument 'i' is out of range!");
}
for (int j = i; j < curLen - 1; j++) // 从i位置开始向后,不能从最后开始,否则最后一个元素将覆盖所有元素,若想从后向前,必须将被覆盖的元素保留给下一个元素
{
listItem[j] = listItem[j + 1];
}
curLen--; // 删除完后curLen减一
}
public int indexOf(Object x) // 规定返回-1表示未找到元素x
{
for (int i = 0; i < curLen; i++)
{
if (listItem[i].equals(x))
{
return i;
}
}
return -1;
// 书本代码,效果相同
// int j = 0;
// while (j < curLen && !listItem[j].equals(x))
// {
// j++;
// }
// if (j < curLen)
// {
// return j;
// } else
// {
// return -1;
// }
}
public void display() // 输出顺序表中全部元素
{
System.out.println("****** SqList ******");
for (int i = 0; i < curLen; i++)
{
System.out.print(listItem[i] + " ");
}
System.out.println();
System.out.println("********************");
}
}接着测试我们的顺序表,使用SqListTest类来做测试:
SqListTest.java:
package liner_list;
import java.util.Scanner;
public class SqListTest
{
public static void main(String[] args) throws Exception
{
SqList sq1 = new SqList(10);
sq1.insertAt(0, "a0");
sq1.insertAt(1, "a1");
sq1.insertAt(2, "a2");
sq1.insertAt(3, "a3");
sq1.insertAt(4, "a4");
sq1.insertAt(5, "a5");
int index = sq1.indexOf("a2");
if (index != -1)
{
System.out.println("a2's index is " + index + "!");
} else
{
System.out.println("a5 is not in this SqList!");
}
sq1.display();
sq1.remove(2);
System.out.println("After remove:");
sq1.display();
SqList sq2 = new SqList(10);
Scanner sc = new Scanner(System.in);
System.out.println("Please input element:");
for (int i = 0; i < 8; i++)
{
sq2.insertAt(i, sc.next());
}
sc.close();
sq2.display();
}
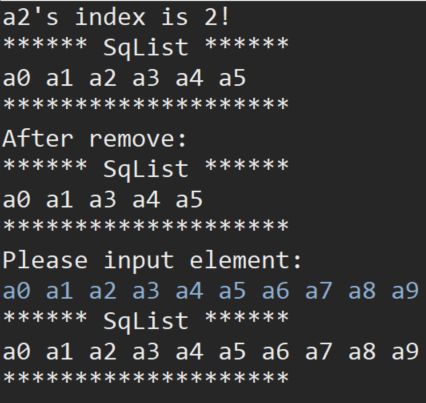
}运行我们的测试类,得到以下测试结果:
然后描述单链表,注意:我们推荐使用带头结点的单链表。这里总结以下关于头指针和头结点的问题:首先要清楚,head就是头指针,毋庸置疑;如果有头结点的话,head也头结点,这里头指针就是头结点,一般说成头指针指向头结点,而head.next是下标为0的元素,规定 head是下标为-1的元素;如果没有头结点的话,head本是就是下标为0的元素,这里没有头结点,但是head还是头指针。下面我们使用LinkList类来描述带头结点的单链表:
LinkList.java:
package liner_list;
import java.util.Scanner;
//关于头结点与头指针的问题
//首先要清楚,head就是头指针,毋庸置疑
//如果有头结点的话,head也头结点,这里头指针就是头结点,一般说成头指针指向头结点,而head.next是下标为0的元素,规定 head是下标为-1的元素
//如果没有头结点的话,head本是就是下标为0的元素,这里没有头结点,但是head还是头指针
//建议写带头结点的单链表,此类就是一个典例
public class LinkList implements IList
{
public Node head;
public LinkList() // 无参构造方法,只构建头指针
{
head = new Node();
}
public LinkList(int len, boolean Order) throws Exception // 带有两个参数的构造方法,分别为表长和插入的方式,规定true表示尾插法,flase表示头插法
{
this();
if (Order)
{
createAtEnd(len);
} else
{
createAtHead(len);
}
}
public void createAtHead(int n) throws Exception // 头插法
{
Scanner sc = new Scanner(System.in);
System.out.println("Please input element:");
for (int i = 0; i < n; i++)
{
insertAt(0, sc.next());
}
// sc.close(); // 不要关闭输入流
// display();
}
public void createAtEnd(int n) throws Exception // 尾插法
{
Scanner sc = new Scanner(System.in);
System.out.println("Please input element:");
for (int i = 0; i < n; i++)
{
insertAt(length(), sc.next());
}
// sc.close(); // 不要关闭输入流
// display();
}
@Override
public void clear() // 置空链表
{
head.data = null;
head.next = null;
}
@Override
public boolean isEmpty() // 链表判空
{
return head.next == null;
}
@Override
public int length() // 返回链表长度
{
Node p = head.next; // p指向首结点
int length = 0;
while (p != null)
{
p = p.next;
length++;
}
return length;
}
@Override
public Object get(int i) throws Exception
{
Node p = head.next;
int j = 0;
while (p != null && j < i) // 从首结点开始向后查找,直到p指向第i个结点或者p为空
{
p = p.next; // 指针后移
j++; // 计数加1
}
if (i < 0 || p == null) // i小于0或者大于表长减1时抛出异常
{
throw new Exception("Argument 'i' is out of range!");
}
return p.data;
}
@Override
public int indexOf(Object x) // 规定-1表示不在LinkList当中
{
Node p = head.next;
int index = 0;
while (p != null && !p.data.equals(x))
{
p = p.next;
index++;
}
if (p != null)
{
return index;
} else
{
return -1;
}
}
@Override
public void insertAt(int i, Object x) throws Exception
{
Node p = head; // 插入时从头结点开始,因为可以插入在下标0的位置,也可以插入在下标为表长位置
int j = -1;
while (p != null && j < i - 1) // 找出下标为i-1的结点,即i结点的前驱
{
p = p.next;
j++;
}
if (i < 0 || p == null) // i小于0或者i大于表长时抛出异常
{
throw new Exception("Argument 'i' is out of range!");
}
Node s = new Node(x);
s.next = p.next;
p.next = s;
}
@Override
public void remove(int i) throws Exception
{
Node p = head;
int j = -1;
while (p != null && j < i - 1) // 找到下标为i-1的结点,即i结点的前驱
{
p = p.next;
j++;
}
if (i < 0 || p.next == null) // 抛出条件为i小于0或者i大于表长-1,所以此处为p.next==null
{
throw new Exception("Argument 'i' is out of range!");
}
p.next = p.next.next;
}
@Override
public void display()
{
Node p = head.next;
System.out.println("****** LinkList ******");
while (p != null)
{
System.out.print(p.data.toString() + " ");
p = p.next;
}
System.out.println();
System.out.println("*********************");
}
}最后测试我们的单链表,使用LinkListTest类来做测试:
LinkListTest.java
package liner_list;
public class LinkListTest
{
public static void main(String[] args) throws Exception
{
LinkList linkList = new LinkList(10, true);
linkList.remove(0);
linkList.remove(1);
linkList.remove(linkList.length() - 1);
System.out.println("After remove:");
linkList.display();
linkList.insertAt(linkList.length(), "a9");
System.out.println("After insert:");
linkList.display();
int index = linkList.indexOf("a2");
if (index != -1)
{
System.out.println("a2's index is " + index + "!");
} else
{
System.out.println("a2 is not in this LinkList!");
}
}
}运行我们的测试类,得到以下结果:
以上便是线性表中顺序表和单链表最基础的代码描述,算法思想本文中没有写到,大家可以去看看前面说的那本参考书籍。此系列后面会陆续介绍更多有关数据结构的内容,也会更新一些关于数据结构的算法题目例子,谢谢大家支持!