《Java语言程序设计》编程练习6.31（财务应用程序：信用卡号的合法性）

6.31（财务应用程序：信用卡号的合法性）信用卡号遵循下面的模式。一个信用卡号必须是13到16位的整数。它的开头必须是：

• 4，指Visa卡
• 5，指Master卡
• 37，指American Express卡
• 6，指Discover卡

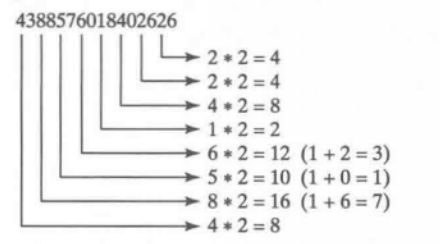
      在1954年，IBM的Hans Luhn提出一种算法，该算法可以验证信用卡号的有效性。这个算法在确定输入的卡号是否正确，或者这张信用卡号是否被扫描仪正确扫描方面是非常有用的。遵循这个合法性检    测可以生成所有的信用卡号，通常称之为Luhn检测或者Mod 10检测，可以如下描述（为了方便解释，假设卡号为4388576018402626)：

1）从右到左对每个数字翻倍。如果对某个数字翻倍之后的结果是一个两位数，那么就将这两位加在一起得到一位数。

 

2) 现在将第一步得到的所有一位数相加。
　　　　　　4+4+8+2+3+1+7+8=37
3) 将卡号里从右到左在奇数位上的所有数字相加。
　　　　　　6+6+0+8+0+7+8+3=38
4) 将第二步和第三步得到的结果相加。
　　　　　　37+38=75
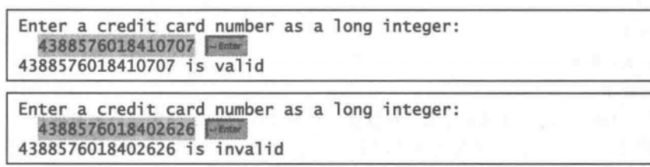
5) 如果第四步得到的结果能被10整除，那么卡号是合法的；否则，卡号是不合法的。例
如，号码4388576018402626是不合法的，但是号码4388576018410707是合法的。

编写程序，提示用户输入一个long型整数的信用卡号码，显示这个数字是合法的还是非法
的。使用下面的方法设计程序：

 1 /** Returntrue if the card number is valid */
 2 public static boolean isVa1id(long number)
 3 
 4 /** Getthe result from Step2 */
 5 public static int sumOfDoubleEvenPIace(long number)
 6 /** Return this number if it is a single digit, otherwise,
 7 * return the sum of the two digits*/
 8 public static int getDigit(int number)
 9 /** Returnsum ofodd-placedigitsin number */
10 public static int sumOfOddPlace(1ong number)
11 /** Returntrue if the digitd is a prefix for number */
12 public static boolean prefixMatched(1ong number, int d)
13 /** Returnthe number ofdigitsin d */
14 public static int getSize(1ong d)
15 /** Return the first k number ofdigitsfrom number. If the
16 * number ofdigitsin number is less than k, return number. */
17 public static long getPrefix(long number, int k) 

下面是程序的运行示例：（你也可以通过将输人作为一个宇符串读人，以及对宇符串进行处
理来验证信用卡卡号。

 

 

以下为实现这功能的代码：

  1 /**     fileName:   creditCardVerify.java
  2  *       作用:      计算信用卡号的合法性
  3  *      mail:       [email protected]
  4  *      说明：      信用卡号必须是13到16位，开头必须是4，5，37，6
  5  *                          
  6  */
  7 
  8 import java.util.Scanner;
  9 
 10 public class creditCardVerify{
 11     public static void main(String[] args) {
 12         Scanner input = new Scanner(System.in);
 13         System.out.print("请输入卡号，按Enter结束输入: ");
 14         long i = input.nextLong();
 15         if (isValid(i))
 16             System.out.println(i + " is valid");
 17         else
 18             System.out.println(i + " is invalid");
 19     }
 20 
 21     /** Return true if the card number is valid */
 22     /** 返回ture表明这个卡号是有效的 */
 23     public static boolean isValid(long number) {
 24         if(prefixMatched(number)){
 25             if(sumOfdoubleEvenPlace(number)%10 == 0)
 26                 return true;
 27         }
 28         return false;
 29     }
 30 
 31     /**
 32      * Get the result from Step 2 从步骤2得到结果？。双重偶数之和
 33      */
 34     public static int sumOfdoubleEvenPlace(long number) {
 35         int sum = 0;
 36         int sumGetdigit = 0;
 37         long temp = 0;
 38         int numberSize = getSize(number);
 39         for(int i =2; i <= numberSize; i += 2){
 40             temp = getPrefix(number, i);
 41             sumGetdigit += getDigit((int)temp*2);
 42         }
 43         sum = sumGetdigit + sumOfOddPlace(number);
 44         return sum;
 45     }
 46 
 47     /**
 48      * Retrun this number if it is a single digit, otherwise, Return the sum of the
 49      * two digits
 50      * 
 51      * 如果是单个数字，则返回该数字，否则返回两位数的和。获得数字
 52      */
 53     public static int getDigit(int number) {
 54         int numGetDigit = 0;
 55         if(number % 10 >= 0){
 56             numGetDigit = number % 10;
 57             number /= 10;
 58             numGetDigit += number;
 59             return numGetDigit;
 60         }
 61         return number;
 62     }
 63 
 64     /**
 65      * Return sum of odd-place digits in number 返回卡号总右往左的奇位数之和
 66      */
 67     public static int sumOfOddPlace(long number) {
 68         int sum = 0, i = 0;
 69         int Size = getSize(number);
 70 
 71         for(i = 1; i <= Size; i+=2){
 72             sum += getPrefix(number, i);
 73         }
 74         return sum;
 75     }
 76 
 77     /**
 78      * Return true if the digit d is a prefix for number 判断卡号的前缀是否合法
 79      */
 80     public static boolean prefixMatched(long number) {
 81         int numberSize = getSize(number); 
 82         if(numberSize >= 13 && numberSize <= 16){
 83             switch((int)getPrefix(number, numberSize)){
 84                 case 4: return true;
 85                 case 5: return true;
 86                 case 6: return true;
 87                 case 3: if((int)getPrefix(number, numberSize -1) == 7)
 88                         return true;
 89             }
 90         }
 91         return false;
 92     }
 93 
 94     /** Return the number of digits in d 
 95      * 获得信用卡号的长度并将结果返回
 96     */
 97     public static int getSize(long d){
 98         long i= 0;
 99         while(d > 0){
100             i += 1;
101             d /= 10;
102         }
103         return (int)i; 
104     }
105 
106     /** Return the first k number of digits from number. If the 
107      *  Number of digits in number is less than k, return number.
108      * 从数字中返回第一个k位数。如果数字总的位数小于k，则返回数字。
109      * 应该是获得信用卡号的第k位的字母
110      */
111     public static long getPrefix(long number, int k){
112         int i = 0;
113         long temp=0;
114         while (i < k){
115             i++;
116             temp = number % 10;
117             number /= 10;   
118         }
119         return temp;
120     }
121 }