树状数组 | 入门介绍篇

一. 问题引入：

题目一：

有n个正整数，编号从1开始，用A[1]、A[2]……A[n]表示。
修改：无
查询：共有q次询问，每次查询编号从L到R的所有数之和为多少？其中1<= L <= R <= n。

这道题目很简单，就是求区间[L,R]数的总和。

方法一：暴力循环

直接用一个双重循环，暴力求出。
这样，对于每次询问，需要将(R-L+1)个数相加，时间复杂度为。那么，对于q次查询，总的时间复杂度就为。

方法二：前缀和

求前缀和，令 S[0]=0, S[1]=A[1]， ，那么

这样，对于每个询问，就只需要做一次减法，大大提高效率。

---

题目二：

有n个正整数，编号从1开始，用A[1]、A[2]……A[n]表示。
修改：共有w次修改，每次修改将第x个数增加C。
查询：共有q次询问，每次查询编号从L到R的所有数之和为多少？其中1<= L <= R <= n。

对于这个问题，就变得复杂了一点，我们还是用前面两种方法。

对于方法一，修改只需要修改对应的A[x]的值，每一次的询问仍需要用一个循环求出。
修改的时间复杂度为，询问的时间复杂度为。

对于方法二，每一次的询问只需要做一次减法，时间复杂度为
而修改的话就比较麻烦，假如A[L]+=C之后，S[L],S[L+1],……,S[R]都需要增加C,全部都要修改，时间复杂度为。

对比两种方法，最终的时间复杂度都是相同的。但是，两种方法有各自的特点，方法一修改快，求和慢。 方法二求和快，修改慢。

那么，是否有一种更好的方法，将这两种的优点结合起来呢？答案是肯定的，树状数组就是其中的一种做法。

---

二. lowbit函数：

lowbit(x)—— x的二进制表达式中最低位的1所对应的值。

举个例子，6的二进制是，那么。这里的下标分别表示二进制和十进制。

那么，怎么求出lowbit呢？这里有两种方法。

方法一：
首先，你必须知道如何消除二进制中最后一个位1，利用n &= (n - 1)就可以做到。然后看一下消了几次n变成0，次数就是答案。

n &= (n - 1)具体的操作是把最后一位1变成0，后面的0变成1，与运算一下，最后一位1就消掉了。

class Solution 
{
public:
     int  NumberOf1(int n) 
     {
         int ret = 0;
         for (; n; n &= (n - 1), ret++);
         return ret;
     }
};

简化一下代码，

int lowbit(x) 
{   
    return x - (x & (x - 1));
}

对于第一种方法，我暂时不理解，就先贴着吧，那位大佬知道还望赐教。放个地址：参考博客

方法二：

求负数的补码的简便方法：把这个数的二进制写出来，然后从右向左找到第一个1(这个1就是我们要求的结果，但是现在表示不出来，后来的操作就是让这个1能表示出来)，这个1不要动和这个1右边的二进制不变，左边的二进制依次取反，这样就求出的一个数的补码。

说这个方法主要是让我们理解一个负数的补码在二进制上的特征 。

然后我们把这个负数对应的正数与该负数进行与运算，由于这个1的左边的二进制与正数的原码对应的部分是相反的，所以两者相与一定都为0；由于这个1和这个1右边的二进制都是不变的，相与后还是原来的样子。因此，最后得到的结果就是lowbit(x)的值。

下面还是举个例子更好理解，如图所示，lowbit(20)=4。

// 代码实现
int lowbit(x) 
{   
    return x & -x;
}

---

三. 树状数组——Binary Indexed Tree(B.I.T)

上面说了那么多，接下来就是重头戏——树状数组了。

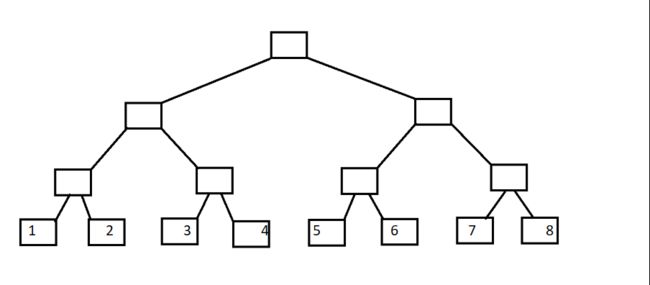
树状数组的关键就在于树状，那么是什么树呢，最简单的就是我们熟悉的二叉树。

我们用二叉树的叶子结点来代表A数组，分别为A[1]~A[8]。

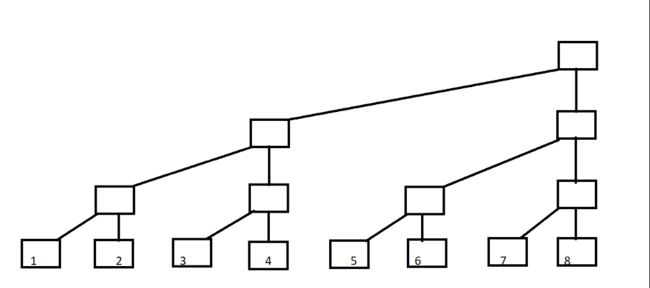
现在，将上图稍微变形一下。

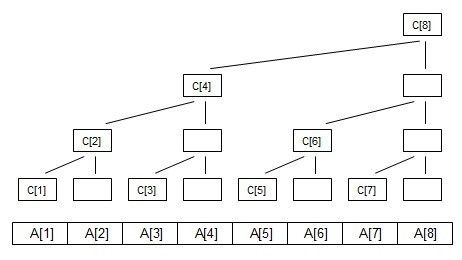
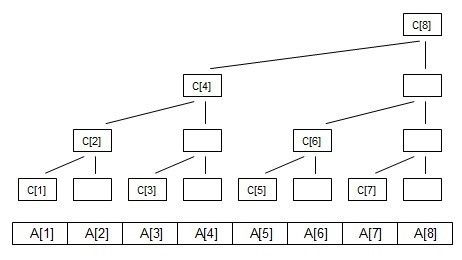
现在，用每一列的顶端节点来表示C数组，分别为C[1]~C[8]，如下图。

可以看出来，其实C数组就是我们说的树状数组。

---

下面，我们来具体分析一下，假设C[i]代表以i节点为根节点的子树，其所有叶子节点的权值之和（实际C数组的含义，依具体题目而定）。

根据上图，我们可以知道：

上面说了很多的二进制，那么我们将C数组的下标转为二进制。

好像也没什么不一样，但是，当我们仔细看的时候，会发现每个C[i]的值，其实就对应着lowbit(i)个A数组元素的和，且从A[i]开始向着A[i-1]、A[i-2]方向递减。
【Tips：可以根据树的结构来理解，以节点i为根节点的子树，将其所有叶子节点相加，就是i节点的值】

也就是说

这样子看可能还不够直观，那么我们可以举一个例子来看一下。

当i=5时，二进制为101，lowbit(5)=1，只有一个A数组元素参与加和，且A数组的下标从当前的i=5开始，那么C[5]=A[5]。
当i=6时，二进制为110，lowbit(6)=2，有两个A数组元素参与加和，且A数组的下标从当前的i=6开始，那么C[6]=A[6]+A[5]。
i的其他取值情况依次类推。

---

四. 区间查询【向下维护】

回到一开始的题目，那么，如何用树状数组来求解呢。

这里先定义一个sum数组，sum[i]表示前i个A数组元素的和。

下面举些例子，

• 
  

整理一下，

再转换成二进制，

以i=7为例进行演示：

start	7(111)	ans+=C[7]
lowbit(7)=001	7-lowbit(7)=6(110)	ans+=C[6]
lowbit(6)=010	6-lowbit(6)=4(100)	ans+=C[4]
lowbit(4)=100	4-lowbit(4)=0(000)	end

下面给出代码：

int find(int x)
{
    int ans=0;
    for(int i=x;i>0;i-=lowbit(i)) 
        ans+=C[i];
    return ans；
}

---

五. 单点更新【向上维护】

当我们修改A数组中的某一个值时，应当如何来更新C数组呢？

回想上面的区间查询过程，我们可以发现，单点更新其实就是区间查询的逆过程，区间查询是向下维护子树，而单点修改需要向上维护。

当更新A[1]的值时 需要向上更新C[1] ,C[2],C[4],C[8]的值。

	1(001)	C[1]+=y
lowbit(1)=001	1+lowbit(1)=2(010)	C[2]+=y
lowbit(2)=010	2+lowbit(2)=4(100)	C[4]+=y
lowbit(4)=100	4+lowbit(4)=8(1000)	C[8]+=y

// x：修改的位置(A数组)
// y：修改的值
void change(int x,int y)
{
    for(int i=x;i<=n;i+=lowbit(i))
        C[i]+=y;
}

六. 写在最后：

资料参考：

• 博客：https://blog.csdn.net/qq853674765/article/details/70050306（lowbit函数）
• 博客：https://blog.csdn.net/Small_Orange_glory/article/details/81290634（树状数组）
• 博客：https://blog.csdn.net/flushhip/article/details/79165701#（树状数组）

上述的数组C就是我们说的树状数组(怕内容太多混淆大家，逃)，利用二进制/二叉树，使得查询、更新的时间复杂度都在。

再一次感受到了二进制的神奇魔力，lowbit函数的第一种方法暂时还无法理解，就先贴着吧，自己再琢磨琢磨，其实我个人还是更加喜欢第二种方法。

如有错误，还望大家指出。