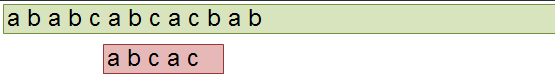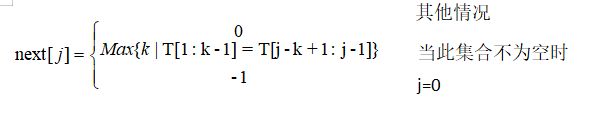问题描述
KMP是解决子串的定位操作的一种算法,即在一个字符串中找到另一个字符串出现的位置,如果找不到就返回-1.我们使用的例子如下:主串为ababcabcacbab,
子串为abcac。
符号标记
| 符号 | 描述 |
|---|---|
| S | 主串 |
| T | 子串 |
| i | 主串的下标 |
| j | 子串的下标 |
传统做法
传统做法同时遍历子串T和主串S,记i,j分被为主串和子串的下标,如果S[i]==S[j],则同时执行i++和j++;如果S[i]!=S[j]则将原先主串的开始遍历处的下标+1,重新开始比较。如下图:
当S[2]!=T[2]时,我们将T向右移动一个单位并重复上述操作。
这样不断重复直到子串全部匹配完毕返回子串位置,或者遍历超过了主串的长度,返回-1。
int indexOf_1(string S,string T){
int i=0;
int j=0;
while (i=T.size()) return i-j;
else -1;
}
int main(){
string S = "ababcabcacbab";
string T = "abcac";
cout< 传统方法的弊端
拿我们的例子来说,假如传统方法遍历时,出现了以下一幕:
我们比较了子串的a b c a 前五个字符但是但比较第5个字符时出现了不相等的情况,于是我们将子串向右移动一位再进行比较。这样不断重复直到:
现在我们可以思考一个问题,当我们遇到第一幅图的情况时,其实我们是已经知道移动子串两次的开始字符分别为b和c,这个信息就存储子串当中,因为我们经过第一幅图的比较就已经确定了子串的bc与主串的bc相匹配。那么我们怎么样利用上这个信息,使得子串的移动不是1个单位1个单位的移,而是根据上一次匹配得到信息,直接跳过某些字符的匹配。下面我们就来探讨下两个问题。
问题一:子串滑动多大距离
当我们比较主串和子串的某个字符时,如果两个字符不相等我们应该将子串向右滑动几个单位。即若S[i]!=T[j],我们滑动子串使得S[0:i]=T[0:k],我们现在来确定k的大小。通过上一次不成功的比较,我们得到了如下结论S[i]!=T[j],因为子串已经比较到j了所以j前面的已经全都匹配上了。即:S[i-j:i-1]==T[1:j-1]。但我们滑动子串使得i与k相比较时,我们必须保证S[i-k:i-1]==T[1:k-1].我们用下图来表示这三者之间的关系。
在j和k左边上下都是相互匹配的,通过图我们可以很清楚的看到,移动后的子串与原先的子串在绿色部分也是相互匹配的。即:T[1:k-1]=T[j-k+1:j-1]。
这样我们就可以通过一个next数组保存子串的匹配信息。next[j]=k表示当子串的T[j]与主串S[i]不匹配时,向右移动多个单位使T[k]与S[i]进行匹配。如果T[k]!=S[i],则继续使得T[next[k]]与S[i]相比较。
next的计算公式如下:
注:这里公式中的-1指的是当子串与主串在第一个字符处就不相等时,子串向右移动一个单位,即相当于原先子串-1处的字符与主串i处字符比较。实际上-1处是无效的。这里只是做一个标记,当遇到next[j]=-1时,子串滑动一个单位。
问题二:如何求子串的next值
通过问题一中的分析我们可以知道子串中的next的值只与子串本身有关即T[1:k-1]=T[j-k+1:j-1]中只包含T的字符。现在我们可以确定的是next(0)=-1.
我们可以据此来完成递推。即已知next[j]=k,求next[j+1]。
分两种情况讨论。
- 当T[k]=T[j],这时next[j+1]=k+1=next[j]+1,画图表示如下。
其中蓝色部分表示T[1:k-1]=T[j-k+1:j-1]这是通过next[j]=k得出的。(这里需要注意的是需要理解next[j]=k只表示j(或者k)之前的一段字符相等,并不能得出k和j两处的关系,具体的公式得出可以看看问题一中的推导)。
这时若T[k]=T[j],图中的蓝色部分向右扩展一个单位得出T[1:k]=T[j-k+1:j]:
于是有next[j+1]=next[j]+1
- 当T[k]!=T[j],next[j+1]=next[k]+1,k=next[k](重复使得T[next[k]]==T[j])。这里也很好理解既然T[k]!=T[j],那我们就可以再从前面找到一个值k',使得T[k']==T[j],k'的前面某一段必须与j前面相同的一段相同,同样也与k前面某一段相同,根据k,k'前拥有相同的一段就可以根据next[k]求出k'。
上面的两种情况我们也可以将其看作是子串和主串的匹配问题。只不过子串和主串都是T的某一段。
代码部分
//求next数组
void getNext(string T,int next[],int len){
next[0]=-1;
int k=-1;
int j=0;
while(j=size) return i-j;
else return -1;
}
int main(){
string S = "ababaababcacbcacbab";
string T = "ababcac";
int index2 = kmp(S,T);
cout< 小结
传统的算法的最坏情况下时间复杂度是O(m*n),当一般这种情况不多见。KMP算法的时间复杂度是O(m+n)。