一 可以创建多少个线程
能创建的线程数的具体计算公式如下:
(MaxProcessMemory - JVMMemory - ReservedOsMemory) / (ThreadStackSize) = Number of threads
MaxProcessMemory:指的是一个进程的最大内存,在32位的 windows下是 2G
JVMMemory:JVM堆内存大小,即配置的-Xms 最小堆内存和-Xmx 最大堆内存。
ReservedOsMemory:保留的操作系统内存
ThreadStackSize:-Xss 设置每个线程的堆栈大小。JDK5.0以后每个线程堆栈大小为1M
由多线程内存溢出产生的实战分析 https://www.jianshu.com/p/54cdcd0fc8a6
JVM最大线程数 https://www.cnblogs.com/princessd8251/articles/3914434.html
二 Redis相关深入
深入学习Redis(3):主从复制 https://www.cnblogs.com/kismetv/p/9236731.html
三 MySQL数据量大时,delete操作无法命中索引
数据量无论多还是少时,select查询操作都能命中索引:
、数据量少时,delete操作能命中索引
但是数据量特别大时,delete操作便没办法命中索引:
一条SQL语句走哪条索引是通过其中的优化器和代价分析两个部分来决定的。所以,随着数据的不断变化,最优解也要跟着变化。因此如果优化器计算出花费时间太长,就不会使用索引。
对于查询情况,其实MySQL提供给我们一个功能来引导优化器更好的优化,那便是MySQL的查询优化提示(Query Optimizer Hints)。比如,想让SQL强制走索引的话,可以使用 FORCE INDEX 或者USE INDEX;它们基本相同,不同点:在于就算索引的实际用处不大,FORCE INDEX也得要使用索引。
EXPLAIN SELECT * FROM yp_user FORCE INDEX(idx_gender) where gender=1 ;
同样,你也可以通过IGNORE INDEX来忽略索引。
EXPLAIN SELECT * FROM yp_user IGNORE INDEX(idx_gender) where gender=1 ;
虽然有MySQL Hints这种好用的工具,但我建议还是不要再生产环境使用,因为当数据量增长时,你压根儿都不知道这种索引的方式是否还适应于当前的环境,还是得配合DBA从索引的结构上去优化。
四 Java内存模型之happens-before
JMM使用happens-before的概念来阐述多线程之间的内存可见性。
在JMM中,如果一个操作执行的结果需要对另一个操作可见,那么这两个操作之间必须存在happens-before关系。
happens-before原则非常重要,它是判断数据是否存在竞争、线程是否安全的主要依据,依靠这个原则,我们解决在并发环境下两操作之间是否可能存在冲突的所有问题。这里提到的两个操作既可以是在一个线程之内,也可以是在不同线程之间。
1 i = 1; //线程A执行 2 j = i ; //线程B执行
例如对于上面的操作,假定使线程A执行1代码,线程B执行2代码。那么j 是否等于1呢?
假定线程A的操作(i = 1)happens-before线程B的操作(j = i),那么可以确定线程B执行后 j = 1 一定成立,
如果A的操作和B的操作不存在happens-before原则,那么j = 1 不一定成立。
happens-before原则定义如下:
1. 如果一个操作happens-before另一个操作,那么第一个操作的执行结果将对第二个操作可见,而且第一个操作的执行顺序排在第二个操作之前。
2. 两个操作之间存在happens-before关系,并不意味着一定要按照happens-before原则制定的顺序来执行。如果重排序之后的执行结果与按照happens-before关系来执行的结果一致,那么这种重排序并不非法。
下面是happens-before原则规则:
1. 程序次序规则:一个线程内,按照代码顺序,书写在前面的操作先行发生于书写在后面的操作;
2. 锁定规则:一个unLock操作先行发生于后面对同一个锁的lock操作;
3. volatile变量规则:对一个变量的写操作先行发生于后面对这个变量的读操作;
4. 传递规则:如果操作A先行发生于操作B,而操作B又先行发生于操作C,则可以得出操作A先行发生于操作C;
5. 线程启动规则:Thread对象的start()方法先行发生于此线程的每个一个动作;
6. 线程中断规则:对线程interrupt()方法的调用先行发生于被中断线程的代码检测到中断事件的发生;
7.线程终结规则:线程中所有的操作都先行发生于线程的终止检测,我们可以通过Thread.join()方法结束、Thread.isAlive()的返回值手段检测到线程已经终止执行;
8. 对象终结规则:一个对象的初始化完成先行发生于他的finalize()方法的开始;
上面八条是原生Java满足Happens-before关系的规则,但是我们可以对他们进行推导出其他满足happens-before的规则:
1. 将一个元素放入一个线程安全的队列的操作Happens-Before从队列中取出这个元素的操作
2. 将一个元素放入一个线程安全容器的操作Happens-Before从容器中取出这个元素的操作
3. 在CountDownLatch上的倒数操作Happens-Before CountDownLatch#await()操作
4. 释放Semaphore许可的操作Happens-Before获得许可操作
5. Future表示的任务的所有操作Happens-Before Future#get()操作
6. 向Executor提交一个Runnable或Callable的操作Happens-Before任务开始执行操作
如果两个操作不存在上述(前面8条 + 后面6条)任一一个happens-before规则,那么这两个操作就没有顺序的保障,JVM可以对这两个操作进行重排序。如果操作A happens-before操作B,那么操作A在内存上所做的操作对操作B都是可见的。
private int i = 0; public void write(int j ){ i = j; } public int read(){ return i; }
约定线程A执行write(),线程B执行read(),且线程A优先于线程B执行,那么线程B获得结果是什么?
我们就这段简单的代码一次分析happens-before的规则(规则5、6、7、8 + 推导的6条可以忽略,因为他们和这段代码毫无关系):
1、由于两个方法是由不同的线程调用,所以肯定不满足程序次序规则;
2、两个方法都没有使用锁,所以不满足锁定规则;
3、变量i不是用volatile修饰的,所以volatile变量规则不满足;
4、传递规则肯定不满足;
所以我们无法通过happens-before原则推导出线程A happens-before线程B,虽然可以确认在时间上线程A优先于线程B执行,但是就是无法确认线程B获得的结果是什么,可能获得0,也可能获得线程A指定的值,所以这段代码不是线程安全的。
因此如果想使该端代码满足A操作happens-before B操作,则只需满足规则2、3任一即可。,例如变量 i 定义为volatile类型的或者两个方法均加锁。
面试题:
public class ThreadSafeCache { int result; public int getResult() { return result; } public synchronized void setResult(int result) { this.result = result; } public static void main(String[] args) { ThreadSafeCache threadSafeCache = new ThreadSafeCache(); for (int i = 0; i < 8; i++) { new Thread(() -> { int x = 0; while (threadSafeCache.getResult() < 100) { x++; } System.out.println(x); }).start(); } try { Thread.sleep(1000); } catch (InterruptedException e) { e.printStackTrace(); } threadSafeCache.setResult(200); } }
在上面代码中,只对setResult操作加锁,而getResult操作未加锁,在main函数中,起了多个线程执行getResult方法,而在主线程中执行setResult操作。执行结果是子线程一直在执行while操作,无法返回。
问题解析:由于只对setResult操作加锁,而getResult操作未加锁,因此不同线程的set和get操作不满足happens-before原则,因此,多线程并发的同时进行set、get操作,A线程调用set方法,B线程调用get方法并不一定能对这个改变可见!!!
从而导致main线程执行的set操作改变的值无法对子线程可见,即main线程的set操作只是将值更新到main线程的缓存中,而子线程的get操作仍然是从各自的缓存中获取。
解决办法:(1)get操作也加锁,这时便可以满足happens-before原则2:一个unLock操作先行发生于后面对同一个锁的lock操作,从而可见。
(2)变量使用volatile修饰,从而满足happens-before原则3:对一个变量的写操作先行发生于后面对这个变量的读操作,从而可见。
参考:1、阿里一道Java并发面试题 https://mp.weixin.qq.com/s/i9ES7u5MPWCv1n8jYU_q_w
2、【死磕Java并发】-----Java内存模型之happens-before https://www.cnblogs.com/chenssy/p/6393321.html
五 B树和B+树的插入删除操作
B树和B+树的插入、删除图文详解 https://www.cnblogs.com/nullzx/p/8729425.html
从MySQL Bug#67718浅谈B+树索引的分裂优化 http://hedengcheng.com/?p=525
1 B-Tree的插入分裂过程和优化
B-Tree的插入和分裂过程:
标准的B-Tree分裂时,将一半的键值和数据移动到新的节点上去。原有节点和新节点都保留一半的空间,用于以后的插入操作。当按照键值的顺序插入数据时,左侧的节点不可能再有新的数据插入。因此,会浪费约一半的存储空间。
解决这个问题的基本思路是:分裂顺序插入的B-Tree时,将原有的数据都保留在原有的节点上。创建一个新的节点,用来存储新的数据。
2 传统B+Tree的插入分裂过程
继续插入记录6,7,B+树结构会产生以下的一系列变化:
插入记录6,新的B+树结构如下:
插入记录7,由于叶页面中只能存放4条记录,插入记录7,导致叶页面分裂,产生一个新的叶页面。
传统B+树页面分裂操作分析:
按照原页面中50%的数据量进行分裂,针对当前这个分裂操作,3,4记录保留在原有页面,5,6记录移动到新的页面。最后将新纪录7插入到新的页面中;
50%分裂策略的优势:
分裂频率较大:针对如上所示的递增插入(递减插入),每新插入两条记录,就会导致最右的叶页面再次发生分裂;
3 B+树分裂操作的优化
由于传统50%分裂的策略,有不足之处,因此,目前所有的关系型数据库,包括Oracle/InnoDB/PostgreSQL,都针对B+树索引的递增/递减插入进行了优化。经过优化,以上的B+树索引,在记录6插入完毕,记录7插入引起分裂之后,新的B+树结构如下图所示:
对比上下两个插入记录7之后,B+树索引的结构图,可以发现二者有很多的不同之处:
2、原有页面的利用率,仍旧是100%;
优化分裂策略的优势:
索引分裂的代价小:不需要移动记录;
索引分裂的概率降低:如果接下来的插入,仍旧是递增插入,那么需要插入4条记录,才能再次引起页面的分裂。相对于50%分裂策略,分裂的概率降低了一半;
索引页面的空间利用率提高:新的分裂策略,能够保证分裂前的页面,仍旧保持100%的利用率,提高了索引的空间利用率;
优化分裂策略的劣势:
如果新的插入,不再满足递增插入的条件,而是插入到原有页面,那么就会导致原有页面再次分裂,增加了分裂的概率。
因此,此优化分裂策略,仅仅是针对递增递减插入有效,针对随机插入,就失去了优化的意义,反而带来了更高的分裂概率。
在InnoDB的实现中,为每个索引页面维护了一个上次插入的位置,以及上次的插入是递增/递减的标识。根据这些信息,InnoDB能够判断出新插入到页面中的记录,是否仍旧满足递增/递减的约束,若满足约束,则采用优化后的分裂策略;若不满足约束,则退回到50%的分裂策略。
但是,InnoDB的实现,有不足之处,会导致下面提到的一个Bug。
4 优化后的B+Tree可以存在的问题及解决办法
在特定的插入情况下,InnoDB的索引页面利用率极低,这是由于InnoDB不正确的使用优化分裂策略导致的。
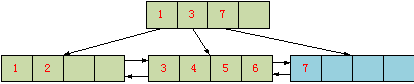
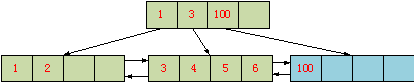
考虑以下的一个B+树,已有的用户数据是1,2,3,4,5,6,100,并且在插入记录100之后,引起索引页面分裂,记录100在分裂后被插入到新的页面:
由于插入100能够满足递增的判断条件,因此采用了优化分裂策略,分裂不移动数据,新纪录100插入到新页面之中,原有页面的最后插入位置仍旧是6号记录不变,原有页面仍旧保持递增的插入标识不变。
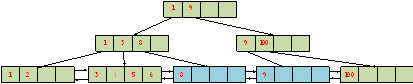
此时,考虑连续插入9,8,7这几条记录,会得到什么样的B+树?此时,全局递增插入变为全局递减插入。
插入记录9后的B+树结构:
由于InnoDB的B+树,上层节点保存的是下层页面中的最小值(Low Key),因此记录9仍旧会插入到【3,4,5,6】页面,此时页面已满,需要分裂。而且判断出记录9仍旧满足页面中的递增判断条件(Last_Insert_Pos = 6,9插入到6之后,并且原来是递增插入的)。因此,采用优化的分裂策略,产生新的页面插入记录9,原有页面记录保持不变。
插入记录8后的B+树结构:
插入记录7,也一样。采用优化的分裂策略,记录7独占一个页面。
是页面的利用率极低,每个索引叶页面,只能存放一条记录;
主要原因
InnoDB错误的采用了优化的索引分裂策略。InnoDB判断是否满足递增/递减的插入模式,采用的是页面级的判断,哪怕全局的模式发生了变化,只要页面内记录的模式未变,仍旧会选择优化后的索引分裂策略;
解决办法:
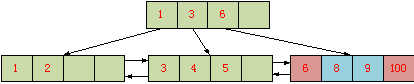
解决方案是:每次分裂,若插入的记录是页面中的最后一条记录,则至少将此记录前一条记录分裂到新页面之中。采用此策略,针对100,9,8这一个系列的插入,会产生以下的系列B+树:
插入100,9,8后的B+树:
插入100时,移动原有页面最后一条记录到新的页面(将6移动到新页面),此时新页面中的记录为【6,100】。接下来插入9,8,都会插入到新的页面之中,不会产生分裂操作,空间利用率提高,减少了索引页面分裂,解决了Bug#67718的问题。
六 数据操作在B+ tree上的实现
索引实现原理(索引的产生流程) https://blog.csdn.net/timer_gao/article/details/78013826
(1)用主键查询
直接在主键索引Clustered B+Tree上查询。
(2)用辅助索引查询
A. 在Secondary B+Tree上查询到主键。
B. 用主键在Clustered B+Tree上查询对应数据页的数据
可以看出,在使用主键值替换页指针后,辅助索引的查询效率降低了。因为会有一个回表的操作。
A. 尽量使用主键来查询数据(索引遍历操作除外)。
B. 可以通过缓存来弥补性能,因此所有的键列,都应该尽量的小。
(3)插入INSERT操作
A. 在Clustered B+Tree上插入数据。
B. 在所有其他Secondary B+Tree上插入主键。
(4)DELETE删除操作
A. 在Clustered B+Tree上删除数据
B. 在所有其他Secondary B+Tree上删除主键。
(5)UPDATE 非主键列
A. 在Clustered B+Tree上更新数据。
(6)UPDATE 主键列
A. 在Clustered B+Tree删除原有的记录(只是标记为DELETED,并不真正删除)。
B. 在Clustered B+Tree插入新的记录。
C. 在每一个Secondary B+Tree上删除原有的主键。(有疑问,看下一节。)
D. 在每一个Secondary B+Tree上插入新的主键。
(7)UPDATE 辅助索引的键值
A. 在Clustered B+Tree上更新数据。
B. 在每一个Secondary B+Tree上删除原有的主键。
C. 在每一个Secondary B+Tree上插入新的主键。
更新主键列时,需要更新多个页,效率比较低。
A. 尽量不用对主键列进行UPDATE操作。
B. 更新很多时,尽量少建索引。
七 DNS解析过程
1、DNS是什么
DNS (Domain Name System 的缩写)的作用非常简单,就是根据域名查出IP地址。你可以把它想象成一本巨大的电话本。
举例来说,如果你要访问域名 math.stackexchange.com,首先要通过DNS查出它的IP地址是 151.101.129.69。
http://www.ruanyifeng.com/blog/2016/06/dns.html
八 位运算
1、位运算介绍
1. 字节:byte:用来计量存储容量的一种计量单位;位:bit
2. 一个字节等于8位 1byte = 8bit
java中类型占多少位:https://blog.csdn.net/m0_37479246/article/details/79492828
(1)与运算(&)
参加运算的两个数据,按二进制位进行“与”运算。
运算规则:0 & 0 = 0; 0 & 1 = 0; 1 & 0 = 0; 1 & 1 = 1;
即:两位同时为“1”,结果才为“1”,否则为0
例如:3&5 即 0000 0011 & 0000 0101 = 0000 0001 因此,3&5的值得1。
例如:9&5 即 0000 1001 (9的二进制补码)&00000101 (5的二进制补码) =00000001 (1的二进制补码)可见9&5=1。
(2)或运算(|)
参加运算的两个对象,按二进制位进行“或”运算。
运算规则:0 | 0 = 0; 0 | 1 = 1; 1 | 0 = 1; 1 | 1 = 1;
即 :参加运算的两个对象只要有一个为1,其值为1。
例如:3|5 即 0000 0011 | 0000 0101 = 0000 0111 因此,3|5的值得7。
例如:9|5可写算式如下: 00001001|00000101 =00001101 (十进制为13)可见9|5=13
(3)异或运算(^)
参加运算的两个数据,按二进制位进行“异或”运算。
运算规则:0 ^ 0 = 0; 0 ^ 1 = 1; 1 ^ 0 = 1; 1 ^ 1 = 0;
即:参加运算的两个对象,如果两个相应位为“异”(值不同),则该位结果为1,否则为0。
例如:9^5可写成算式如下: 00001001^00000101=00001100 (十进制为12)可见9^5=12
2、判断奇偶数
判断一个数是奇数还是偶数,一般的做法如下:
if( n % 2) == 1 // n 是个奇数 }
如果把 n 以二进制的形式展示的话,其实我们只需要判断最后一个二进制位是 1 还是 0 就行了,如果是 1 的话,代表是奇数,如果是 0 则代表是偶数,所以采用位运算的方式的话,代码如下:
if(n & 1 == 1){ // n 是个奇数。 }
例如:5以二进制表示就是:101,因此5 & 1 = 0000 0000 0000 0000 0000 0000 0000 0101 & 0000 0000 0000 0000 0000 0000 0000 0001 = 0000 0000 0000 0000 0000 0000 0000 0001转换为十进制即1,因此使用位运算结果是否为1可以判断是否奇偶数。
3、交换两个数
交换两个数的值,一般的做法是使用一个中间变量:
int tmp = x; x = y; y = tmp;
但是如果不允许使用辅助变量,则可以使用位运算实现:
x = x ^ y // (1) y = x ^ y // (2) x = x ^ y // (3)
例如:要交换 x = 5 和 y = 6,则操作步骤如下:
(1)x = x ^ y = 0000 0000 0000 0000 0000 0000 0000 0101 ^ 0000 0000 0000 0000 0000 0000 0000 0110 = 0000 0000 0000 0000 0000 0000 0000 0011 = 3
(2)y = x ^ y = 0000 0000 0000 0000 0000 0000 0000 0011 ^ 0000 0000 0000 0000 0000 0000 0000 0110 = 0000 0000 0000 0000 0000 0000 0000 0101 = 5
(3)x = x ^ y = 0000 0000 0000 0000 0000 0000 0000 0011 ^ 0000 0000 0000 0000 0000 0000 0000 0101 = 0000 0000 0000 0000 0000 0000 0000 0110 = 6
异或运算支持运算的交换律和结合律,两个相同的数异或之后结果会等于 0,即 n ^ n = 0。并且任何数与 0 异或等于它本身,即 n ^ 0 = n。所以,解释如下:
把(1)中的 x 带入 (2)中的 x,有
y = x^y = (x^y)^y = x^(y^y) = x^0 = x。 x 的值成功赋给了 y。
对于(3),推导如下:
x = x^y = (x^y)^x = (x^x)^y = 0^y = y。
4、找出没有重复的数
给你一组整型数据,这些数据中,其中有一个数只出现了一次,其他的数都出现了两次,找出出现一次的数 。
一般的解法为:会用一个哈希表来存储,每次存储的时候,记录 某个数出现的次数,最后再遍历哈希表,看看哪个数只出现了一次。这种方法的时间复杂度为 O(n),空间复杂度也为 O(n)了。
两个相同的数异或的结果是 0,一个数和 0 异或的结果是它本身,所以我们把这一组整型全部异或一下,例如这组数据是:1, 2, 3, 4, 5, 1, 2, 3, 4。其中 5 只出现了一次,其他都出现了两次,把他们全部异或一下,由于异或支持交换律和结合律,所以结果如下:
1 ^ 2 ^ 3 ^ 4 ^ 5 ^ 1 ^ 2 ^ 3 ^ 4 = (1 ^ 1) ^ ( 2 ^ 2) ^ (3 ^ 3) ^ (4 ^ 4) ^ 5 = 0 ^ 0 ^ 0 ^0 ^ 5 = 5。
也就是说,那些出现了两次的数异或之后会变成0,那个出现一次的数,和 0 异或之后就等于它本身
int find(int[] arr){ int tmp = arr[0]; for(int i = 1;i < arr.length; i++){ tmp = tmp ^ arr[i]; } return tmp; }
5、求 m 的 n 次方
求解 m 的 n 次方,并且不能使用系统自带的 pow 函数,一般方法是,连续让 n 个 m 相乘就行了:
int pow(int n){ int tmp = 1; for(int i = 1; i <= n; i++) { tmp = tmp * m; } return tmp; }
时间复杂度为 O(n),如果n比较大的话效率比较低。
使用位运算,例如 n = 13,则 n 的二进制表示为 1101, 那么 m 的 13 次方可以拆解为:
m¹¹º¹ = mººº¹ * mº¹ºº * m¹ººº。
我们可以通过 & 1和 >>1 来逐位读取 1101,为1时将该位代表的乘数累乘到最终结果。即
int pow(int n){ int sum = 1; int tmp = m; while(n != 0){ if(n & 1 == 1){ sum *= tmp; } tmp *= tmp; n = n >> 1; } return sum; }
时间复杂度近为 O(logn)
6、找出不大于N的最大的2的幂指数
传统的做法就是让 1 不断着乘以 2:
int findN(int N){ int sum = 1; while(true){ if(sum * 2 > N){ return sum; } sum = sum * 2; } }
时间复杂度是 O(logn)。
使用位运算,例如 N = 19,那么转换成二进制就是 00010011(这里为了方便,我采用8位的二进制来表示)。那么我们要找的数就是,把二进制中最左边的 1 保留,后面的 1 全部变为 0。即我们的目标数是 00010000。那么如何获得这个数呢?相应解法如下:
1、找到最左边的 1,然后把它右边的所有 0 变成 1
2、把得到的数值加 1,可以得到 00100000即 00011111 + 1 = 00100000。
3、把 得到的 00100000 向右移动一位,即可得到 00010000,即 00100000 >> 1 = 00010000。
那么问题来了,第一步中把最左边 1 中后面的 0 转化为 1 该怎么弄呢?我先给出代码再解释吧。下面这段代码就可以把最左边 1 中后面的 0 全部转化为 1
n |= n >> 1; n |= n >> 2; n |= n >> 4;
就是通过把 n 右移并且做或运算即可得到。我们假设最左边的 1 处于二进制位中的第 k 位(从左往右数),那么把 n 右移一位之后,那么得到的结果中第 k+1 位也必定为 1,然后把 n 与右移后的结果做或运算,那么得到的结果中第 k 和 第 k + 1 位必定是 1;同样的道理,再次把 n 右移两位,那么得到的结果中第 k+2和第 k+3 位必定是 1,然后再次做或运算,那么就能得到第 k, k+1, k+2, k+3 都是 1,如此往复下去….
例如:n = 19 则:
(1) n >> 1 = 00010011 >> 1 = 00001001, 因此n |= n >> 1就等于:n = 00010011 | 00001001 = 00011011
(2)n |= n >> 2 等价于:n = 0001 1011 | 0000 0110 = 0001 1111
(3)n |= n >> 4 等价于:n = 0001 1111 | 0000 0001 = 0001 1111
因此实现方式如下:
int findN(int n){ n |= n >> 1; n |= n >> 2; n |= n >> 4; n |= n >> 8; n |= n >> 16; // 整型一般是 32 位 return (n + 1) >> 1; }
时间复杂度近似 O(1)。
https://4ark.me/post/3953655a.html
九 生产环境下到底该如何部署Tomcat?
1 Tomcat组件
Tomcat请求流程:
1、对外接收请求是Connector连接器组件,可以支持不同协议,Connector组件中可设置端口,所以我们请求的时候需要输入端口号。可以把Connector当作接待员。
2、Connector组件接收到请求后,转发给处理Engine(catalina引擎)组件去处理。
3、根据请求的域名,分配到对应的Host主机。
4、在根据path分配context组件
区分项目有2个核心组件,一个是Host,一个是Context。根据域名和path分配不同的项目。其实还少了一个就是启动参数的配置,也就是不同项目的启动参数也可以不一样,如端口号,线程数啊。
推荐阅读:《让面试官颤抖的Tomcat系统架构系列!》
2 Tomcat目录结构
在一般情况下,我们要部署一个web应用,只要把应用的war包放到webapps就可以了。这时候可能会有如下问题:
如果我们要部署两个web应用Web-A和Web-B,把他放到webapps中。我们到bin目录下运行startup.sh启动,这样web-A和web-B就可以访问了。
如果现在业务上需要把web-B先暂停,那我们该怎么办?还有就是Tomcat启动是会有启动参数设置,如最大线程数,最小线程数等配置。那web-A和web-B怎么配置不一样的启动参数呢?
其实还有一个问题,如果我们要把Tomcat版本升级,怎么办?把Tomcat直接覆盖?那些web应用重新部署?
3 目录规划
Tomcat软链接
我们先把Tomcat应用放到/usr/local目录下:
上面我们是应用了Tomcat8.5版本,如果我们需要升级到9.x版本的话,那关于Tomcat目录的路径就需要重新修改,这就太不方便了,所以我们可以用软链接的方式解决这个问题
这样以后用Tomcat应用路径,就直接使用Tomcat这个软链接,即使将来Tomcat升级只要修改一些软链接就行了,其他就不需要改。
5 目录分离
我们应该要把Tomcat和web应用目录分离出来,即使Tomcat升级也跟web应用没有关系。那分离出来,怎么启动呢?
我们要利用启动参数中的CATALINA_HOME和CATALINA_BASE,来指定Tomcat程序应用和web应用;通过CATALINA_BASE就可以实现web应用分离出去,我们来看一些Tomcat一共有哪些启动参数
我们先在/usr/local目录下新建一个web-apps目录,此目录就放web应用
在web-apps目录下,新建web-a和web-b目录,这两个目录就是web-A和web-b的web应用目录。
再在web-a和web-b目录下,新建webapps和logs目录,webapps存放web应用,logs存放日志文件。
到此目录分离开了,但还缺少一个启动脚本!
6 启动脚本
此启动脚本tomcat.sh
脚本比较简单,核心就是启动参数,只要注意CATALINA_BASE="`pwd`"的意思是,执行脚本的路径,也就是代表web应用路径是脚本执行的路径;
再把tomcat.sh设置一些启动权限 # chmod +x tomcat.sh 。
修改conf下的server.xml
修改了红色字体部分,host中的appBase是相对CATALINA_BASE的路径,就是web应用的路径,context中的path是请求url,docBase也是相对路径,相对于appBase的,当然也可以设置绝对路径。在web-a下创建index.html文件
到现在为止的web-a的目录下
启动tomcat.sh
![]()
访问 http://192.168.31.150:8080/就ok了,直接返回了index.html里面的内容。
需要说明的是,在web-a执行tomcat.sh,里面的启动参数CATALINA_BASE是web应用路径,那tomcat.sh脚本中的$CATALINA_HOME/bin/catalina.sh 这个脚本执行所采用的conf配置文件是web-a目录下的,跟Tomcat程序的conf没有任务关系,也跟web-b目录下的conf也没有任何关系,这样就达到了应用之间的配置分离。
十 限流算法
对于一个分布式系统而言,如何保证系统的稳定可靠,永远都是头等大事。缓存、限流和降级是最有效也是我们最常用的手段。
由于系统资源是有限的,系统的处理能力也是有限的,对于那些已经超出系统处理能力的请求我们应该尽可能早的识别出来并让其等待或拒绝这些请求。
当大流量进入系统而我们又不进行限流,那么处理请求能力最差的一个子系统将会最先宕机,进而导致依赖这个子系统的其它系统也跟着宕机,最终导致整个系统全面瘫痪,这就是系统雪崩效应。
限流的前提是我们能够准确的计算出过去一段时间的请求数量,然后根据系统负载能力来判断接下来的请求是否放行。常用的限流算法可以分为两大类:计数法和桶算法。其中计数法又可以分为计数器和滑动窗口计数法,桶算法则分为漏桶法和令牌桶法。
1 计数器
这种限流算法是最为简单直接的了。直接记录一下当前周期内的请求个数,如果请求个数超出了阈值,那么就限制请求,如果没有超出,就放行。如下图所示:
计数器法虽然实现上非常简单,也很容易理解,但是它的缺点也是非常明显的。我们假设一种情况:
系统限流的QPS为100,第一秒有90个请求,并且所有的请求都在最后100ms进入,这个时候请求没有达到阈值,是不会限流的。紧接着第二秒也有90个请求,不过全部集中在前100ms进入,这个时候也没有达到阈值,也不会限流。然而如果我们全局分析,会发现在短短的200ms内进入了180个请求,这显然是远远超出了限流阈值100的。具体情况如下图所示:
2 滑动窗口
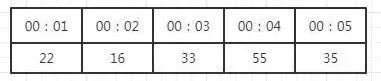
滑动窗口法是在计数器法的基础上演进而来的,也是采用计数的方式来统计过去一段时间的请求数。与计数器法不一样的地方是:滑动窗口计数会把计数窗口进行分割,比如分割成两份、10份等,分割的越小,精度越高。如下图所示:
上图展示了把统计窗口均分为10等分的情况,假设统计窗口为1秒,那么每一小格代表的就是100ms的请求计数,最近1秒中的请求总数就等于最近10小格的统计数之和。每过去100ms,统计窗口就向右滑动一小格(这就是滑动窗口法的由来),最新的数据记录在最右边位置,最左一格的数据将会被丢弃(具体实现上会有所差异)。
其实滑动窗口法并没有完全消除计数器法中遇到的问题,它只是减小了影响。假设限流QPS大小为X,窗口均分为N份,那么理论上可以达到的峰值QPS为X * (N + 1) / N,它显然是大于X的。不过我们多均分几份以后,影响就会大大减少。
3 漏桶法
漏桶法非常的简单,也非常的形象。我们可以把整个系统看成一个水桶,进来的请求理解为往桶里注入水,处理请求就是桶中的的流出。漏桶法就是不管注入水(请求进入)的快慢如何,我只按照恒定的流水出水(处理请求)。
固定线程个数的线程池就是我们平时接触的比较多的漏桶法限流的例子,这种情况中不管需要处理的任务有多少,线程池最多只会运行固定个数的任务,其余的任务要么被拒绝要么等待。
4 令牌桶算法
令牌桶算法就是系统会安装固定的速率往桶中添加令牌,请求的时候先到桶里拿一个令牌,如果能够拿到令牌就表示可以进行请求处理,如果桶里没有令牌了,就表明需要限流了。
5 常用的限流库
Google的Guava工具集中有一个RateLimiter限流器,在令牌桶的算法基础上进行改良实现的。
阿里开源的Sentinel也具有限流的功能,采用的是滑动窗口算法进行限流。
![[日常]日常学习总结一_第1张图片](http://img.e-com-net.com/image/info8/2387fcbe044b476b9d02e456e2d35ea0.jpg)
![[日常]日常学习总结一_第2张图片](http://img.e-com-net.com/image/info8/3005a14c5fd1444ebbeb8122e2236824.jpg)
![[日常]日常学习总结一_第3张图片](http://img.e-com-net.com/image/info8/2fe1d521e5cc492e9ea9b9e1c95c7e24.jpg)
![[日常]日常学习总结一_第4张图片](http://img.e-com-net.com/image/info8/d366504970374e77a3f11c241b94c67a.jpg)
![[日常]日常学习总结一_第5张图片](http://img.e-com-net.com/image/info8/39be2a12fd7c4de79d927d2b2ec1a851.png)
![[日常]日常学习总结一_第6张图片](http://img.e-com-net.com/image/info8/cd05de3f06a544ebab74157af340c3eb.png)
![[日常]日常学习总结一_第7张图片](http://img.e-com-net.com/image/info8/e2efa6bddd96455cad88b1d1144ca737.png)
![[日常]日常学习总结一_第8张图片](http://img.e-com-net.com/image/info8/3c7ddf92d9a94e00ab6d4cda1d9b965b.png)


![[日常]日常学习总结一_第9张图片](http://img.e-com-net.com/image/info8/1488f8b9752f44bfba015f6d26b80193.jpg)
![[日常]日常学习总结一_第10张图片](http://img.e-com-net.com/image/info8/b75f9fac52fe40a29fac9938b3a9a0b2.jpg)
![[日常]日常学习总结一_第11张图片](http://img.e-com-net.com/image/info8/a779f3ea59d943d2b288076a5e244505.jpg)


![[日常]日常学习总结一_第12张图片](http://img.e-com-net.com/image/info8/785b4405ced041ad9264c4c2a7cef598.jpg)

![[日常]日常学习总结一_第13张图片](http://img.e-com-net.com/image/info8/01b03b5675f84f89b53dc5673950d580.jpg)
![[日常]日常学习总结一_第14张图片](http://img.e-com-net.com/image/info8/1aa4f0848612488db55a723994566a8f.jpg)
![[日常]日常学习总结一_第15张图片](http://img.e-com-net.com/image/info8/306d06626cb54d51990bdaa8a2358cf0.jpg)
![[日常]日常学习总结一_第16张图片](http://img.e-com-net.com/image/info8/c87394e27682429f85f892f42e5a27ef.jpg)
![[日常]日常学习总结一_第17张图片](http://img.e-com-net.com/image/info8/172fa7ae477443e9a46c6b4c0079ebc8.jpg)
![[日常]日常学习总结一_第18张图片](http://img.e-com-net.com/image/info8/4708619242c34cf0b33ae171bbc113b0.jpg)
![[日常]日常学习总结一_第19张图片](http://img.e-com-net.com/image/info8/b7d801e2943e4360a3670cb8796c1ca0.jpg)
![[日常]日常学习总结一_第20张图片](http://img.e-com-net.com/image/info8/69b35c9af7b84afa8b19e38234ca06c9.jpg)