本系列博客习题来自《算法(第四版)》,算是本人的读书笔记,如果有人在读这本书的,欢迎大家多多交流。为了方便讨论,本人新建了一个微信群(算法交流),想要加入的,请添加我的微信号:zhujinhui207407 谢谢。另外,本人的个人博客 http://www.kyson.cn 也在不停的更新中,欢迎一起讨论
知识点
- 数组访问的次数计算
题目
1.5.3 使用加权 quick-union 算法(请见算法 1.5)完成练习 1.5.1 。
1.5.3 Do Exercise 1.5.1, but use weighted quick-union (page 228).
分析
weight, 要理解加权是什么意思,首先需要理解什么叫“权”,“权”的古代含义为秤砣,就是秤上可以滑动以观察质量的那个铁疙瘩。在现在,“权”又有了新的数学方面的意义,即“权重”,通俗理解就是“系数”的意思。所以“加权”的意思就是“乘以权重”,即“乘以系数”的意思。
加权quick-union 算法的代码为:
public class WeightedQuickUnionUF {
private int[] id;
private int[] sz;
private int count;
// parent link (site indexed)
// size of component for roots (site indexed)
// number of components
public WeightedQuickUnionUF(int N) {
count = N;
id = new int[N];
for (int i = 0; i < N; i++) id[i] = i;
sz = new int[N];
for (int i = 0; i < N; i++) sz[i] = 1;
}
public int count() {
return count;
}
public boolean connected(int p, int q) {
return find(p) == find(q);
}
private int find(int p) { // Follow links to find a root.
while (p != id[p]) p = id[p];
return p;
}
public void union(int p, int q) {
int i = find(p);
int j = find(q);
if (i == j) return;
// Make smaller root point to larger one.
if (sz[i] < sz[j]) {
id[i] = j;
sz[j] += sz[i];
} else {
id[j] = i;
sz[i] += sz[j];
}
count--;
}
}
将以上代码稍加改动可以写一个用于计算数组访问次数的程序,如下:
public class WeightedQuickUnionUFAccessTimes {
private int[] id;
private int[] sz;
private int count;
//数组访问次数
int eachDoUnionArrayAccessTimes = 0;
// parent link (site indexed)
// size of component for roots (site indexed)
// number of components
public WeightedQuickUnionUFAccessTimes(int N) {
count = N;
id = new int[N];
for (int i = 0; i < N; i++) id[i] = i;
sz = new int[N];
for (int i = 0; i < N; i++) sz[i] = 1;
}
public int count() {
return count;
}
public boolean connected(int p, int q) {
return find(p) == find(q);
}
private int find(int p) { // Follow links to find a root.
while (p != id[p]) {
p = id[p];
eachDoUnionArrayAccessTimes += 2;
}
eachDoUnionArrayAccessTimes++;
return p;
}
public void union(int p, int q) {
boolean printDetail = true;
if (printDetail) {
eachDoUnionArrayAccessTimes = 0;
System.out.println("开始联通分量"+p+"和"+q);
}
int i = find(p);
int j = find(q);
if (i == j) return;
// Make smaller root point to larger one.
if (sz[i] < sz[j]) {
id[i] = j;
sz[j] += sz[i];
} else {
id[j] = i;
sz[i] += sz[j];
}
count--;
eachDoUnionArrayAccessTimes++;
/************************/
if (printDetail) {
/***
* 以下代码输出数组元素
*/
System.out.print("id:{");
for (int index = 0; index < id.length; index++) {
if (index == id.length - 1) {
System.out.print(id[index]);
} else {
System.out.print(id[index] + ",");
}
}
System.out.print("}");
System.out.println("");
}
System.out.println("数组访问的次数:"+eachDoUnionArrayAccessTimes);
}
}
测试用例
public static void main(String[] args) {
WeightedQuickUnionUFAccessTimes quickUnionUF = new WeightedQuickUnionUFAccessTimes(10);
quickUnionUF.union(9,0);
quickUnionUF.union(3,4);
quickUnionUF.union(5,8);
quickUnionUF.union(7,2);
quickUnionUF.union(2,1);
quickUnionUF.union(5,7);
quickUnionUF.union(0,3);
quickUnionUF.union(4,2);
}
以上代码可以在WeightedQuickUnionUFAccessTimes.java得到
得到输出的结果为:
开始联通分量9和0
id:{9,1,2,3,4,5,6,7,8,9}
数组访问的次数:3
开始联通分量3和4
id:{9,1,2,3,3,5,6,7,8,9}
数组访问的次数:3
开始联通分量5和8
id:{9,1,2,3,3,5,6,7,5,9}
数组访问的次数:3
开始联通分量7和2
id:{9,1,7,3,3,5,6,7,5,9}
数组访问的次数:3
开始联通分量2和1
id:{9,7,7,3,3,5,6,7,5,9}
数组访问的次数:5
开始联通分量5和7
id:{9,7,7,3,3,7,6,7,5,9}
数组访问的次数:3
开始联通分量0和3
id:{9,7,7,9,3,7,6,7,5,9}
数组访问的次数:5
开始联通分量4和2
id:{9,7,7,9,3,7,6,7,5,7}
数组访问的次数:9
代码索引
WeightedQuickUnionUF.java
题目
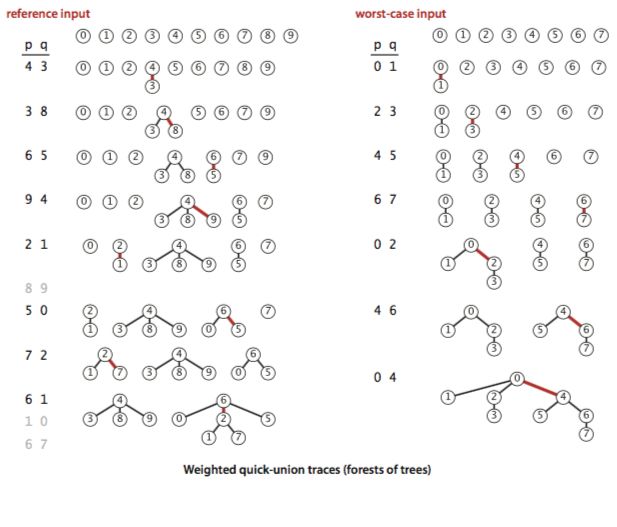
1.5.4 在正文的加权 quick-union 算法示例中,对于输入的每一对整数(包括对照输入和最坏情况下的输入),给出 id[] 和 sz[] 数组的内容以及访问数组的次数。
1.5.4 Show the contents of the sz[] and id[] arrays and the number of array accesses for each input pair corresponding to the weighted quick-union examples in the text (both the reference input and the worst-case input).
分析
加权 quick-union的算法示例如下:
为了实现题目要求,我们这里对 WeightedQuickUnionUFAccessTimes.java做个改动,一个是增加了sz数组的访问次数,一个是增加了sz每次union后的sz数组的元素,结果如下:
public class WeightedQuickUnionUFSample {
private int[] id;
private int[] sz;
private int count;
//数组访问次数
private int eachDoUnionArrayAccessTimes = 0;
private int eachDoSZArrayAccessTimes = 0;
// parent link (site indexed)
// size of component for roots (site indexed)
// number of components
public WeightedQuickUnionUFSample(int N) {
count = N;
id = new int[N];
for (int i = 0; i < N; i++) id[i] = i;
sz = new int[N];
for (int i = 0; i < N; i++) sz[i] = 1;
}
public int count() {
return count;
}
public boolean connected(int p, int q) {
return find(p) == find(q);
}
private int find(int p) { // Follow links to find a root.
while (p != id[p]) {
p = id[p];
eachDoUnionArrayAccessTimes += 2;
}
eachDoUnionArrayAccessTimes++;
return p;
}
public void union(int p, int q) {
boolean printDetail = true;
if (printDetail) {
eachDoUnionArrayAccessTimes = 0;
eachDoSZArrayAccessTimes = 0;
System.out.println("开始联通分量"+p+"和"+q);
}
int i = find(p);
int j = find(q);
if (i == j) return;
// Make smaller root point to larger one.
if (sz[i] < sz[j]) {
id[i] = j;
sz[j] += sz[i];
} else {
id[j] = i;
sz[i] += sz[j];
}
count--;
eachDoUnionArrayAccessTimes++;
eachDoSZArrayAccessTimes += 4;
/************************/
if (printDetail) {
/***
* 以下代码输出数组元素
*/
System.out.print("id:{");
for (int index = 0; index < id.length; index++) {
if (index == id.length - 1) {
System.out.print(id[index]);
} else {
System.out.print(id[index] + ",");
}
}
System.out.print("}");
System.out.println("");
/**
* 输出sz
*/
System.out.print("sz:{");
for (int index = 0; index < sz.length; index++) {
if (index == sz.length - 1) {
System.out.print(sz[index]);
} else {
System.out.print(sz[index] + ",");
}
}
System.out.print("}");
System.out.println("");
}
System.out.println("数组id访问的次数:"+ eachDoUnionArrayAccessTimes);
System.out.println("数组sz访问的次数:"+ eachDoSZArrayAccessTimes);
}
public static void main(String[] args){
WeightedQuickUnionUFSample sample = new WeightedQuickUnionUFSample(10);
sample.union(4,3);
sample.union(3,8);
sample.union(6,5);
sample.union(9,4);
sample.union(2,1);
sample.union(5,0);
sample.union(7,2);
sample.union(6,1);
}
}
将书中的实例数据调用后的结果如下:
开始联通分量4和3
id:{0,1,2,4,4,5,6,7,8,9}
sz:{1,1,1,1,2,1,1,1,1,1}
数组id访问的次数:3
数组sz访问的次数:4
开始联通分量3和8
id:{0,1,2,4,4,5,6,7,4,9}
sz:{1,1,1,1,3,1,1,1,1,1}
数组id访问的次数:5
数组sz访问的次数:4
开始联通分量6和5
id:{0,1,2,4,4,6,6,7,4,9}
sz:{1,1,1,1,3,1,2,1,1,1}
数组id访问的次数:3
数组sz访问的次数:4
开始联通分量9和4
id:{0,1,2,4,4,6,6,7,4,4}
sz:{1,1,1,1,4,1,2,1,1,1}
数组id访问的次数:3
数组sz访问的次数:4
开始联通分量2和1
id:{0,2,2,4,4,6,6,7,4,4}
sz:{1,1,2,1,4,1,2,1,1,1}
数组id访问的次数:3
数组sz访问的次数:4
开始联通分量5和0
id:{6,2,2,4,4,6,6,7,4,4}
sz:{1,1,2,1,4,1,3,1,1,1}
数组id访问的次数:5
数组sz访问的次数:4
开始联通分量7和2
id:{6,2,2,4,4,6,6,2,4,4}
sz:{1,1,3,1,4,1,3,1,1,1}
数组id访问的次数:3
数组sz访问的次数:4
开始联通分量6和1
id:{6,2,6,4,4,6,6,2,4,4}
sz:{1,1,3,1,4,1,6,1,1,1}
数组id访问的次数:5
数组sz访问的次数:4
答案
见分析
代码索引
WeightedQuickUnionUFSample.java