李光证 3117004660
吴子昊 3117004671
李光证博文地址:https://www.cnblogs.com/Gleez/p/11688368.html
一、
1. github项目地址:
https://github.com/amekao/SE_work2
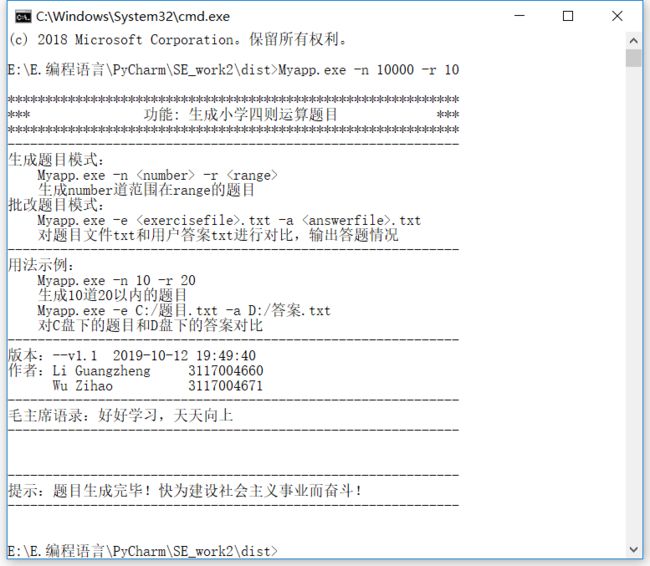
2. 界面示例:
生成模式
批改模式
二、PSP表格
| PSP2.1 |
Personal Software Process Stages |
预估耗时(分钟) |
实际耗时(分钟) |
| Planning |
计划 |
|
|
| · Estimate |
· 估计这个任务需要多少时间 |
1200 |
1200 |
| Development |
开发 |
|
|
| · Analysis |
· 需求分析 (包括学习新技术) |
180 |
200 |
| · Design Spec |
· 生成设计文档 |
20 |
30 |
| · Design Review |
· 设计复审 (和同事审核设计文档) |
30 |
60 |
| · Coding Standard |
· 代码规范 (为目前的开发制定合适的规范) |
30 |
30 |
| · Design |
· 具体设计 |
100 |
100 |
| · Coding |
· 具体编码 |
600 |
720 |
| · Code Review |
· 代码复审 |
200 |
180 |
| · Test |
· 测试(自我测试,修改代码,提交修改) |
100 |
90 |
| Reporting |
报告 |
|
|
| · Test Report |
· 测试报告 |
30 |
40 |
| · Size Measurement |
· 计算工作量 |
10 |
10 |
| · Postmortem & Process Improvement Plan |
· 事后总结, 并提出过程改进计划 |
10 |
10 |
| 合计 |
|
1310 |
1470 |
三、效能分析
使用line_profiler模块对时间进行测试:
①重新写了一个time.py进行测试,对里面main函数修改,不使用argv来获取参数,而是直接在程序里面赋值
②在需要测试的模块前加上@profiler标志符
③使用 kernprof -l time.py运行程序,生成time.py.lprof报表
④使用 python -m line_profiler time.py.lprof 查看报表
生成模式:生成10000道范围在0到10的题目
生成模式核心代码:
# 生成模式 ques_count = 10000 max_val = 10 random_exercises(ques_count, max_val)
核心模块random_exercises的用时:
Total time: 5.14441 s File: time.py Function: random_exercises at line 12 Line # Hits Time Per Hit % Time Line Contents ============================================================== 12 @profile 13 def random_exercises(q_c, m_v): 14 """ 15 根据输入的题目数量和数字范围,生成题目文件和答案文件 16 :param q_c: 题目数量 17 :param m_v: 数字最大值 18 :return: 在目录下生成试题文件和答案文件 19 """ 20 1 1028.0 1028.0 0.0 e_open = open("Exercises.txt", "a+") 21 1 1073.0 1073.0 0.0 a_open = open("Answers.txt", "a+") 22 10001 14619.0 1.5 0.1 for i in range(0, q_c): 23 10000 7059101.0 705.9 56.3 post = question.post_order_generator(m_v) 24 10000 217674.0 21.8 1.7 tree = question.post_to_tree(post) 25 10000 178163.0 17.8 1.4 ordinary = question.tree_to_ordinary(tree, []) 26 10000 2002280.0 200.2 16.0 readable_str = question.to_readable(ordinary) 27 10000 109711.0 11.0 0.9 e_open.write(f'{i+1}、{readable_str}\n') 28 29 10000 2428198.0 242.8 19.4 ans = question.count_ans(post) 30 10000 423654.0 42.4 3.4 answer = question.to_with_fraction(ans) # 转成带分数 31 10000 103062.0 10.3 0.8 a_open.write(f'{i+1}、{answer}\n') 32 1 576.0 576.0 0.0 e_open.close() 33 1 390.0 390.0 0.0 a_open.close()
批改模式:对刚才生成的10000条题目的答案进行修改
批改模式核心代码:
# 批改模式 exercise_path = "Exercises.txt" answer_path = "Answers.txt" make_standard(exercise_path) check_exercise(answer_path)
模块make_standard的用时:
Total time: 1.72545 s File: time.py Function: make_standard at line 35 Line # Hits Time Per Hit % Time Line Contents ============================================================== 35 @profile 36 def make_standard(e_p): 37 """ 38 根据题目文件生成标准答案StandardAnswers.txt 39 :param e_p: 题目文件的path 40 :return: 生成StandardAnswers.txt 41 """ 42 1 9.0 9.0 0.0 try: 43 1 409.0 409.0 0.0 e_open = open(e_p, "r") 44 except FileNotFoundError: 45 print("找不到该文件") 46 sys.exit() 47 except: 48 print("文件打开失败,请重新运行程序") 49 sys.exit() 50 1 775.0 775.0 0.0 sa_open = open("StandardAnswers.txt", "a+") 51 1 10663.0 10663.0 0.3 e_lines = e_open.readlines() 52 10001 15022.0 1.5 0.4 for line in e_lines: 53 10000 28078.0 2.8 0.7 ques_num = line.split("、")[0] # 题目序号 54 10000 31358.0 3.1 0.7 ques_str = line.split("、")[1].rstrip('\n') # 去掉前面的序号和后面换行符 55 10000 894383.0 89.4 21.3 ordinary = question.to_unreadable(ques_str) 56 10000 370173.0 37.0 8.8 post = question.ordinary_to_post(ordinary) 57 10000 2341848.0 234.2 55.7 sa = question.count_ans(post) 58 10000 413446.0 41.3 9.8 standard = question.to_with_fraction(sa) 59 10000 98687.0 9.9 2.3 sa_open.write(f'{ques_num}、{standard}\n') 60 61 1 266.0 266.0 0.0 e_open.close() 62 1 673.0 673.0 0.0 sa_open.close()
模块check_exercises的用时:
Total time: 0.0277891 s File: time.py Function: check_exercise at line 64 Line # Hits Time Per Hit % Time Line Contents ============================================================== 64 @profile 65 def check_exercise(a_p): 66 """ 67 标准答案与用户答案逐行对比,统计对错 68 :param a_p: 用户答案path 69 :return: 生成Grade.txt统计文件 70 """ 71 1 459.0 459.0 0.7 sa_open = open("StandardAnswers.txt", "r") 72 1 264.0 264.0 0.4 a_open = open(a_p, "r") 73 1 5800.0 5800.0 8.6 sa_lines = sa_open.readlines() 74 1 3.0 3.0 0.0 right = [] 75 1 1.0 1.0 0.0 wrong = [] 76 77 10001 10571.0 1.1 15.6 for sa_line in sa_lines: 78 10000 20640.0 2.1 30.5 if sa_line == a_open.readline(): 79 10000 20990.0 2.1 31.0 right.append(sa_line.split("、")[0]) 80 else: 81 wrong.append(sa_line.split("、")[0]) 82 1 94.0 94.0 0.1 sa_open.close() 83 1 32.0 32.0 0.0 a_open.close() 84 85 1 5839.0 5839.0 8.6 grade_open = open("Grade.txt", "a+") 86 1 3019.0 3019.0 4.5 grade_open.write(f'正确{len(right)}题:{right}\n') 87 1 24.0 24.0 0.0 grade_open.write(f'错误{len(wrong)}题:{wrong}\n')
具体时间分析看第五部分后面
四、设计实现过程
简易版类图
question.py是与数学操作相关的函数,大部分由光证同学完成
main.py是主函数,负责获取用户输入并调用question里面函数,由子昊同学完成
程序有正向输出和逆向两部分模块
正向输出:逆波兰表达式列表 → 转化为二叉树 → 转化为中序表达式列表 → 转化为人看的字符串形式
逆向:人看的字符串形式 → 中序表达式列表 → 逆波兰表达式列表
逆波兰表达式的好处是不需要括号,减少程序复杂度,运算顺序完全取决于数字的排列,而且计算可以方便地通过入栈出栈来实现。
生成题目模式使用的random_exercises模块就是正向输出,先生成逆波兰表达式,使用count_ans函数进行计算,存入Answers.txt中,之后再正向输出字符串到Exercises.txt
批改题目模式使用make_standard模块:逆向把Exercises.txt的字符串转化为逆波兰表达式,使用count_ans函数进行计算,保存到StandardAnswers.txt
check_exercises模块:逐行与Answers.txt对比,正确的就存入right列表,错误的就存入wrong列表,最后输出各列表的元素和元素个数
五、核心代码讲解
1. 随机生成逆波兰表达式
1 def post_order_generator(max_value): 2 """ 3 逆波兰式子生成器,随机生成一个逆波兰表达式 4 :param max_value: int类型,表示数值的最大值 5 :return: 存储逆波兰表达式的列表 6 """ 7 ch = ('+', '-', '×', '÷') 8 char_num = random.randrange(1, 4) 9 num_num = char_num - 1 10 # suffix_list是逆波兰表达式列表,先在列表前面插入两个数字 11 suffix_list = [str(get_random_fraction(max_value)), str(get_random_fraction(max_value))] 12 now_num = 2 13 while char_num or num_num: 14 if now_num >= 2: 15 if char_num and random.randrange(0, 2): 16 suffix_list.append(ch[random.randrange(0, 4)]) 17 now_num = now_num - 1 18 char_num = char_num - 1 19 elif num_num: 20 suffix_list.append(str(get_random_fraction(max_value))) 21 num_num = num_num - 1 22 now_num = now_num + 1 23 else: 24 suffix_list.append(ch[random.randrange(0, 4)]) 25 char_num = char_num - 1 26 now_num = now_num - 1 27 else: 28 suffix_list.append(str(get_random_fraction(max_value))) 29 now_num = now_num + 1 30 num_num = num_num - 1 31 st = ".".join(suffix_list) 32 if st in problem_set or count_ans(suffix_list) < 0: 33 suffix_list = post_order_generator(max_value) 34 return suffix_list 35 else: 36 problem_set.add(st) 37 return suffix_list
逆波兰表达式的限制是第一二个元素必须是数字,最后一个元素必须是运算符,另外数字个数是运算符个数+1
本模块是先随机出式子有n个运算符,则数字有n+1个,除去前两个数先放入列表,和列表最后的运算符,则剩下的符号数和数字数都是n-1,之后在剩下位置随机生成
另外将生成的逆波兰表达式转化为字符串存入一个set集合中,由于集合的唯一性,如果新生成的表达式已经在集合中,则这条式子要重新生成
遗憾的是3+4和4+3的判重我们还是没有成功实现
2. 逆波兰转二叉树
1 def post_to_tree(post_list): 2 """ 3 把逆波兰式转换成一棵模拟二叉树 4 :param post_list: 逆波兰式列表 5 :return: 一个列表,表示一棵树 6 """ 7 ch = ('+', '-', '×', '÷') 8 temp = [] 9 for v in post_list: 10 if v in ch: 11 t1, t2 = temp.pop(), temp.pop() 12 temp.append([t2, t1, v]) 13 else: 14 temp.append(v) 15 return temp[0]
逆波兰表达式的两个数字存入叶子结点,运算符存入根结点,成为一棵二叉树
3. 二叉树转中序表达式
1 def tree_to_ordinary(tree_list, medium_list): 2 """ 3 把二叉树转换成普通表达式 4 :param tree_list: 二叉树的列表 5 :param medium_list:中序表达式的列表,主要为了递归调用,刚开始可传一个空列表 6 :return:一个普通表达式的列表 7 """ 8 ch_val = {'+': 1, '-': 1, '×': 2, '÷': 2} # 符号优先级 9 if type(tree_list[0]) == list: 10 if ch_val[tree_list[2]] > ch_val[tree_list[0][2]]: 11 medium_list.append('(') 12 medium_list = tree_to_ordinary(tree_list[0], medium_list) 13 medium_list.append(')') 14 else: 15 medium_list = tree_to_ordinary(tree_list[0], medium_list) 16 else: 17 medium_list.append(tree_list[0]) 18 medium_list.append(tree_list[2]) 19 if type(tree_list[1]) == list: 20 medium_list.append('(') 21 medium_list = tree_to_ordinary(tree_list[1], medium_list) 22 medium_list.append(')') 23 else: 24 medium_list.append(tree_list[1]) 25 return medium_list
对于这一棵二叉树,后序遍历就是逆波兰表达式(后缀表达式),中序遍历就是中序表达式(平时用的样式)
难点在于× ÷号的优先级比+ -号要高,遇到这种情况需要加括号
4. 计算逆波兰表达式
1 def count_ans(post_list): 2 """ 3 计算逆波兰式的结果和判断这条式子是否合法, 4 如果中途出现负数或者除零都会返回-1,否则返回最终结果 5 :param post_list: 逆波兰式的列表 6 :return: Fraction类型的结果 7 """ 8 ch = ('+', '-', '×', '÷') 9 stack = [] 10 for v in post_list: 11 if v in ch: 12 t1, t2 = stack.pop(), stack.pop() 13 try: 14 if v == '+': 15 t1 = t1 + t2 16 elif v == '-': 17 t1 = t2 - t1 18 elif v == '×': 19 t1 = t1 * t2 20 else: 21 t1 = t2 / t1 22 if t1 < 0: 23 return -1 24 stack.append(t1) 25 except ZeroDivisionError: 26 return -1 27 else: 28 stack.append(Fraction(v)) 29 return stack[0]
使用逆波兰表达式的计算就是因为式子中没有括号所以容易写程序,
将逆波兰表达式列表当做栈来使用,
新建一个ch元祖存+ - x ÷四个运算符,然后对逆波兰式列表中元素逐个遍历,如果元素是运算符,则把运算符前两个元素出栈进行计算再入栈,直到栈中没有运算符为止
回看效能分析:
生成模式:
1. 可以看到随机生成逆波兰表达式post_order_generator是最耗费时间的,占了56%的时间,猜测是因为random函数比较耗时,而一条式子平均需要5次random
2. 第二耗时间的是计算逆波兰count_ans,因为每一个列表元素都要遍历一下看在不在ch元祖里面,而且要做乘除法
3. 第三耗时间的让人惊奇,居然是转成可阅读to_readable,可能是将假分数转化为带分数需要做除法
批改模式:
1. make_standard模块中第一耗时是计算函数count_ans,理由同上
2. make_standard模块中第二耗时是转成不可阅读to_unreadable,作为to_readable的反函数,理由也是因为需要做乘法通分把整数部分加回去分子中
3. check_exercises模块中最耗时是逐行对比部分,该部分是这个模块最核心的代码,而且因为需要字符串匹配,看两边字符串是否一样
六、测试用例
由于本程序的特殊性,运行一次就可以生成n条测试,极大方便我们判断对错,以下给出生成15条算式时的例子
Myapp.exe -n 15 -r 10
生成的Exercises.txt
1、4'1/2 - 2/5 2、3/4 × 1/2 3、2'2/3 ÷ 1/2 + 1 4、2 × 4'1/2 ÷ 1'2/5 5、2/3 - ( 1/7 - ( 0 × 1'1/7 ) ) 6、5/9 ÷ 5 7、0 × 7/9 8、2 + 1'3/4 9、1'1/5 ÷ 1 10、7/9 ÷ 1 11、1 + 1'1/2 + 4 12、0 × 0 × 7/8 13、( 5/7 + 1'1/5 ) ÷ 1/4 14、4 × 3 15、1'1/7 × ( 0 + 1/3 )
生成的答案Answers.txt
1、4'1/10 2、3/8 3、6'1/3 4、6'3/7 5、11/21 6、1/9 7、0 8、3'3/4 9、1'1/5 10、7/9 11、6'1/2 12、0 13、7'23/35 14、12 15、8/21
对其中的2 3 5 7 11 13题故意改成错误答案,存为MyAnswers.txt
1、4'1/10 2、3/9 3、6'1/4 4、6'3/7 5、 6、1/9 7、5 8、3'3/4 9、1'1/5 10、7/9 11、6 12、0 13、7'23/36 14、12 15、8/21
使用如下代码执行批改模式
Myapp.exe -e Exercises.txt -a MyAnswers.txt
生成的标准答案StandardAnswers.txt和原来的Answers.txt完全一致
1、4'1/10 2、3/8 3、6'1/3 4、6'3/7 5、11/21 6、1/9 7、0 8、3'3/4 9、1'1/5 10、7/9 11、6'1/2 12、0 13、7'23/35 14、12 15、8/21
批改结果Grade.txt也判断正确
正确9题:['1', '4', '6', '8', '9', '10', '12', '14', '15'] 错误6题:['2', '3', '5', '7', '11', '13']
七、小结
1. 子昊对光证的
个人认为本次结对编程项目非常成功,大家都发挥了各自的所长,李光证同学是ACM队的,对算法比较熟悉,我因为在工作室做过项目,对使用python比较有经验
一开始我们讨论了两种方案,方案一是由内往外生成,即5 x(6 +(7 + 5)),从7+5开始生成,7+5和5+7等价,再到6+12和12+6等价,不过这样会引入很多无用的括号而且括号括的位置也千奇百怪;
因此后来选择了使用逆波兰表达式的方案,计算可以直接对列表出栈入栈,也省却了括号的麻烦,使用树即可把逆波兰表达式转为平常的中序表达式。
光证对算法方面比较熟悉,所以负责逆波兰表达式的生成,计算,转化,其他零散的部分则由我完成。
这次是光证先写出他的部分,(他花了大概5小时)再由我来组装,我在刚接手光证代码时,被一堆奇奇怪怪的数据结构方面的用法搞懵了,完全看不懂·,而且代码很乱,不符合PEP8规范,在Pycharm中全是波浪线看着很难受,所以花了一点时间教会了光证用pycharm的自动pep8,并使用‘’‘’‘’来注释函数功能,这样在悬停时就可以看到这个函数究竟是做什么的,不过光证的150多行代码还是花了一个多小时才完全看懂。
后来就是根据自己的理解把光证的函数封装好,用时大约6小时,程序就写完了,后面再用了约2个小时对框架进行优化,将模块分得更细,更容易维护。所以整个开发流程还是比较舒服的,比个人项目快了好多,表扬光证。
所以这次的成功合作,一是分工明确,光证负责数学函数,我负责封装; 二是接口定义好,相对比较独立; 三是我和光证python水平差不多,而且在同一个宿舍方便交流; 四是大家都很好完成了自己的任务,没有互相拖沓。
希望以后还有更多类似这样完美的合作。
2. 光证对子昊的
经过多天的努力,本次的结对编程项目完美结束,在这次的结对项目中,收益匪浅。
子昊在工作室里面做过项目,有过合作的经验,并且对python的使用有经验,而我是学校ACM集训队的一员,对于算法的设计、实现比较熟悉。所以我主要负责编写关于表达式的生成,转换还有计算和分数之间的转换等功能函数,而子昊负责把我写的函数整合在一起,对于输入输出的编写还有程序的性能分析。
因为我是参加ACM竞赛的,平时敲的变量名能有多短就写多短,所以这次写代码的时候也奇奇怪怪的,所以第一次给子昊的时候他很难理解,然后子昊就来给我讲了python代码的规范,还有教会了我使用pycharm的一些窍门,我改完之后就好了很多。这可能就像萧伯纳所说的那样“你有一个苹果,我有一个苹果,我们交换一下,一人还是只有一个苹果;你有一个思想,我有一个思想,我们交换一下,一人就有两个思想”。
而本次也有许多的不足之处,比如表达式重复的问题我只排除了后缀表达式相同的情况而已,还有的就是最后函数没有封装进类里面。