计算机图形学——裁剪

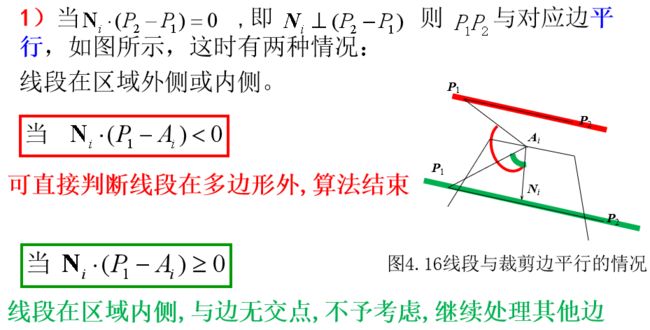
裁剪作用：
选择显示的内容--图形在窗口内的部分被显示出来，窗口外的部分被裁剪掉
 图形中每个图形基本元素都要经过裁剪，因此裁剪直接影响整个图形系统的效率。

裁剪窗口：矩形，凸多边形，任意多边形
裁剪类型：二维裁剪、三维裁剪
裁剪对象：直线段、多边形、文字等
裁剪方法:
直线的裁剪方法: Sutherland-Cohen算法 , Cyrus-Beck算法,梁友栋-Barsky算法
多边形的裁剪方法:Sutherland-Hodgman算法
三维的裁剪方法: Sutherland-Cohen算法 ,梁友栋-Barsky算法
 

一、Sutherland-Cohen算法

本算法又称为编码裁剪算法

Sutherland–Cohen算法分成两部分：

 

第一步，判定：
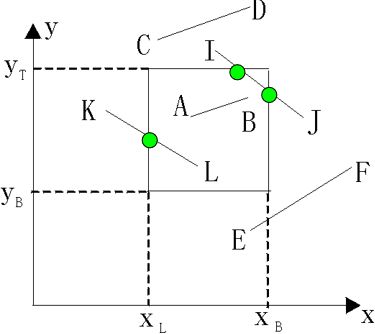
1) 完全在窗口内的直线段，称为完全可见的线段，如AB。保留着
2) 完全在窗口外的线段，称为完全不可见线段，如CD。抛弃掉

第二步，处理不能断定为完全可见或完全不可见的线段，如IJ、KL
*这时需要计算出直线段和窗口边界的一个交点，这个交点把直线分成两段，其中一条为完全不可见的线段,被抛弃。
*对余下部分再作第一步的判断，重复上述过程，直到直线段余下的部分可用第一步的判断得出肯定的结论为止。

1、判断完全可见/不可见的线段

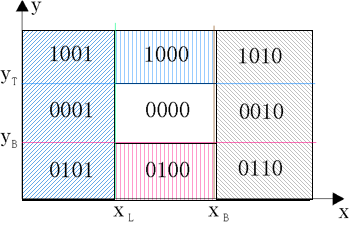
为使计算机能够快速判断一条直线段与窗口属何种关系，采用如下编码方法。窗口的四条边把整个平面分成九个区域，每一个区域采用四位编码表示：

在x=xL左侧的区域,编码的第四位是1；
在x=xR右侧的区域,编码的第三位是1；
在y=yB下侧的区域,编码的第二位是1；
在y=yT上侧的区域,编码的第一位是1。

 

如何判断？
对要被裁剪的线段的两个端点进行区域编码。

如果其所在的区域的编码均是0000（相与），则这条线段完全可见；
如果两个编码的逻辑与不为0000，则这条线段完全不可见

2、处理不能断定为完全可见或完全不可见的线段

线段KL为例，从K点(1001)的编码分析出K在x=xL的左侧，KL必和x=xL有交点，求出其交点M，KM显然是完全不可见的，因而只要对ML从第一步开始重复上述处理步骤。
由于ML还是不能用第一步下结论，又从M的编码发现M在y=yT的上侧，因而要求ML和y=yT的交点N。

丢掉MN，对NL用第一步的方法可断定NL为完全可见，至此裁剪结束。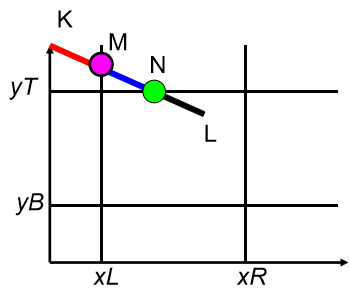

 

3、程序代码

float xl, xr, yt, yb;
unsigned char code(float x, float y) { unsigned char c = 0; if (x < xl) c = c|1; //按位或 else if (x > xr) c = c|2; if (y < yb) c = c|4; else if (y > yt) c = c|8; return c; }//给九个区域编码   void clip(float x0, float y0, float x2, float y2) { unsigned char c1, c2, c; float x, y, wx, wy; c1 = code(x0, y0); c2 = code(x2, y2); while ((!(c1 == 0)) || (!(c2 == 0))) { if ((c1& c2)) return; //两端点逻辑与不为0，则在区域外，裁去 c = c1; if (c == 0) c = c2; wx=x2-x0; wy=y2-y0; if ((c & 1) == 1) { y = y0 + wy * (xl - x0) /wx; x = xl; }//端点在xl左侧，求与xl的交点 else if ((c & 2) == 2) { y = y0 +wy * (xr - x0) /wx; x = xr; } //端点在xr右侧，求与xr的交点 else if ((c & 4) == 4) { x = x0 +wx * (yb - y0) /wy; y = yb; } //端点在yb下方，求与yb的交点 else if ((c & 8) == 8) { x = x0 +wx * (yt - y0) / wy; y = yt; } //端点在yt上方，求与yt的交点 if (c == c1) { x0 = x; y0 = y; c1 = code(x0, y0); } else { x2 = x; y2 = y; c2 = code(x2, y2); } //用交点代替端点，再返回第一步 }// While() glLine(int(x0), int(y0), int(x2), int(y2)); }

4、小结

Cohen-Sutherland裁剪算法对不与边框相交的线段进行裁剪时效率较高,而对与窗口边界有交点的线段裁剪效率低。

因而比较适合两种情况的裁剪：一是大部分线段完全可见；二是大部分线段完全不可见。

而且很多的时候,被裁剪线段仅与窗口边界延长线相交,求交点到最后是无效的操作,因为线段可能完全被丢弃;并且被裁剪线段与窗口边界相交时交点的取得比较复杂。

比如像下图这样的裁剪，这条红色线段完全是在裁剪窗口的外部，却需要进行算法计算，最后线段完全被丢弃！

 

二、中点分隔算法

中点分隔算法是对Sutherland-Cohen算法在求交点方面的改进。

核心思想是通过二分逼近来确定直线段与 窗口的交点。

取线段的中点

1、若中点不在窗口内， 则把中点和离窗口边界最远点构成的线段丢掉，以线段上的另一点和该中点再构成线段求其中点

2、如中点在窗口内，则又以中点和最远点构成线段， 并求其中点，直到中点与窗口边界的 坐标值在规定的误差范围内相等

 

重复上述过程，直到线段长度小于给定的小数ε为止。
在显示时ε可取成一个象素的宽度，对分辨率为2^N×2^N的显示器来说，上面讲的二分的过程最多只要作N次。

三、Cyrus-Beck算法

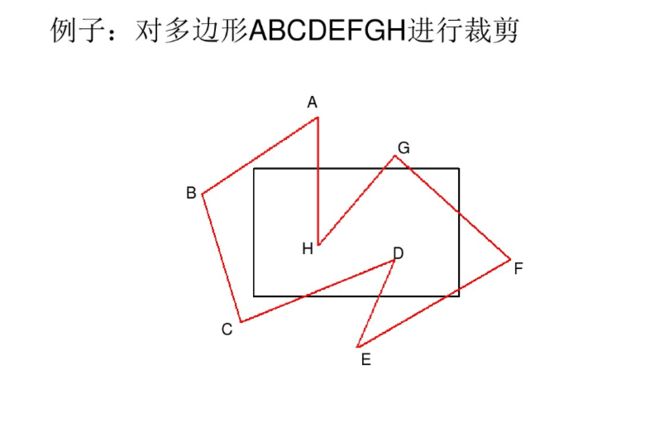
Cyrus-Beck算法可以处理任意凸多边形对线段的裁剪。

1、裁剪目标

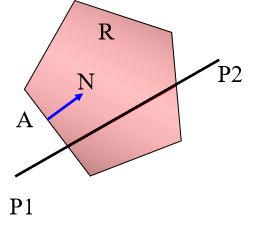
考虑如图所示一个凸多边形区域R和一条线段P1P2，要求计算线段落在区域R中的部分。

 

2、线段表示

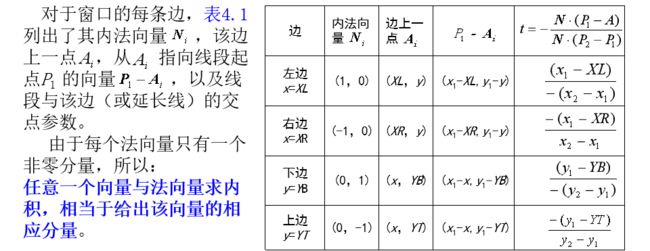
假定A是区域R边界L上一点；N是区域边界在A点的内法向量；线段P1P2用参数方程表示：

3、基本思想

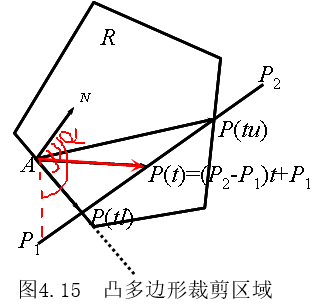
对于线段P1P2的参数方程表示，如果能判断出线段进入多边形时候的参数ts和线段退出多边形时的参数te，则tste之间的线段为裁剪完毕后的结果。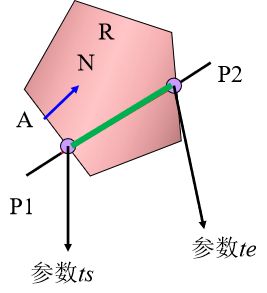

 

4、判定线段上的点和多边形的关系

假定A为区域边界L上的任意一点，记L的内法向量（垂直）为N对于线段上任意一点 Pi， Pi和多边形边界L的关系有三种可能(t 为此点的参数值)：

 

 

 

 

性质（1）: 如果点P(t)在多边形所有边的内侧，则称P是在多边形的内侧。

可见线段的参数区间

 

 

 

 

 

 

5、编程思路

 

 

6、程序代码

double ts,te;
int Cyrus_Beck (int k,double A[][2],double N[][2],double x[2],double y[2],double *ts,double *te) { int i,j; double t,dn,nw,D[2],W[2]; *ts=0; *te=1; for(i=0; i) { dn=N[i][0]*(x[1]- x[0])+N[i][1]* (y[1]-y[0]); nw=N[i][0]* (x[0]-A[i][0])+N[i][1]* (y[0]- A[i][1]); if(fabs(dn)<1.0e-6) //平行  { if(nw<0) return 0; //p在L外侧  } else { t=-nw/dn; if(dn<0) { if(t< *te) *te=t; //终点  } else if(t> *ts) *ts=t; //起点  } if(*ts>*te) return 0; //在区域外  } return 1; }

 

三、梁友栋-Barsky算法

 当凸多边形是矩形窗口，且矩形的边平行于坐标轴时， Cyrus-Beck算法可简化为梁友栋-Barsky算法。

 

 

 

 

 

基本步骤

初始化线段在边界内的端点参数为ts=0、te=1。

计算出各个裁剪边界的r、s值。

当r=0且s<0时，舍弃该线段；否则计算线段与边界的交点参数t。
当r<0时，参数t用于更新ts；
当r>0时，参数t用于更新te。

如果更新了ts或te后，使ts>te，则舍弃该线段。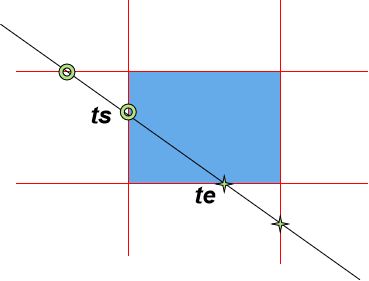

 

 

程序代码

double ts,te;
double xL,xR,yB,yT;
bool visible=false; void Liang_Barsky (double x[2],double y[2],double *ts,double *te) { double dx,dy; visible=false; dx=x[1]-x[0]; dy= y[1]-y[0]; *ts=0; *te=1; if(clipt(-dx,x[0]-xL,ts,te)) if(clipt(dx,xR-x[0],ts,te)) if(clipt(-dy,y[0]-yB,ts,te)) if(clipt(dy,yT-y[0],ts,te)) visible=true; } bool clipt (double r,double s,double * ts,double *te) { double t; if(r<0) { t=s/r; if(t>* te) return false; else if(t>* ts) *ts=t; } //起点组 else if(r>0) { t=s/r; if(t<*ts) return false; else if(t<* te) *te=t; } //终点组 else if(s<0) return false; //r=0且s<0则完全不可见 return true; }

梁友栋-Barsky算法比Sutherland-Cohen算法更有效,因为需要计算的交点数目减少了。更新参数仅仅需要一次除法,线段与窗口的交点只计算一次就计算出 ts、te的最后的值。而对于Sutherland-Cohen算法,即使一条线段完全落在裁剪窗口之外,也要对其反复求交点,而且每次求交都需要除法和乘法运算。

https://www.cnblogs.com/cnblog-wuran/p/9813841.html

四、Sutherland-Hodgman多边形裁剪

该算法的基本思想是将多边形边界作为一个整体，每次用窗口的一条边对要裁剪的多边形和中间结果多边形进行裁剪，体现一种分而治之的思想

基本原理

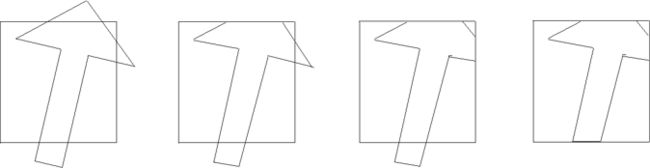
只要对多边形用窗口的四条边依次裁剪四次便可得到裁剪后的多边形。
每次用窗口的一条边界（包括延长线）对要裁剪的多边形进行裁剪，裁剪时顺序地测试多边形各顶点，保留边界内侧的顶点，删除外侧的顶点，同时，适时地插入新的顶点(即交点和窗口顶点)，从而得到一个新的多边形顶点序列。
然后以此新的顶点序列作为输入，相对第二条窗边界线进行裁剪，又得到一个更新的多边形顶点序列。
依次下去，相对于第三条、第四条边界线进行裁剪，最后输出的多边形顶点序列即为所求的裁剪好了的多边形。如下图所示。

 

 

 

 算法的输入是以顶点序列表示的多边形，输出也是一个顶点序列，构成一个或多个多边形。

考虑以窗口的一条边以及延长线构成的裁剪线，该线把平面分成两部分：一部分包含窗口，称为可见侧；另一部分称为不可见侧。

每条线段端点S、P与裁剪线比较后可输出0至2个顶点。
S、P都在可见一侧，则输出P。
S、P都在不可见一侧，则输出0个顶点。
S在可见一侧，P在不可见一侧，则输出SP与裁剪线的交点I。
S在不可见一侧，P在可见一侧，则输出SP与裁剪线的交点I和P。

 

五、字符裁剪

字符裁剪的策略有以下三种:
串精度裁剪

字符串完全落入窗口之内时才显示，否则不显示，裁剪结果如图(b)所示。其思想是求出字符串的包围盒，比较包围盒的边界极值与窗口的边界极值，若包围盒完全落于窗口之内，则显示字符串，否则不显示。

字符精度裁剪

当一个字符完全包含于窗口内时，显示该字符，否则不显示。可先用字符串包围盒判断应该完全、部分还是不显示字符串，对部分显示的字符串，再用每个字符的包围盒判断该字符是不是应该显示。裁剪结果如图(c)所示。

基于构成字符最小元素的裁剪

这种策略最为精确，即使字符只有一部分在窗口内，也要把这一部分显示出来。对点阵字符来说，构成字符的最小元素为像素，此时字符的裁剪转化为点裁剪；对矢量字符来说，构成字符的最小元素是曲线段，字符的裁剪转化为曲线的裁剪。裁剪结果如图(d)所示。