知识清单:
- t分布(t-distribution)
- 自由度(degree of freedom,df)
- 单样本t检验(one sample/group t-test)
- 配对样本t检验(paired/matched t-test)
- 两样本t检验(two-sample/group t-test)
- 正态性检验(normality test)
- 方差齐性检验(homogeneity of variance test)
- 变量变换效果展示
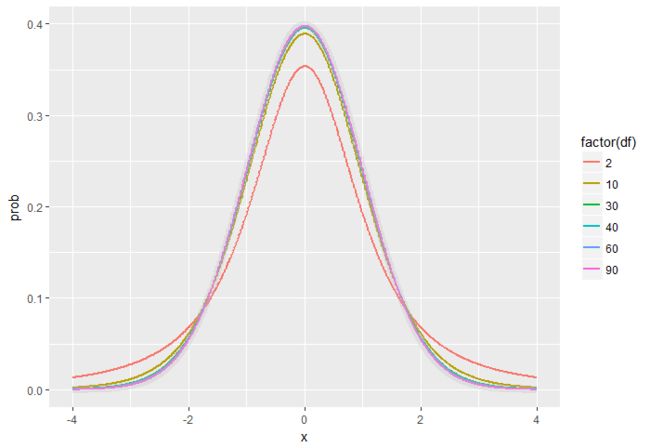
1. t分布(不同自由度)
了解r语言几个函数:dt,pt,qt,rt分别与dnorm,rnorm,pnorm,qnorm和rnorm对应
- dt() 的返回值是正态分布概率密度函数(density)
- pt()返回值是正态分布的分布函数(probability)
- 函数qt()的返回值是给定概率p后的下百分位数(quantitle)
- rt()的返回值是n个正态分布随机数构成的向量
x <- seq(-4, 4, length=200)
df <- c(2, 10, 30, 40, 60, 90)
require(plyr)
get.pt <- function(x, df) {
prob <- dt(x, df)
dd <- data.frame(x=x, df=df, prob=prob)
return(dd)
}
pt.df <- mdply(data.frame(x= rep(x, length(df)), df=rep(df, each=length(x))), get.pt)
require(ggplot2)
ggplot(pt.df, aes(x, prob))+geom_line(aes(group=df, color=factor(df)), lwd=1)+geom_line(data=data.frame(x=x, prob=dnorm(x)), alpha=0.3, lwd=3, color="gray")
2. 单样本t检验(使用教材光盘血红蛋白数据: 例03-05.sav)
前提条件:取自正态分布的小样本(<=60, 偏态用秩和检验);或者取自任意分布的大样本(>60)
# install.packages("memisc")
library(memisc)
hb_df <- data.frame(as.data.set(spss.system.file('E:\\医学统计学光盘文件\\SPSS文件_医学统计学(第4版)\\各章例题SPSS数据文件\\例03-05.sav')))
t.test(hb_df$hb, mu=140)
One Sample t-test
data: hb_df$hb
t = -2.1367, df = 35, p-value = 0.03969
alternative hypothesis: true mean is not equal to 140
95 percent confidence interval:
122.1238 139.5428
sample estimates:
mean of x
130.8333
除此之外,还可以直接计算出t值后,使用pt函数计算p值
t.value <- abs((mean(hb_df$hb) - 140) / sd(hb_df$hb) * sqrt(nrow(hb_df)))
p.value <- pt(t.value, df=nrow(hb_df)-1, lower.tail=FALSE)*2
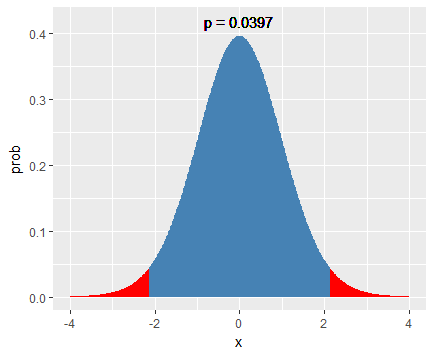
可视化:
x=seq(-4, 4, length=500)
d <- data.frame(x=x, prob=dt(x, df=length(hb_df$hb)-1))
require(ggplot2)
ggplot(d, aes(x, prob, fill=((x>-t.value & x3. 配对样本t检验(paired/matched t-test)教材光盘数据:例03-06.sav
前提条件:配对设计(同质对子接受两种不同处理;同一样品接受不同处理;同一对象接受处理前后)
- 方法 1:
# install.packages("memisc")
library(memisc)
paired_df <- data.frame(as.data.set(spss.system.file('E:\\医学统计学光盘文件\\SPSS文件_医学统计学(第4版)\\各章例题SPSS数据文件\\例03-06.sav')))
t.test(paired_df$x1, paired_df$x2, paired=TRUE)
- 方法 2:
d <- (paired_df$x1-paired_df$x2)
t.value <- abs(mean(d)/sd(d)*sqrt(length(d)))
p.value <- pt(t.value, df=length(d)-1, lower.tail=FALSE)*2
4. 两样本t检验(成组t检验Two Sample t-test)教材光盘数据:例03-07.sav
前提条件:小样本,需要方差齐性和来自正态总体(方差不齐需用近似t检验);或者大样本(>60)
- 方法 1:
# install.packages("memisc")
library(memisc)
group_df <- data.frame(as.data.set(spss.system.file('E:\\医学统计学光盘文件\\SPSS文件_医学统计学(第4版)\\各章例题SPSS数据文件\\例03-07.sav')))
t.test(group_df$x[group_df$group=="阿卡波糖胶囊"], group_df$x[group_df$group=="拜唐苹胶囊"], paired=FALSE)
- 方法 2:
library(plyr)
group_dd <- ddply(group_df, .(group), function(x) data.frame(SD=sd(x$x), n=length(x$x), mean=mean(x$x)))
diff_se <- sqrt(sum(group_dd$SD^2*(group_dd$n-1))/sum(group_dd$n-1)*sum(1/group_dd$n))
t.value <- abs((group_dd$mean[1]-group_dd$mean[2])/diff_se)
p.value <- pt(t.value, df=sum(group_dd$n)-2, lower.tail=FALSE)*2
5. 正态性检验
一般不必要使用,多用于采用正态分布法制定参考值范围时
正态性检验之qq plot与pp plot原理介绍
正态性检验之矩法(method of moment)计算偏度skewness和峰度kurtosis
6. 方差齐性的F检验,教材光盘数据:例03-06.sav
F检验理论上需要满足资料服从正态分布,进行方差齐性检验更多采用另一种不依赖总体分布形式的Lecene检验
进行f和t一样,r语言有df,pf,qf,rf和var.test等函数
- 方法 1:
# install.packages("memisc")
library(memisc)
group_df <- data.frame(as.data.set(spss.system.file('E:\\医学统计学光盘文件\\SPSS文件_医学统计学(第4版)\\各章例题SPSS数据文件\\例03-07.sav')))
var.test(group_df$x[group_df$group=="阿卡波糖胶囊"], group_df$x[group_df$group=="拜唐苹胶囊"])
- 方法 2:
f.val <- sd(group_df$x[group_df$group=="阿卡波糖胶囊"])^2/var(group_df$x[group_df$group == "拜唐苹胶囊"])
p.val <- pf(f.val, df1=19, df2=19, lower.tail=FALSE)*2
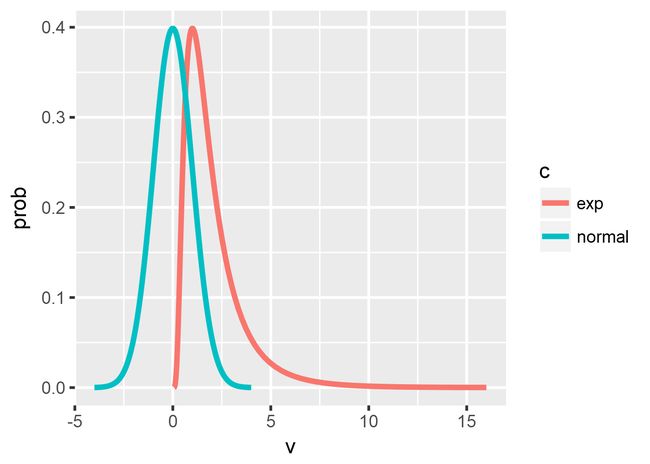
7. 变量变换
对数变换:数据效应为相乘,变异系数接近常数
b <- rnorm(100)
prob <- dnorm(b)
a <- exp(b)
data <- data.frame(variable=c(a, b), c= rep(c("exp", "normal"), each=length(a)), prob=c(prob, prob))
CairoPNG(1400, 1000, file="myplot.png", dpi=300)
ggplot(data, aes(v, prob, color=c))+geom_line(lwd=1)
dev.off()
cvs <- c()
for (i in 1:1000) {cvs <- c(cvs, (raster::cv(sample(a, 79))))}
hist(cvs, breaks=100)
- 平方根变换:适用于Poisson分布资料,方差与均数近似相等,轻度偏态(如发病的地域或时间分布)
- 反正弦变换:率或百分比的数据
- 倒数变换:两端波动大的数据
参考:
[1] 孙振球 徐勇勇. 医学统计学【第四版】
[2] https://guangchuangyu.github.io/statistics_notes/section-4.html#section-4.1