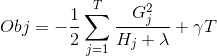目录
1、回顾:
1.1 有监督学习中的相关概念
1.2 回归树概念
1.3 树的优点
2、怎么训练模型:
2.1 案例引入
2.2 XGBoost目标函数求解
3、XGBoost中正则项的显式表达
4、如何生长一棵新的树?
5、xgboost相比原始GBDT的优化:
6、代码参数:
1、回顾:
我们先回顾下有监督学习中的一些核心概念:
1.1 有监督学习中的相关概念
我们模型关注的就是如何在给定xi的情况下获得ŷi。在线性模型里面,我们认为
![]()
i是x的横坐标,j是x的列坐标,本质上linear/logistic regression中的yi^都等于这个,只不过在logistic regression里面,分了两步,第一步ŷi=∑j wj xij,此时ŷi含义是一个得分,第二步你把这得分再扔到Sigmoid函数里面,才会得到概率。所以预测分值的ŷi在不同的任务中会有不同的解释。对于线性回归(linear regression)来说,ŷi就是最终预测的结果。对于逻辑回归(logistic regression)来讲,把ŷi丢到Sigmoid函数里面去,是预测的概率。在其它的一些模型里面,ŷi还有其它的作用。而在线性模型里面的参数就是一组w,叫做θ。即
![]()
对于参数型模型,要优化的目标函数有两项组成,一项是Loss,一项是Regularization。表达公式即
![]()
常见的损失函数Loss如:平方误差损失函数(square loss),表示为:
![]()
交叉熵损失函数(Logistic loss),表示为
![]()
正则项Ωθ是用来衡量模型简单程度的,有L1正则,即
![]()
有L2正则即L2范数的平方,乘一个λ。即
![]()
λ是我们要调节的超参数,用来衡量Obj函数到底是更在乎简单程度,还是更在乎在训练集上的经验损失。所谓经验损失就是你在训练集上错了多少就叫经验损失。对于不同的loss和不同的Regularization这两项加合起来,让这两项的和最小,就达到了一个兼顾的目的,所以它们俩都要相对比较小,才是最好的模型效果。如果说为了达到使L(θ)让它下降一点点,而Ωθ上升好多,就代表着过拟合。模型复杂度上升了好多才带来了一点点提升,这种事情并不是我们想要的。我们希望一个简单的模型,能给我一个最好的答案;如果做不到这俩的话,也希望一个相对简单的模型给我一个相对比较好的结果就行了。加法在这里面达到了兼顾的目的。
对于不同的loss和不同的Regularization组合,再对它进行最优化,就构成了我们所谓的不同的算法。
比如对于mse损失函数组合一个L2正则就是岭回归,表达为:
![]()
对于mse损失函数组合一个L1正则就是lasso回归,表达为:
![]()
对于Logistic loss交叉熵损失函数组合一个L2正则就叫做逻辑回归,表达为:
所以逻辑回归的损失函数里必定会带这λw^2这项,没有这项就不能叫做逻辑回归。
1.2 回归树概念
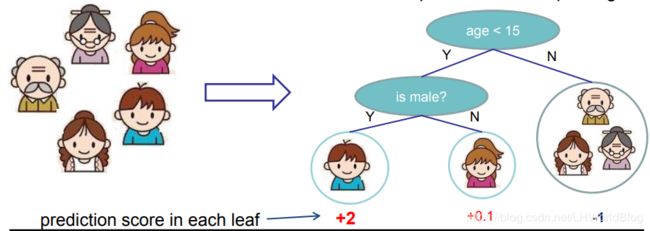
在来回顾下回归树的相关概念,对于回归树(CART树Classification and Regression Trees)来讲,它的决策的分裂条件和决策树是一样的,也是多次尝试分裂,哪次结果最好就留下来。最后它会得到一个叶子节点,也能表达是一个连续的值,我们在此称之为score分数,对于回归树我们得到的是一组分数。比如下面例子:
我们要判断这个人是否喜欢电脑游戏,通过一个回归树来训练,年龄小于15的点被分到左边,是否是男的分到左边。所以小男孩最终落到了左边叶子节点,小女孩通过分裂落在了右边叶子节点,而另外三位落到了右边叶子节点。最终通过某种方法,先不用考虑是什么方法,它通过y平均得到了小男孩得分是+2,小女孩+0.1,而另外三位对于计算机游戏的喜好程度是-1,这是一个回归树的形式。
1.3 树的优点
树有这么一个优势,就是inputs对于输入数量的大小,不太在意。做分类,原来最强的霸主是SVM,但它有一个问题就时间复杂度是O(n3)。所以它在小数据集上表现得非常好,代码也跑得起来,但一旦到海量数据集上,它就会变得不可接受。如果一千条数据用十分钟,10万条数据可能就以年来记了。三次方实在太可怕了,这是它最慢的情况,当然它内部也做了一些优化,不是所有情况都会达到O(n3)。但是树的训练基本就是O(n)或者O(n*m),它需要遍历所有的维度,它比O(n3)要scaling了好多,scaling在机器学习领域特指的是小数据量上表现的好不好,在小数据量上能跑的,在大数据量上还跑得起来的这个方面的性能。 这是一个非常重要的特性。树模型最不怕的就是这个东西,它表现的时间复杂度比较稳定。另外它对于数据集的是否归一化,不需要太过在意,参数型模型里y是通过x计算出来的,它们之间有一个等式关系,而对于树一系列的模型来讲,x和y实际上是被割裂开的。x值只用来分裂,跟y值最后的结果没有直接的计算关系,它有间接的关系。y的计算结果是通过落在叶子节点上的其它的y算出来的,而不是通过x算出来。
这里先给大家铺垫下,在xgboost中,第一,它虽然用的是CART树,但它叶子节点的表达,不再像以前使用y平均了,但是它仍然是一颗回归树,不再是计算纯度的分类树。第二,它判断分裂条件的标准也不再是方差了,而是看损失函数下降的高低。所以它虽然形式上是一颗回归树,但无论分裂条件的判断,还有叶子节点的表达,跟我们之前讲的回归树不一样了。
2、怎么训练模型:
实际上永远咱们讲模型是这个套路,先模型假使已经从天上掉下来了,你要怎么用它也就是预测部分,理解了怎么预测之后,咱们再讲它是怎么得到这模型的,怎么训练出来的。
2.1 案例引入
那么我们该如何学到一堆树?首先要定义一个损失函数或者目标函数,包括损失项和正则项,然后去优化它。
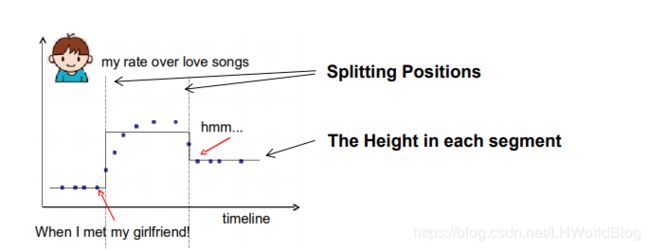
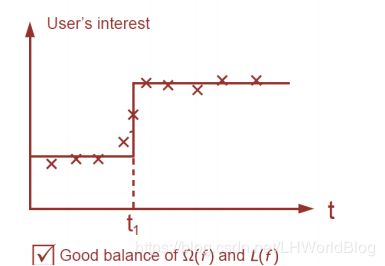
先看个例子:我想要预测到底在t时刻有多么的喜欢浪漫的音乐,以下图两个时间节点来学到了这么一棵树(实际上我们知道做回归树就是在上面画锯齿),当所有小于左边图中时间节点的时候,用这几个点的平均值代表叶子节点的预测;当大于右边节点的时候,用这些点的平均值代表叶子节点的预测。中间也是一样。假设左边这个点是我遇到女朋友的时候,接下来你会越来越喜欢romantic music一直到后边,对于浪漫音乐喜好程度又开始下降了。
对于这个模型来说分了两支,因为决策树就怕过拟合,它如果没做预剪枝的话,会一直细分下去。
这是一个实际的例子,通过这个例子,我们可以得到对于普通的一棵树来说,我们要学习的是:第一,splitting positions,意思是分裂的位置,也就是分裂条件应该设在哪,第二我们要学得每一段的高度,也就是指这个区间内叶子节点表达应该等于多少,因为它是取叶子结点的平均值作为结果。
基于这两个因素,我们怎么定义这个树是复杂还是不复杂呢?首先有多少个分裂点可以看出它复杂还是不复杂,如果它切的更碎,正则项也就更多更复杂;另外一个类似L2正则的方式,就是每一段的高度的L2正则,也可以像逻辑回归,线性回归一样,一定程度上衡量叶子节点有多么的复杂。所以它提出了两种思想,第一个是分裂的次数可以衡量这个树复杂不复杂,第二分裂之后每个树给你一个score结果,这个结果做一个平方再加和的总体值,也可以一定程度上衡量这个树到底复杂不复杂。
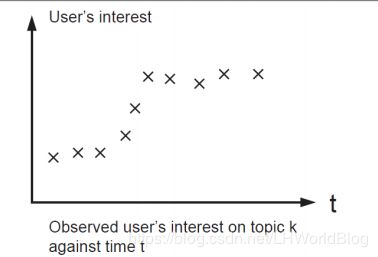
比如对于如下的树我们用以上的定义复杂的因素来评判下:
分裂几种情况,第一种情况:
对于这么一个要分类的结果,显然它会造成Loss小,因为它非常好的拟合了训练集;如果简用分裂次数和段高低的平方加和来讲,正则项会很大。
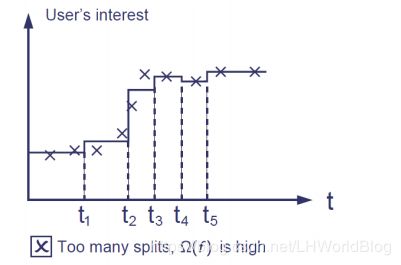
第二种情况:
它在不对的splitting point上分割了,导致L大了,而Ω项还可以,因为它只做了一次分裂。
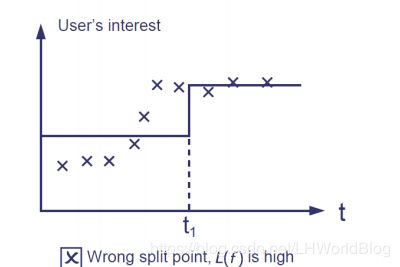
第三种情况:
就是一个非常好的平衡,只做了一次分裂,并且损失项还比较小,所以我们的目标就是在训练树上也应该去衡量一下树的复杂程度,能让它做到即训练损失小一些,并且正则项也要小一些。
2.2 XGBoost目标函数求解
对于集成学习,我们知道是把多棵树的结果给累加起来。假设我们有K棵树,最终的ŷ就是K棵树的预测结果的相加。表达为:
这里面的F是我们所有的回归树,就之前的线性模型来讲,它的参数是一组w,而在这个里面,它的参数是就一堆树。所以原来参数型模型我们要学的目标是一组权重w,是我们要的结果,而树的集成学习模型,我们要学到的是一堆树,这是要从训练集中学到的。基于此,我们建立一个目标函数的形式即:
其中第一项是损失函数,损失函数既然每颗小树里面没有w,我们也就不费事地把它翻译成w的语言了,直接把ŷ拿来用,一定是有了yi,y^这两项就能算损失函数的,这是损失部分,跟GBDT里面的损失是一个概念。而另一项Ω是新引入的。这个公式里面从1到K,从一到n分别代表什么含义? n是样本的数量,K是树的数量。你有n条样本,统计损失的时候,n条样本都要考虑进去,而有K棵树在统计复杂度的时候,要以树为单位去统计。
如何去定义Ω这个东西?它提出了几种思路:
第一每棵树叶子节点数量,可以描述这个树的复杂程度。
第二每棵树叶子节点上的评分score的L2范数也可以评估这棵树是否复杂。
第三把这上面两项结合在一起,做了一个正则项。
现在既想要一个有一定的预测效果,而相对简单的模型,要怎么做呢?我们给集成学习将Ft(x)写成如下的形式:
这里的yi^代表之前写的大F(x),y^0就是F0(x),y^1就是F1(x),一直到Ft(x)。通过boosting这种加法模式,最终的ŷ就等于之前所有小树的加和,也等于上一代的ŷ加上最新的一棵小树。此时Loss中的ŷ是什么的问题就解决了。
我们把它分解一下,既然
![]()
此时Obj函数就变成了
我们现在的目标就是找到一个f(t),能够使这个函数变小。只要这个函数小了,预测结果一定差不了。这个函数带着求和号就代表着它已经考虑到所有样本的情况了。
如果我们的损失函数是mse的话,将上式中的l替换成具体的损失函数就是:
yi^2和yi^(t-1)^2这两项都可以放到后面的常数项里面去,它们不会影响ft(xi)这一项的变大或者变小,只有它的系数可以影响。所以整合完后就是如上所述的公式,其中ft(xi)是未知数。所以这就变成了一个简单的二次函数求最小值的问题。
ax^2+bx+c当x等于什么的时候有最小值?根据初中的理论,当x为-b/a2的时候,函数有最小值。此时在上述公式里面
a是1,b是
所以当ft(x)为yi-yi^(t-1)的时候,函数取最小值。这就是我们说的残差,所以残差你从这个角度也可以一样推出来,我们希望损失函数可以最小,就是当ft(x)为yi-yi^(t-1)的时候最小,这里面为什么我们要写成ft(xi)的形式,因为我们目标是要找到ft,所以一定要把它暴露出来,这样我们才知道ft要满足什么条件才可以。
mse函数是一个非常幸运的函数,它展开之后就是一个二次函数,你可以求出它最小值的解析解,对于逻辑回归函数甚至更复杂的函数你是没法写出解析解的,你就需要把目标函数展开成一个能写出解析解的东西来,再去求它的解析解,此时就用到我们的二阶泰勒展开。二阶泰勒展开的公式如下:
我们再看下我们的目标函数:
结合二阶泰勒展开的公式,这里把![]() 看作△x,把
看作△x,把![]() 看作x。进行二阶泰勒展开,x已知。对f(x)求一阶导是:
看作x。进行二阶泰勒展开,x已知。对f(x)求一阶导是:
![]()
上面的含义是对l求一次导,然后把y^(t-1)带进去。
对f(x)求二阶导是:
![]()
所以最后的二阶泰勒展开就是
在这个函数里面只有![]() 是自变量,同样这也是一个二阶函数,所以当x=-b/2a的时候,损失函数取得最小值,也就是ft(xi)=f''(x)/f'(x)的时候。如果看到这不理解的话,我们考虑下一个特殊的函数--平方损失函数。对于平方损失函数来讲,一阶导是二倍的残差,二阶导是一个常数2,即:
是自变量,同样这也是一个二阶函数,所以当x=-b/2a的时候,损失函数取得最小值,也就是ft(xi)=f''(x)/f'(x)的时候。如果看到这不理解的话,我们考虑下一个特殊的函数--平方损失函数。对于平方损失函数来讲,一阶导是二倍的残差,二阶导是一个常数2,即:
![]()
把它带进去二阶泰勒展开的式子里,会得到跟之前直接把它展开同样的结果。因为它本身是个二次函数,对于二次函数进行二阶泰勒展开没有损失,实际上是用一个抛物线去拟合一个抛物线,所以不会有约等于号。但是对于复杂一点的函数,比如说交叉熵损失函数,它就有损失了,但是有损失它也不在乎了,我就保留它的这些近似项。
再来对这个公式进行简化,
而![]() 这一项可以扔掉,因为它是常数项,yi是真实值,而y^(t-1),是前面t-1轮预测已经得到的结果,所以这里面的关于它两个的损失函数可以计算出来。现在只有
这一项可以扔掉,因为它是常数项,yi是真实值,而y^(t-1),是前面t-1轮预测已经得到的结果,所以这里面的关于它两个的损失函数可以计算出来。现在只有![]() 未知,剩余的都是可以算出来的。 我们把常数项放在一起,整理之后,新目标函数:
未知,剩余的都是可以算出来的。 我们把常数项放在一起,整理之后,新目标函数:
其中:
![]()
这里面简化之后虽然l丢掉了,但l实际上存活在gi和hi里,因为在计算gi和hi的时候,需要对l进行ft-1的求偏导,再把ft-1带进去,gi就是函数空间中梯度下降对应着如下结果:
gi和hi是什么东西?它已经是个能求得出来的真真切切的一个数。y^(t-1)是知道的,它是某一个数据点在上一轮预测出来的具体的结果值,对它求偏导的解析式也能知道,只要损失函数定义出来就知道了。求完偏导得到了一个新的函数,把具体的值代进去就得到了一个新的值。有多少条样本就有多少个gi和hi。
3、XGBoost中正则项的显式表达
我们目前把loss项已经整理好了,而Ω这一项还没显式地表示出来。我们最终想找到一个ft去让整个目标函数最小,gi和hi已经是具体的数了,而Ω这一项还没有定义。接下来我们来讨论下Ω的表达。
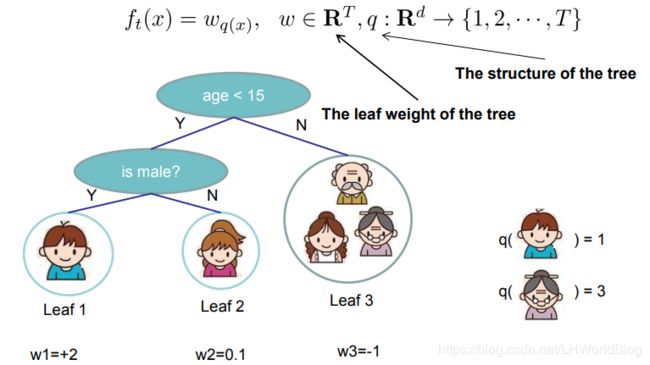
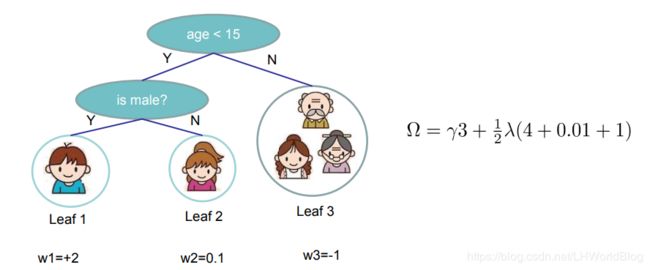
引入分配机的概念,它定义了ft(x)最终的预测结果就等于wq(x)。其中q(x)代表它落到了哪一个叶子节点上。假如说x第一条数据落到了第一个叶子节点上,这会的第一条数据就等于1。对于小男孩来说,它落到了一号节点上,q(小男孩)=1,也就是ft(小男孩)=wq(x)=w1,某一条数据最终会落在几号叶子节点上,q这条数据就等于几。也就是它定义了什么叫w,在这里面w1就是第一个叶子节点的表达,w2就是第二个叶子节点的表达,w3就是第三个叶子节点表达。
有了w的定义,我们定义Ω项,定义了损失项。损失项包含两部分,Ω是跟着每棵树来的,应该一棵树有一个Ω。也就是对于任何一个小树我扔到Ω里面,你就要给我评估出我树有多复杂。先看定义公式:
对于某一棵树的正则项来讲,它就等于叶子节点的数量乘以第一个超参数γ,这个是设置的。然后就是这棵树上的每一个叶子节点的表达的平方加和,再乘1/2λ。比如下面这个树它的Ω等于多少?
它有三个叶子节点,就是3乘以γ,w1等于+2,平方是4,w2平方等于0.01,w3平方等于1。所以最终的正则项是上述表达,也就是说对于这棵树的Ω,在确定了这两个超参数之后,也是一个可以具体计算的数。
我们再看下一种表达,假设![]() ,它是一个样本的集合,所有被分到一号叶子节点里边的样本的集合就叫I1,所有分到二号叶子节点里边的集合就叫I2。 然后ft(x)写成wq(x),最后我们的损失函数就表示成:
,它是一个样本的集合,所有被分到一号叶子节点里边的样本的集合就叫I1,所有分到二号叶子节点里边的集合就叫I2。 然后ft(x)写成wq(x),最后我们的损失函数就表示成:
解释下:
从第一步到第二步应该没有问题就是把正则的具体表达带入进去,而第二步到第三步实际上就是我们换一种遍历的维度,原来是样本序号,从样本i=1遍历到n,现在改成遍历叶子节点j=1到T,从1号叶子节点里数,所有属于1号叶子节点的gi做一个加和,统一乘wj。比如有三个叶子节点,其中1,2号样本落在第一个,所以表达为w1。3,5落在第二个叶子结点,表达为w2。4,6落在第三个叶子结点,表达为w3。根据第二个公式的加法![]() 就是g1w1+g2w1+g3w2+g4w3+g5w2+g6w3,而现在根据第三个公式表达的就是(g1+g2)w1+(g3+g5)w2+(g4+g6)w3,实际上这一项的转换就是把相同的w给提到一起去,也就相是同叶子节点里边的g都加和到一起。
就是g1w1+g2w1+g3w2+g4w3+g5w2+g6w3,而现在根据第三个公式表达的就是(g1+g2)w1+(g3+g5)w2+(g4+g6)w3,实际上这一项的转换就是把相同的w给提到一起去,也就相是同叶子节点里边的g都加和到一起。
另一项
按叶子节点遍历,就是
而结合最外面的正则项,刚好也是按叶子节点遍历,所以干脆合到一起,就变称第三个公式的表达。
原来是按样本遍历,但这样本里面肯定有很多点落在同一个叶子节点里了,也就是这些点,未来的wq(xi)都是相同的。我们就把它以叶子节点来遍历,把所有属于一号叶子节点的gi,虽然它们落在同一个叶子节点里了,但是它们的gi不一定相等,取决于这条样本在上一轮预测中它落在哪一个叶子节点。
通过显示的定义的Ω,我们就把目标函数整理成了如下形式:
这就是我们的目标函数。 现在这个目标函数只看wj的变化而变化了。我们定义Gj等于落在某一个叶子节点上的所有gi的加和, Hj定义为落在某一个j叶子节点上所有hi的加和。即:
最后损失函数表示为:
现在这个损失函数是大还是小,取决于谁呢?GjWj是已经知道的,Hj这一项也是知道的,λ是自己设的超参数,只有wj是未知的。当它等于什么的时候能让Obj最小呢?这又是一个二次函数,当x=-b/a2的时候最小,在这里wj是未知数,b是Gj,a是1/2(Hj+λ),所以根据表达式,即wj如下的时候:
能让损失函数等于最小值。此时损失函数根据一般的二次方程的最小值表达形式-b^2/4+c,此时损失函数的最小值可以表达出来如下:
这是一个简单的二次函数,函数的最小值解能写出来。
所以我们可以看到叶子节点的表达不再等于y平均了,而等于上面wj的表达。
举个例子,假设有这么一棵树:
分到一号叶子节点有的第一号样本,分到二号叶子节点有第四号样本,分到第三个叶子节点有235,三个样本。此时的G1就是小男孩的g1,H1就是小男孩的h1。G3=g2+g3+g5,H2=h2+h3+h5。最终的得分,左边为什么是+2?g1就应该等于前面所有的树对y的偏导,算出了具体的值。对它再求一次偏导,算出h。g1,h1是具体数,每一条样本都可以带到一阶导和二阶导的函数里面,算出它的g和h。在分裂的过程中,如果分到了同一个叶子节点,要把它们所有的g,h相加,再带到刚才obj公式里面去,算得一个叶子节点表达即2。所以叶子结点的表达就不再是平均了,而变成了跟以前的预测结果相关的。
4、如何生长一棵新的树?
假如我想训练第T+1棵树,也是就f(t+1),那你在手里有什么,你其实有个FT,你手里还有一个训练集,根据这些我们能得到从g1一直到gn,从h1一直到hn。它们每一个都是训练集背后具体的一个数。
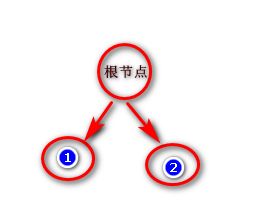
我们看下从最开始的首先一个根节点,这个根节点里包含了n条数据。你每次分裂,就像树一样,变例所有可能的分裂的维度,每次分裂,都能算一下此时的obj等于多少,Obj是关于G和H的,然后再求和,在加上一个t倍的γ,你每尝试一次就算一次obj,是不是总能找到一个使得obj最小的那个标准,固化在这,没问题吧?
上面是两个叶子结点。
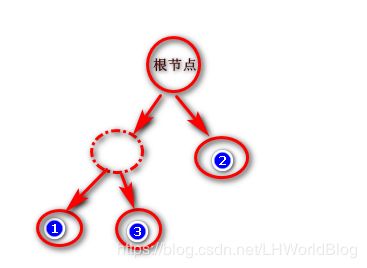
接下来我该试着下一次分裂是不是左边的节点又能一份为二,如下:
分完之后这棵树变为3个叶子结点,然后1里边落哪些,你每次分裂的时候。假如这棵树就是现在这个额结构,那么我obj应该能等于多少也可以求出来。所以肯定能够找到使得obj最小的的分裂去分他,没问题吧。然后再一次的对1号节点分裂,然后发现,无论选择哪一个分裂,obj都没有下降,此时怎么办,不分裂了,它就是叶子结点了,那你知道这是叶子结点了要去计算这个叶子结点未来怎么表达啊,怎么表达呢,用刚才那个![]() 来表达,这个节点固定死在这了,这个节点里有哪些样本,也都知道了,G知道了,H也知道了,λ是你自己写的,这个节点就这样了。接下来再去找2号节点分裂看下能不能使得损失函数再下降一下,能下降就分,不能下降就不分了,接着去算这个叶子节点的表达,这个实际上就是树分裂学习的方法。
来表达,这个节点固定死在这了,这个节点里有哪些样本,也都知道了,G知道了,H也知道了,λ是你自己写的,这个节点就这样了。接下来再去找2号节点分裂看下能不能使得损失函数再下降一下,能下降就分,不能下降就不分了,接着去算这个叶子节点的表达,这个实际上就是树分裂学习的方法。
当然也会有预剪枝的条件,xgboost里边也有最大深度来让你设置,那么它到底是听最大深度的呢,还是听损失函数的呢,哪个先达到底线,就听那个,假如说损失函数还没达到最大深度已经不下降了,那他它也不会在训练了,假如损失函数还想着自己还有潜力再下降,但是已经达到最大深度,此时也不在下降了。
以上就是如何长成新树的流程。总结下,初始所有样本都在同一个根节点里,当它一分为二了,选定所有分裂条件都试一试,注定有一部分节点落在左边,一部分节点落在右边。只要这次分裂分出来了,G和H就可以算了,T也就知道了。此时就可以看Obj的函数等于多少?原始的损失函数能算,分出来之后的损失函数函数,看哪次下降的最多,就把那次分裂作为这一次的分裂条件保存下来,随着每次分裂,T一定会+1,每分裂一次叶子节点就会多一个。
Loss这一项会下降,下降了的这个值一定要胜过+1这个值,它才会认为目标函数下降了,否则就是没带来多大提升,还白白的多弄出来一个叶子,这样效果不好。
所以xgboost不需要人工剪枝,它通过正则项就把剪枝的能力赋予它了,当它生长发现注定会+1的情况下,而遍历了所有维度,发现没有一个能打败这个东西+1的损失的,它就停止生长了。 相当于自动的剪枝。
如何去搜索条件分裂?就是一个线性搜索挨个尝试在不同位置进行分裂。哪种分裂能带来最大的增益,就保留哪一个条件作为分裂条件。实际上它定义了增益的形式,增益就等于
这是分裂后的目标函数的值减去旧目标函数的值,也就是左子节点的得分![]() ,加上右子节点的得分
,加上右子节点的得分![]() 。减去不分裂的得分
。减去不分裂的得分![]() 。因为每一次新的分裂叶子结点永远只增加一个(可参考上面图例),而每一次分裂的得分都带一部分λT,所以λ(T+1)-λT=λ。也就是上式为什么带个λ的原因。
。因为每一次新的分裂叶子结点永远只增加一个(可参考上面图例),而每一次分裂的得分都带一部分λT,所以λ(T+1)-λT=λ。也就是上式为什么带个λ的原因。
5、xgboost相比原始GBDT的优化:
1、原始GBDT是一个原始空间的梯度下降,它实际上是对损失函数进行一个一阶的展开,去求这个一阶泰勒展开的近似,而xgboost采用二阶泰勒展开拟合目标函数的L部分。也就是类似牛顿法来使函数收敛的次数更快,所以它需要更少棵树,就可以达到一个比较不错的预测结果,这是它的理论依据。
2、xgboost还增加了一个正则项,
来防止过拟合。
3、它引入了缩水系数,大F(x)是若干f(x)的加和,我们每次新训练一棵树,也要给它加一个学习率进去,也就是f(x)前面也加了一个学习率,叫η。即ηf(x)。所以新的大F(x)表达即为![]() 。如果η为1,就没有缩水,每次加的就是得到损失函数最小的那个小树。
。如果η为1,就没有缩水,每次加的就是得到损失函数最小的那个小树。
4、xgboost 有自己的剪枝策略。对于剪枝它不需要特意的去确定,只要把超参数确定了,γ和λ确定了之后,它会自动的根据损失函数到底是上升了还是下降了,决定是否还要继续分裂下去。
5、它天生可以应对缺失值,在它的实现里边对缺失值做了一些处理。
6、它可以自定义损失函数传进去,损失函数需要传一个g和h的返回,你定义两个方式就可以。
7、它支持集群运算。通常我们说Boosting是不支持集群运算的,根据这棵树的预测结果,甚至所有树的结果来生成下一个树。工作量在训练树中的排序部分,我们说每次分裂都要去对可能的条件做一个线性搜索,然后排序,在排序的过程中,它会可以通过集群,多任务来跑排序。虽然我们以树为粒度,我们没有办法把它分配到多个机器上跑,但是以树内部的分类归并排序,在集群上来跑,所以这样它一定程度上支持了集群。
6、代码参数:
它有哪些超参数?
max_depth:虽然它不需要设置预剪枝,但同样可以强制的设一下树的深度,强制不要让它走太深。
learning_rate:就是刚才说的缩水系数,学习率。
n-estimators:总共树的棵数,对应着牛顿法里面的迭代次数。
silent:true和false取决于它会不会在你的控制台打印它训练的一些损失,你能看到损失在第多少棵树的时候就不再变化了,达到低谷收敛了。
objective:目标函数,它默认提供了mse , Logistic,也就是用逻辑回归做的二分类、multiclass,还有一些其它的。另外一个非常厉害的地方,是它支持你自己定义损失函数,在objective可以传入一个函数进来,它要求g和h分别怎么算,告诉它求完一阶导之后等于什么,二阶导之后等于什么就行了。它要g和h是怎么算,输入一个yi一组序列,输入一个ŷi,然后算出所有g和h。
subsample:每次训练小树的时候,要从训练集中行抽样了多少,如果设置这个参数,便不再是有放回的随机抽样了,默认是1。随机森林它一定是有100万条数据,它生成的每一个子数据集都是100万条数据,因为它没有subsample,你不可以设置,它就是1。
Colsample-bytree:代表每次训练一棵树的时候,要不要少给它一些维度让它看, 1是100%的意思。

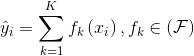
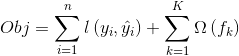
![\sum_{i=1}^{n}\left[g_{i} f_{t}\left(x_{i}\right)+\frac{1}{2} h_{i} f_{t}^{2}\left(x_{i}\right)\right]+\Omega\left(f_{t}\right)](http://img.e-com-net.com/image/info8/8fe9bda86d8e492e8b5cb57da2af775c.gif)
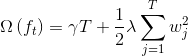
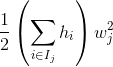
![O b j^{(t)}=\sum_{j=1}^{T}\left[\left(\sum_{i \in I_{j}} g_{i}\right) w_{j}+\frac{1}{2}\left(\sum_{i \in I_{j}} h_{i}+\lambda\right) w_{j}^{2}\right]+\gamma T](http://img.e-com-net.com/image/info8/2fd57de56bd84264b785dbdc73c79460.gif)