参考:
1- fft相位谱
实验
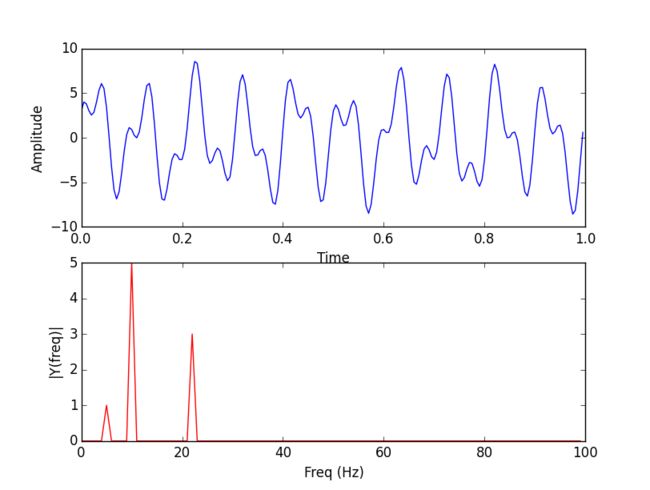
信号的表达式:f = sin(2*pi*5*t)+5*sin(2*pi*10*t)+3*cos(2*pi*22*t)
目的:学会使用fft函数分析信号
实验过程
- 设置采样频率、计算信号长度
设置采样频率为200点,采样区间为[0,1]直接使用采样周期作为步长分割区间,因此得到的信号长度于采样频率相等为200点
由于信号的最大周期为0.2s,
[0,1]区间包含了5个周期,共采200点,即每个周期内采样40点,频率倍数为8倍,能满足奈奎斯特采样定律大于2.56倍的要求
- 计算幅频图的参数
纵坐标为幅值
fft变换后的y数组中的值其实就是傅立叶系数ak,因此幅值就是|ak|,ak为复数(实数是虚部为0的复数),对复数求模就是复数的实部平方+虚部平方,再开更号,实数的取绝对值运算就是其特例。因此使用abs()函数就能求得幅值~。取值在左右两端对称,因此只要取一半的数据绘图即可
横坐标为频率
频率与采集的信号长度有关,由于傅立叶变换在具有对称性,因此只要取一半的信号长度作为横坐标即可
- 得到信号长度,将其转化为数组k
- 取数组的一半作为横坐标
有了横纵坐标就可以愉快的画图了_
更新: 上述为幅频图,每个成分的频率知道了,还需要知道相位,即t=0时刻的值,相位可以通过公式arctan(-real/imag) 得出
2017-1-5更新: fft_bug?
fft的问题,中间部分不为零?
array([ 2.3, 3.4, 2.2, 0. , 0. , 0. , 0. , 0. , 0. , 0. ])
ipdb> np.fft.fft(zw)
array([ 7.90000000+0.j , 5.73049517-4.09079419j,
1.57082039-4.52671971j, -0.53049517-1.9404646j ,
0.22917961+0.09385448j, 1.10000000+0.j ,
0.22917961-0.09385448j, -0.53049517+1.9404646j ,
1.57082039+4.52671971j, 5.73049517+4.09079419j])
ipdb> np.fft.fft(zw[3:-1])
array([ 0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j])
ipdb> np.fft.fft(zw)
array([ 7.90000000+0.j , 5.73049517-4.09079419j,
1.57082039-4.52671971j, -0.53049517-1.9404646j ,
0.22917961+0.09385448j, 1.10000000+0.j ,
0.22917961-0.09385448j, -0.53049517+1.9404646j ,
1.57082039+4.52671971j, 5.73049517+4.09079419j])
实验结果(幅频图+相频图)
# numpy知识点
# numpy中取得复数的实部和虚部
# 快速过滤: arr[abs(arr)<0.0001]=0-1j
import matplotlib.pyplot as plt
import numpy as np
Fs = 200.0 # sampling rate
Ts = 1.0/Fs # sampling interval
ff = 5 # frequency of the signal
# t = np.linspace(0,1,Fs) # time vectori #使用linspace时幅频图出现小的波动
t = np.arange(0,1, Ts)
#frequency ff=5
# y = np.sin(2*np.pi*ff*t)+5*np.sin(2*np.pi*2*ff*t)+3*np.cos(2*np.pi*22*t)
# 加入相位
y = np.sin(2*np.pi*ff*t+ np.pi/6)+5*np.sin(2*np.pi*2*ff*t)+3*np.cos(2*np.pi*22*t)
#set frequency
n = len(y) # length of the signal
k = np.arange(n)
frq = k[range(n//2)] # one side frequency range
# Y = np.fft.fft(y) # 不做normaliztion幅值将放大为采样点数的1/2倍
Y = np.fft.fft(y)/(n/2.0) # fft computing and normalization
Y = Y[range(n//2)]
amplitude=abs(Y) # 获得幅值
threshold = 0.005 # 过滤极小值点的阈值
# 得到有用数据的索引
'''
x_vline=[]
for i, data in enumerate(amplitude):
if data>0.0001:
x_vline.append(i)
'''
# 使用列表推导式代替上面几行
x_vline=[i for (i, data) in enumerate(amplitude) if data > threshold]
y_amp=amplitude[x_vline]
# Y.real 得到实部,一个array; Y.imag 得到虚部,一个array
y_pha=np.arctan(-Y[x_vline].real/Y[x_vline].imag) # 获得相位
# 过滤相位中的极小值点
y_pha[abs(y_pha)实验结果(幅频图)
从图中可以得到基波
sin(2*pi*5*t) 与 另外两谐波的
频率和
幅值,与信号函数的组成一致
注意点
- 经过傅立叶变换后的值为复数,需要取绝对值,将它投影到实数轴上才能表示信号的幅值,直接使用复数做图,python会丢弃虚部,只将实数部分进行绘图
- 采样区间的长度影响频率的表示,将采样区间的长度设置为1,变换后的频率表示为信号频率,如果长度为2,3...则频率会扩大相应的倍数
- 采样频率影响傅立叶变化的能够表示的频率上限值
源程序(python)
import matplotlib.pyplot as plt
import numpy as np
Fs = 200.0 # sampling rate
Ts = 1.0/Fs # sampling interval
ff = 5 # frequency of the signal
t = np.arange(0,1,Ts) # time vector
#frequency ff=5
y = np.sin(2*np.pi*ff*t)+5*np.sin(2*np.pi*2*ff*t)+3*np.cos(2*np.pi*22*t)
#set frequency
n = len(y) # length of the signal
k = np.arange(n)
frq = k[range(n//2)] # one side frequency range
Y = np.fft.fft(y)/(n/2.0) # fft computing and normalization
# 为什么要做normalization?
Y = Y[range(n//2)]
fig, ax = plt.subplots(2, 1)
ax[0].plot(t,y)
ax[0].set_xlabel('Time')
ax[0].set_ylabel('Amplitude')
ax[1].plot(frq,abs(Y), 'r') # plotting the spectrum
ax[1].set_xlabel('Freq (Hz)')
ax[1].set_ylabel('|Y(freq)|')
plt.show()