自定义View-第十一步：Matrix

前言

根据Gcssloop所学习的自定义View整理与笔记。
这一节理论比较多，一定要耐心~

知识唤醒

矩阵乘法

一.Matrix初识

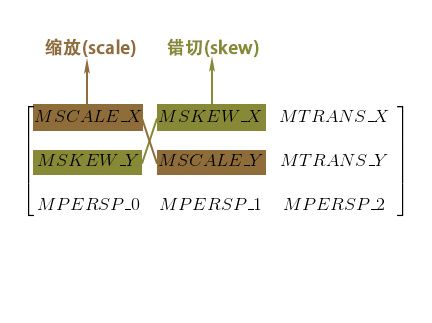
1. 基本变换

平移旋转

缩放错切

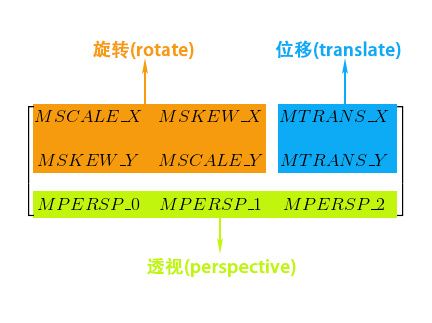
** 最后三个参数是控制透视的，这三个参数主要在3D效果中运用，通常为(0, 0, 1)**
上面的矩阵便是Matrix的数据结构，Matrix其实就是一个矩阵。

1. 前乘pre、后乘post、设置set

前乘pre相当于矩阵的右乘：M'=M*S；
后乘post相当于矩阵的左乘：M'=S*M；
设置set直接覆盖掉原来的数值。
这里，针对前乘和后乘详细的说一下，莫晕⤵️
前乘后乘是要一步步的执行的，而我们之前说过pre越靠后的先执行，是一种快速推测结果的方式，并不是计算的顺序，计算顺序可以参考Matrix详解。

二. Matrix方法

方法类别	相关API	摘要
基本方法	equals hashcode toString toShortString
数值操作	set reset setValues getValues	设置重置设置数值获取数值
数值计算	mapPoints mapRadius mapRect mapVectors	计算变换后的数值
设置set	setConcat setRotate setScale setSkew setTranslate	设置变换
前乘pre	preConcat preRotate preScale preSkew preTranslate	前乘变换
后乘post	postConcat postRotate postScale postSkew postTranslate	后乘变换
特殊方法	setPolyToPoly setRectToRect rectStaysRect setSinCos	特殊操作
矩阵相关	invert isAffine isIdentity	求逆矩阵是否为仿射矩阵是否为单位矩阵

1. 构造方法

无参构造

 Matrix matrix = new Matrix();

创造出来的是单位矩阵，如下：

有参构造

Matrix matrix = new Matrix(src);

创建一个Matrix，并对src深拷贝(理解为新的matrix和src是两个对象，但内部数值相同即可)

2. 基本方法

equals：比较两个Matrix的数值是否相同
hashCode：获取Matrix的哈希值
toString：将Matrix转换为字符串：Matrix{[1.0, 0.0, 0.0][0.0, 1.0, 0.0][0.0, 0.0, 1.0]}
toShortString:将Matrix转换为短字符串[1.0, 0.0, 0.0][0.0, 1.0, 0.0][0.0, 0.0, 1.0]

3. 数值操作，控制Matrix里面的数值

void set (Matrix src)：没有返回值，有一个参数，作用是将参数src中的数值复制到当前Matrix中，如果参数为空，则重置当前Matrix，相当于reset。
void reset ()：重置当前Matrix，即将当前Matrix重置为单位矩阵。
void setValues (float[] values)：参数是浮点型的一维数组，长度需要大于9，拷贝数组中的前9位数值赋值给当前Matrix。
void getValues (float[] values)：getValues和setValues是一对方法，参数也是浮点型的一维数组，长度需要大于9，将Matrix中的数值拷贝进参数的前9位中

4. 数值计算

mapPoints
计算一组点基于当前Matrix变换后的位置，(由于是计算点，所以参数中的float数组长度一般都是偶数的,若为奇数，则最后一个数值不参与计算)。

(1) void mapPoints (float[] pts)： pts数组作为参数传递原始数值，计算结果仍存放在pts中。

// 初始数据为三个点 (0, 0) (80, 100) (400, 300) 
float[] pts = new float[]{0, 0, 80, 100, 400, 300};

// 构造一个matrix，x坐标缩放0.5
Matrix matrix = new Matrix();
matrix.setScale(0.5f, 1f);

// 输出pts计算之前数据
Log.i(TAG, "before: "+ Arrays.toString(pts));

// 调用map方法计算
matrix.mapPoints(pts);

// 输出pts计算之后数据
Log.i(TAG, "after : "+ Arrays.toString(pts));

//结果：
//before: [0.0, 0.0, 80.0, 100.0, 400.0, 300.0]
//after : [0.0, 0.0, 40.0, 100.0, 200.0, 300.0]

(2) void mapPoints (float[] dst, float[] src):src作为参数传递原始数值，计算结果存放在dst中，src不变,如果原始数据需要保留则一般使用这种方法。

// 初始数据为三个点 (0, 0) (80, 100) (400, 300)
float[] src = new float[]{0, 0, 80, 100, 400, 300};
float[] dst = new float[6];

// 构造一个matrix，x坐标缩放0.5
Matrix matrix = new Matrix();
matrix.setScale(0.5f, 1f);

// 输出计算之前数据
Log.i(TAG, "before: src="+ Arrays.toString(src));
Log.i(TAG, "before: dst="+ Arrays.toString(dst));

// 调用map方法计算
matrix.mapPoints(dst,src);

// 输出计算之后数据
Log.i(TAG, "after : src="+ Arrays.toString(src));
Log.i(TAG, "after : dst="+ Arrays.toString(dst));

//结果
//before: src=[0.0, 0.0, 80.0, 100.0, 400.0, 300.0]
//before: dst=[0.0, 0.0, 0.0, 0.0, 0.0, 0.0]
//after : src=[0.0, 0.0, 80.0, 100.0, 400.0, 300.0]
//after : dst=[0.0, 0.0, 40.0, 100.0, 200.0, 300.0]

(3) void mapPoints (float[] dst, int dstIndex,float[] src, int srcIndex, int pointCount) 可以指定只计算一部分数值。

dst:目标数据；
dstIndex：目标数据存储位置起始下标；
src:源数据；
srcIndex：源数据存储位置起始下标；
pointCount：计算的点个数


/**
  *  将第二、三个点计算后存储进dst最开始位置。
**/
// 初始数据为三个点 (0, 0) (80, 100) (400, 300) 
float[] pts = new float[]{0, 0, 80, 100, 400, 300};
// 构造一个matrix，x坐标缩放0.5
Matrix matrix = new Matrix();
matrix.setScale(0.5f, 1f);
// 输出pts计算之前数据
Log.i(TAG, "before: "+ Arrays.toString(pts));
// 调用map方法计算
matrix.mapPoints(pts);
// 输出pts计算之后数据
Log.i(TAG, "after : "+ Arrays.toString(pts));
//结果
//before: src=[0.0, 0.0, 80.0, 100.0, 400.0, 300.0]
//before: dst=[0.0, 0.0, 0.0, 0.0, 0.0, 0.0]
//after : src=[0.0, 0.0, 80.0, 100.0, 400.0, 300.0]
//after : dst=[40.0, 100.0, 200.0, 300.0, 0.0, 0.0]

2.float mapRadius (float radius):测量半径，由于圆可能会因为画布变换成椭圆，所以测量的是平均半径

float radius = 100;
float result = 0;
// 构造一个matrix，x坐标缩放0.5
Matrix matrix = new Matrix();
matrix.setScale(0.5f, 1f);
Log.i(TAG, "mapRadius: "+radius);
result = matrix.mapRadius(radius);
Log.i(TAG, "mapRadius: "+result);
//结果
//mapRadius: 100.0
//mapRadius: 70.71068

3.mapRect:测量矩形变换后的位置
（1）boolean mapRect (RectF rect)：测量rect并将测量结果放入rect中，返回值是判断矩形经过变换后是否仍为矩形。

RectF rect = new RectF(400, 400, 1000, 800);

// 构造一个matrix
Matrix matrix = new Matrix();
matrix.setScale(0.5f, 1f);
matrix.postSkew(1,0);

Log.i(TAG, "mapRadius: "+rect.toString());

boolean result = matrix.mapRect(rect);

Log.i(TAG, "mapRadius: "+rect.toString());
Log.e(TAG, "isRect: "+ result);

//结果,使用了错切，所以返回结果为false
//mapRadius: RectF(400.0, 400.0, 1000.0, 800.0)
//mapRadius: RectF(600.0, 400.0, 1300.0, 800.0)
//isRect: false

(2) boolean mapRect (RectF dst, RectF src) 测量src并将测量结果放入dst中，返回值是判断矩形经过变换后是否仍为矩形。

4.mapVectors：测量向量,类似mapPoints，唯一的区别就是mapVectors不会受到位移的影响。

void mapVectors (float[] vecs)
void mapVectors (float[] dst, float[] src)
void mapVectors (float[] dst, int dstIndex, float[] src, int srcIndex, int vectorCount)

float[] src = new float[]{1000, 800};
float[] dst = new float[2];

// 构造一个matrix
Matrix matrix = new Matrix();
matrix.setScale(0.5f, 1f);
matrix.postTranslate(100,100);

// 计算向量, 不受位移影响
matrix.mapVectors(dst, src);
Log.i(TAG, "mapVectors: "+Arrays.toString(dst));

// 计算点
matrix.mapPoints(dst, src);
Log.i(TAG, "mapPoints: "+Arrays.toString(dst));

//结果
//mapVectors: [500.0, 800.0]
//mapPoints: [600.0, 900.0]

5. 特殊方法

setPolyToPoly:poly全称是Polygon，多边形的意思

   boolean setPolyToPoly (
        float[] src,    // 原始数组 src [x,y]，存储内容为一组点
        int srcIndex,   // 原始数组开始位置
        float[] dst,    // 目标数组 dst [x,y]，存储内容为一组点
        int dstIndex,   // 目标数组开始位置
        int pointCount) // 测控点的数量 取值范围是: 0到4,setPolyToPoly最多可以支持4个点,这四个点通常为图形的四个角，可以通过这四个角将视图从矩形变换成其他形状

引用自http://www.gcssloop.com/customview/Matrix_Method

举个栗子

  //初始化
    private void initBitmapAndMatrix() {
        bitmap = BitmapFactory.decodeResource(getResources(), R.mipmap.bear);
        matrix = new Matrix();
        src = new float[]{0, 0, //左上角
                bitmap.getWidth(), 0,//右上角
                0, bitmap.getHeight(),//左下角
                bitmap.getWidth(), bitmap.getHeight()//右下角
        };
        dst = src.clone();
    }

    @Override
    public boolean onTouchEvent(MotionEvent event) {
        if (event.getAction() == MotionEvent.ACTION_MOVE) {
            float x = event.getX();
            float y = event.getY();
            // 根据触控位置改变dst
            for (int i = 0; i < 8; i = i + 2) {
                if (Math.abs(dst[i] - x) <= 150 && Math.abs(dst[i + 1] - y) <= 150) {
                    dst[i] = x - 100;  //canvas.translate(100, 100)，所以要-100
                    dst[i + 1] = y - 100;
                    break;
                }
            }
            invalidate();
        }
        return true;
    }

    @Override
    protected void onDraw(Canvas canvas) {
        super.onDraw(canvas);
        canvas.drawColor(Color.RED);
        canvas.translate(100, 100);
        matrix.reset();

        //将四个点的位置变换至dst的位置
        matrix.setPolyToPoly(src, 0, dst, 0, 4);
        //绘制图片
        canvas.drawBitmap(bitmap, matrix, null);
        //绘制四个点的位置
        for (int i = 0; i < 8; i = i + 2) {
            canvas.drawPoint(dst[i], dst[i + 1], paint);
        }
    }

效果如下：

至于1、2、3个点的效果，可以点击这里查看，这里就不讲解了，其实，一个点的话，就是只能控制一个点，额。

setRectToRect:将源矩形的内容填充到目标矩形中

boolean setRectToRect (RectF src,           // 源区域
                RectF dst,                  // 目标区域
                Matrix.ScaleToFit stf)      // 缩放适配模式

Matrix.ScaleToFit stf: ScaleToFit 是一个枚举类型，共包含了四种模式:
CENTER 居中，对src等比例缩放，将其居中放置在dst中。
START 顶部，对src等比例缩放，将其放置在dst的左上角。
END 底部，对src等比例缩放，将其放置在dst的右下角。
FILL 充满，拉伸src的宽和高，使其完全填充满dst。

举个栗子⤵️

 int width, height;
    @Override
    protected void onSizeChanged(int w, int h, int oldw, int oldh) {
        super.onSizeChanged(w, h, oldw, oldh);
        width = w;
        height = h;
    }
    @Override
    protected void onDraw(Canvas canvas) {
        super.onDraw(canvas);
        RectF src = new RectF(0, 0, bitmap.getWidth(), bitmap.getHeight());
        RectF dst = new RectF(100, 0, width - 100, height);
        //居中显示
        matrix.setRectToRect(src, dst, Matrix.ScaleToFit.CENTER);
        canvas.drawBitmap(bitmap, matrix, null);
    }

居中显示

3.rectStaysRect：判断矩形经过变换后是否仍为矩形
4.setSinCos：设置sinCos值，这个是控制Matrix旋转的，由于Matrix已经封装好了Rotate方法，所以这个并不常用

// 方法一
void setSinCos (float sinValue,     // 旋转角度的sin值
                float cosValue)     // 旋转角度的cos值

// 方法二
void setSinCos (float sinValue,     // 旋转角度的sin值
                float cosValue,     // 旋转角度的cos值
                float px,           // 中心位置x坐标
                float py)           // 中心位置y坐标

举个栗子：

       Matrix matrix = new Matrix();
        // 旋转90度
        // sin90=1
        // cos90=0
        matrix.setSinCos(1f, 0f);
        Log.i("rotation", "setSinCos:" + matrix.toShortString());

        // 重置
        matrix.reset();
        // 旋转90度
        matrix.setRotate(90);
        Log.i("rotation", "setRotate:" + matrix.toShortString());
//结果：
//setSinCos:[0.0, -1.0, 0.0][1.0, 0.0, 0.0][0.0, 0.0, 1.0]
//setRotate:[0.0, -1.0, 0.0][1.0, 0.0, 0.0][0.0, 0.0, 1.0]

5.其他方法
invert：求矩阵的逆矩阵
isAffine：判断当前矩阵是否为仿射矩阵，API21(5.0)才添加的方法。
isIdentity：判断当前矩阵是否为单位矩阵。

三.利用setPolyToPoly制造3D效果

点击进入⤵️
Android FoldingLayout 折叠布局原理及实现（一）
Android FoldingLayout 折叠布局原理及实现（二）

参考资料

官网
Matrix详解