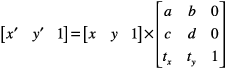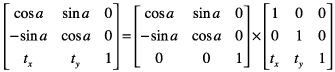Quartz 2D 编程指南五：变换

Transforms

The Quartz 2D drawing model defines two completely separate coordinate spaces: user space, which represents the document page, and device space, which represents the native resolution of a device. User space coordinates are floating-point numbers that are unrelated to the resolution of pixels in device space. When you want to print or display your document, Quartz maps user space coordinates to device space coordinates. Therefore, you never have to rewrite your application or write additional code to adjust the output from your application for optimum display on different devices.

Quartz 2D绘图模型定义了两个完全独立的坐标空间：表示文档页面的用户空间和表示设备的原始分辨率的设备空间。 用户空间坐标是与设备空间像素分辨率无关的浮点数。 当您要打印或显示文档时，Quartz将用户空间坐标映射到设备空间坐标。 因此，您不必重写应用程序或编写其他代码来调整应用程序的输出，以便在不同设备上进行最佳显示。

You can modify the default user space by operating on the current transformation matrix, or CTM. After you create a graphics context, the CTM is the identity matrix. You can use Quartz transformation functions to modify the CTM and, as a result, modify drawing in user space.

您可以通过使用当前转换矩阵或CTM来修改默认用户空间。 创建图形上下文后，CTM是单位矩阵。 您可以使用Quartz转换函数修改CTM，来修改用户空间中的绘图。

This chapter:

• Provides an overview of the functions you can use to perform transformations
• Shows how to modify the CTM
• Describes how to create an affine transform
• Shows how to determine if two transforms are equivalent
• Describes how to obtain the user-to-device-space transform
• Discusses the math behind affine transforms

本章：

• 概述可用于执行转换的函数
• 描述如何修改CTM
• 描述如何创建仿射变换
• 描述如何确定两个变换是否相等
• 描述如何获取用户到设备空间的变换
• 讨论仿射变换后的数学

1.About Quartz Transformation Functions(Quartz变换函数)

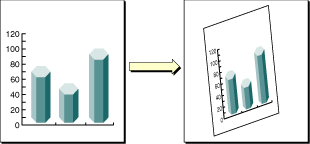
You can easily translate, scale, and rotate your drawing using the Quartz 2D built-in transformation functions. With just a few lines of code, you can apply these transformations in any order and in any combination. Figure 5-1 illustrates the effects of scaling and rotating an image. Each transformation you apply updates the CTM. The CTM always represents the current mapping between user space and device space. This mapping ensures that the output from your application looks great on any display screen or printer.

您可以使用Quartz 2D内置转换函数轻松地移动，缩放和旋转绘图。 只需几行代码，就可以以任何顺序和任意组合应用这些转换。 图5-1说明了缩放和旋转图像的效果。 您应用的每个转换都会更新CTM。 CTM总是表示用户空间和设备空间之间的当前映射。 此映射确保您的应用程序的输出在任何显示屏幕或打印机上看起来都很棒。

Figure 5-1 Applying scaling and rotation

The Quartz 2D API provides five functions that allow you to obtain and modify the CTM. You can rotate, translate, and scale the CTM, and you can concatenate an affine transformation matrix with the CTM. See Modifying the Current Transformation Matrix.

Quartz 2D API提供了五个函数，允许您获取和修改CTM。 您可以旋转，平移和缩放CTM，您可以将仿射变换矩阵与CTM连接起来。 请参阅修改当前转换矩阵。

Quartz also allows you to create affine transforms that don’t operate on user space until you decide to apply the transform to the CTM. You use another set of functions to create affine transforms, which can then be concatenated with the CTM. See Creating Affine Transforms.

Quartz还允许我们在决定将变换应用于CTM之前不对用户空间进行仿射变换。我们使用另一组函数来创建仿射变换，然后可以将其连接到CTM。参见创建仿射变换。

You can use either set of functions without understanding anything about matrix math. However if you want to understand what Quartz does when you call one of the transform functions, read The Math Behind the Matrices.

我们可以使用任何一组函数，而不必了解矩阵数学的任何内容。但是，如果您想了解Quartz在调用其中一个变换函数时会做什么，请阅读矩阵后面的数学。

2.Modifying the Current Transformation Matrix (修改当前坐标系)

You manipulate the CTM to rotate, scale, or translate the page before drawing an image, thereby transforming the object you are about to draw. Before you transform the CTM, you need to save the graphics state so that you can restore it after drawing. You can also concatenate the CTM with an affine transform (see Creating Affine Transforms). Each of these four operations—translation, rotation, scaling, and concatenation—is described in this section along with the CTM functions that perform each operation.

The following line of code draws an image, assuming that you provide a valid graphics context, a pointer to the rectangle to draw the image to, and a valid CGImage object. The code draws an image, such as the sample rooster image shown in Figure 5-2. As you read the rest of this section, you’ll see how the image changes as you apply transformations.

在绘制图像之前，您可以操纵CTM旋转，缩放或平移页面，从而转换要绘制的对象。 在转换CTM之前，需要保存图形状态，以便您可以在绘制后进行恢复。 您还可以将CTM与仿射变换相连（请参阅创建仿射变换）。 这四个操作中的每一个 - 平移，旋转，缩放和连接 - 在本节中将与执行每个操作的CTM功能一起进行描述。

以下代码行绘制一个图像，假设您提供了一个有效的图形上下文，一个指向矩形以将图像绘制到的指针，以及一个有效的CGImage对象。 代码绘制图像，如图5-2所示的公鸡图像。 当您阅读本节的其余部分时，您将看到在应用转换时图像的变化。

CGContextDrawImage (myContext, rect, myImage);

Figure 5-2 An image that is not transformed

Translation moves the origin of the coordinate space by the amount you specify for the x and y axes. You call the function CGContextTranslateCTM to modify the x and y coordinates of each point by a specified amount. Figure 5-3 shows an image translated by 100 units in the x-axis and 50 units in the y-axis, using the following line of code:
平移将坐标空间的原点移动到您为x轴和y轴指定的量。你调用函数CGContextTranslateCTM来修改每个点的x和y坐标指定的量。图5-3显示了使用以下代码行，在x轴上以100个单位转换的图像和y轴上的50个单位：

CGContextTranslateCTM (myContext, 100, 50);

Figure 5-3 A translated image

Rotation moves the coordinate space by the angle you specify. You call the function CGContextRotateCTM to specify the rotation angle, in radians. Figure 5-4 shows an image rotated by –45 degrees about the origin, which is the lower left of the window, using the following line of code:
旋转将坐标空间移动您指定的角度。您调用函数CGContextRotateCTM以弧度表示旋转角度。图5-4显示了一个关于原点旋转-45度的图像，它是窗口的左下角，使用以下代码行：

CGContextRotateCTM (myContext, radians(–45.));

The image is clipped because the rotation moved part of the image to a location outside the context. You need to specify the rotation angle in radians.
图像被剪裁，因为旋转将图像的一部分移动到上下文之外的位置。您需要以弧度表示旋转角度。
It’s useful to write a radians routine if you plan to perform many rotations.
如果您计划执行多次旋转，写一个弧度例程很有用。

#include 
static inline double radians (double degrees) {return degrees * M_PI/180;}

Figure 5-4 A rotated image

Scaling changes the scale of the coordinate space by the x and y factors you specify, effectively stretching or shrinking the image. The magnitude of the x and y factors governs whether the new coordinates are larger or smaller than the original. In addition, by making the x factor negative, you can flip the coordinates along the x-axis; similarly, you can flip coordinates horizontally, along the y-axis, by making the y factor negative. You call the function CGContextScaleCTM to specify the x and y scaling factors. Figure 5-5 shows an image whose x values are scaled by .5 and whose y values are scaled by .75, using the following line of code:
缩放通过您指定的x和y因子来更改坐标空间的比例，有效地拉伸或缩小图像。 x和y因子的大小决定新坐标是否大于或小于原始坐标。另外，通过使x因子为负，可以沿x轴翻转坐标;类似地，您可以通过使y因子为负值沿着y轴水平翻转坐标。您调用函数CGContextScaleCTM来指定x和y缩放因子。图5-5显示了一个图像，其x值以.5缩放，其y值用.75表示，使用以下代码行：

CGContextScaleCTM (myContext, .5, .75);

Figure 5-5 A scaled image

Concatenation combines two matrices by multiplying them together. You can concatenate several matrices to form a single matrix that contains the cumulative effects of the matrices. You call the function CGContextConcatCTM to combine the CTM with an affine transform. Affine transforms, and the functions that create them, are discussed in Creating Affine Transforms.
连接将两个矩阵相乘在一起。您可以连接几个矩阵以形成包含矩阵的累积效应的单个矩阵。您调用函数CGContextConcatCTM将CTM与仿射变换相结合。在创建仿射变换中讨论仿射变换和创建它们的功能。

Another way to achieve a cumulative effect is to perform two or more transformations without restoring the graphics state between transformation calls. Figure 5-6 shows an image that results from translating an image and then rotating it, using the following lines of code:
实现累积效果的另一种方法是执行两次或多次转换，而不会在转换函数调用时恢复图形状态。 图5-6显示了使用以下代码行转换图像，然后旋转图像的图像：

CGContextTranslateCTM (myContext, w,h);
CGContextRotateCTM (myContext, radians(-180.));

Figure 5-6 An image that is translated and rotated

Figure 5-7 shows an image that is translated, scaled, and rotated, using the following lines of code:

CGContextTranslateCTM (myContext, w/4, 0);
CGContextScaleCTM (myContext, .25,  .5);
CGContextRotateCTM (myContext, radians ( 22.));

Figure 5-7 An image that is translated, scaled, and then rotated

The order in which you perform multiple transformations matters; you get different results if you reverse the order. Reverse the order of transformations used to create Figure 5-7 and you get the results shown in Figure 5-8, which is produced with this code:
转换函数执行的顺序不同会产生不同的效果。

CGContextRotateCTM (myContext, radians ( 22.));
CGContextScaleCTM (myContext, .25,  .5);
CGContextTranslateCTM (myContext, w/4, 0);

Figure 5-8 An image that is rotated, scaled, and then translated

3.Creating Affine Transforms(创建仿射变换)

The affine transform functions available in Quartz operate on matrices, not on the CTM. You can use these functions to construct a matrix that you later apply to the CTM by calling the function CGContextConcatCTM. The affine transform functions either operate on, or return, a CGAffineTransform data structure. You can construct simple or complex affine transforms that are reusable.

Quartz中的仿射变换函数可用于矩阵，而不是在CTM上。 您可以使用这些函数构造一个矩阵，以便您以后通过调用函数CGContextConcatCTM将其应用于CTM。 仿射变换函数可以操作或返回CGAffineTransform数据结构。 您可以构建可重用的简单或复杂的仿射变换。

The affine transform functions perform the same operations as the CTM functions—translation, rotation, scaling, and concatenation. Table 5-1 lists the functions that perform these operations along with information on their use. Note that there are two functions for each of the translation, rotation, and scaling operations.

仿射变换函数执行与CTM功能相同的操作 - 平移，旋转，缩放和连接。 表5-1列出了执行这些操作的功能及其使用信息。 请注意，每个平移，旋转和缩放操作都有两个函数。

Table 5-1 Affine transform functions for translation, rotation, and scaling

Function	Use
CGAffineTransformMakeTranslation	To construct a new translation matrix from x and y values that specify how much to move the origin.
CGAffineTransformTranslate	To apply a translation operation to an existing affine transform.
CGAffineTransformMakeRotation	To construct a new rotation matrix from a value that specifies in radians how much to rotate the coordinate system.
CGAffineTransformRotate	To apply a rotation operation to an existing affine transform.
CGAffineTransformMakeScale	To construct a new scaling matrix from x and y values that specify how much to stretch or shrink coordinates.
CGAffineTransformScale	To apply a scaling operation to an existing affine transform.

Quartz also provides an affine transform function that inverts a matrix, CGAffineTransformInvert. Inversion is generally used to provide reverse transformation of points within transformed objects. Inversion can be useful when you need to recover a value that has been transformed by a matrix: Invert the matrix, and multiply the value by the inverted matrix, and the result is the original value. You usually don’t need to invert transforms because you can reverse the effects of transforming the CTM by saving and restoring the graphics state.

Quartz还提供了一个仿射变换函数，它反转矩阵CGAffineTransformInvert。反转通常用于提供变换对象内的点的反向变换。当您需要恢复由矩阵变换的值时，反转可能很有用：反转矩阵，并将该值乘以反向矩阵，结果为原始值。您通常不需要反转转换，因为您可以通过保存和恢复图形状态来扭转转换CTM的效果。

In some situations you might not want to transform the entire space, but just a point or a size. You operate on a CGPoint structure by calling the function CGPointApplyAffineTransform. You operate on a CGSize
structure by calling the functionCGSizeApplyAffineTransform. You can operate on a CGRect structure by calling the function CGRectApplyAffineTransform. This function returns the smallest rectangle that contains the transformed corner points of the rectangle passed to it. If the affine transform that operates on the rectangle performs only scaling and translation operations, the returned rectangle coincides with the rectangle constructed from the four transformed corners.

在某些情况下，您可能不想要转换整个空间，而只是一点或一个大小。您可以通过调用CGPointApplyAffineTransform函数在CGPoint结构上运行。您在CGSize上操作
结构通过调用functionCGSizeApplyAffineTransform。您可以在CGRect上操作
结构通过调用函数CGRectApplyAffineTransform。此函数返回包含传递给它的矩形的变换角点的最小矩形。如果在矩形上操作的仿射变换仅执行缩放和平移操作，返回的矩形与由四个变换的角构成的矩形重合。

You can create a new affine transform by calling the function CGAffineTransformMake, but unlike the other functions that make new affine transforms, this one requires you to supply matrix entries. To effectively use this function, you need to have an understanding of matrix math. See The Math Behind the Matrices.

您可以通过调用函数CGAffineTransformMake来创建一个新的仿射变换，但是与其他进行新仿射变换的函数不同，这需要您提供矩阵项。要有效地使用此功能，您需要了解矩阵数学。见矩阵背后的数学。

4.Evaluating Affine Transforms(评价仿射变换)

You can determine whether one affine transform is equal to another by calling the function CGAffineTransformEqualToTransform. This function returns true if the two transforms passed to it are equal and false otherwise.

您可以通过调用函数CGAffineTransformEqualToTransform来确定一个仿射变换是否等于另一个。 如果传递给它的两个变换相等，则此函数返回true，否则返回false。

The function CGAffineTransformIsIdentity is a useful function for checking whether a transform is the identity transform. The identity transform performs no translation, scaling, or rotation. Applying this transform to the input coordinates always returns the input coordinates. The Quartz constant CGAffineTransformIdentity represents the identity transform.

函数CGAffineTransformIsIdentity是检查变换是否是标识变换的有用函数。 标识转换不会执行任何平移，缩放或旋转。 将此变换应用于输入坐标始终返回输入坐标。 Quartz常量CGAffineTransformIdentity表示身份转换。

5.Getting The User to Device Space Transform(获取用户空间到设备空间的转换)

Typically when you draw with Quartz 2D, you work only in user space. Quartz takes care of transforming between user and device space for you. If your application needs to obtain the affine transform that Quartz uses to convert between user and device space, you can call the function CGContextGetUserSpaceToDeviceSpaceTransform.

通常当您使用Quartz 2D绘图时，只能在用户空间中工作。 Quartz负责为您转换用户和设备空间。如果您的应用程序需要获得Quartz用于在用户和设备空间之间转换的仿射变换，则可以调用函数CGContextGetUserSpaceToDeviceSpaceTransform。

Quartz provides a number of convenience functions to transform the following geometries between user space and device space. You might find these functions easier to use than applying the affine transform returned from the functionCGContextGetUserSpaceToDeviceSpaceTransform.

• Points. The functions CGContextConvertPointToDeviceSpace and CGContextConvertPointToUserSpace
  transform a CGPoint data type from one space to the other.
• Sizes. The functions CGContextConvertSizeToDeviceSpace and CGContextConvertSizeToUserSpace
  transform a CGSize data type from one space to the other.
• Rectangles. The functions CGContextConvertRectToDeviceSpace and CGContextConvertRectToUserSpace
  transform a CGRect data type from one space to the other.

Quartz提供了许多方便的功能，用于在用户空间和设备空间之间转换以下几何。您可能会发现这些函数比应用从函数CGContextGetUserSpaceToDeviceSpaceTransform返回的仿射变换更容易使用。

• 点。函数CGContextConvertPointToDeviceSpace和CGContextConvertPointToUserSpace将CGPoint数据类型从一个空间转换到另一个空间。
• 大小。函数CGContextConvertSizeToDeviceSpace和CGContextConvertSizeToUserSpace将CGSize数据类型从一个空间转换到另一个空间。
• 矩形。函数CGContextConvertRectToDeviceSpace和CGContextConvertRectToUserSpace将CGRect数据类型从一个空间转换到另一个空间。

6.The Math Behind The Matrices(矩阵背后的数学)

The only Quartz 2D function for which you need an understanding of matrix math is the function CGAffineTransformMake, which makes an affine transform from the six critical entries in a 3 x 3 matrix. Even if you never plan to construct an affine transformation matrix from scratch, you might find the math behind the transform functions interesting. If not, you can skip the rest of this chapter.

您需要了解矩阵数学的唯一Quartz 2D函数是CGAffineTransformMake的函数，该函数从3 x 3矩阵中的六个关键条目进行仿射变换。 即使你从未计划从头构建一个仿射变换矩阵，你可能会发现变换函数背后的数学有趣。 如果没有，可以跳过本章的其余部分。

The six critical values of a 3 x 3 transformation matrix —a, b, c, d, tx and ty— are shown in the following matrix:
3×3变换矩阵-a，b，c，d，tx和ty-的六个临界值如下列所示：

Note: The rightmost column of the matrix always contains the constant values 0, 0, 1. Mathematically, this third column is required to allow concatenation, which is explained later in this section. It appears in this section for the sake of mathematical correctness only.
注意：矩阵的最右边的列始终包含常量值0，0，1。数学上，这个第三列是允许连接所必需的，这在本节稍后解释。 为了数学正确性，它出现在本节中。

Given the 3 x 3 transformation matrix described above, Quartz uses this equation to transform a point (x, y) into a resultant point (x’, y’):

The result is in a different coordinate system, the one transformed by the variable values in the transformation matrix. The following equations are the definition of the previous matrix transform:

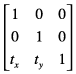
The following matrix is the identity matrix. It performs no translation, scaling, or rotation. Multiplying this matrix by the input coordinates always returns the input coordinates.

Using the formulas discussed earlier, you can see that this matrix would generate a new point (x’, y’) that is the same as the old point (x, y):

This matrix describes a translation operation:

These are the resulting equations that Quartz uses to apply the translation:

This matrix describes a scaling operation on a point (x, y):

These are the resulting equations that Quartz uses to scale the coordinates:

This matrix describes a rotation operation, rotating the point (x, y) counterclockwise by an angle a:

These are the resulting equations that Quartz uses to apply the rotation:

This equation concatenates a rotation operation with a translation operation:

These are the resulting equations that Quartz uses to apply the transform:

Note that the order in which you concatenate matrices is important—matrix multiplication is not commutative. That is, the result of multiplying matrix A by matrix B does not necessarily equal the result of multiplying matrix B by matrix A.
请注意，连接矩阵的顺序是重要的 - 矩阵乘法不可交换。也就是说，将矩阵A乘以矩阵B的结果不一定等于矩阵B乘以矩阵A的结果。

As previously mentioned, concatenation is the reason the affine transformation matrix contains a third column with the constant values 0, 0, 1. To multiply one matrix against another matrix, the number of columns of one matrix must match the number of rows of the other. This means that a 2 x 3 matrix cannot be multiplied against a 2 x 3 matrix. Thus we need the extra column containing the constant values.
如前所述，连接是仿射变换矩阵包含具有常数值0,0,1的第三列的原因。为了将一个矩阵与另一个矩阵相乘，一个矩阵的列数必须与另一个矩阵的行数相匹配。这意味着2×3矩阵不能与2×3矩阵相乘。因此，我们需要包含常量值的额外列。

An inversion operation produces original coordinates from transformed ones. Given the coordinates (x, y), which have been transformed by a given matrix A to new coordinates (x’, y’), transforming the coordinates (x’, y’) by the inverse of matrix A produces the original coordinates (x, y). When a matrix is multiplied by its inverse, the result is the identity matrix.
反演操作从转换的操作产生原始坐标。给定已经由给定矩阵A变换为新坐标（x'，y'）的坐标（x，y），将坐标（x'，y'）转换为矩阵A的倒数产生原始坐标（ x，y）。当矩阵乘以其逆时，结果是单位矩阵。