《Spectral–Spatial Classification of HyperspectralImagery with 3D Convolutional Neural Network》
摘要 - 最近的研究表明:使用空间-光谱信息可以提高HSI分类的准确度。HSI数据是一个3D立方体,3D空间滤波器是一个同时提取空间-光谱特征的有效方法。本文提出了一个3-D CNN的模型,不需要任何的数据预处理和后续处理,而且需要的参数量也很小。所以此方法轻量级、易训练、不会过拟合。和SAE、DBN、2-D CNN等方法做出比较,取得了很好的效果。
1. Introduction
高光谱传感器生成的HSI包含大量的空间-光谱信息,丰富的光谱信息是非常有用的。传统的HSI分类方法都是只利用光谱信息,这些方法都会面临一个问题“small - sample probem”:对于HSI的数百个光谱带来说,可能没有足够数量的训练样本。也就是说高维数据 和 有限的训练样本 的矛盾。这种矛盾现象叫做Hughes Phenomenon(休斯现象)。在HSI中有些光谱带是高度相关的,也就有了光谱带的冗余。而且只是提取光谱信息而不能提取重要的空间变化,会导致分类的精度性能不高。
为了提高分类性能,一个想法就是设计使用一个光谱-空间信息的分类器:将空间结构纳入像素级分类器中。空间信息提供了额外的有关形状、大小等可判别信息。
光谱-空间分类方法大致可以分为两类:
- 分别提取光谱、空间上下文信息
- 同时提取光谱和空间信息
1.1 分别提取特征
也就是说:利用多种空间滤波器提取空间依赖关系,然后将这些变换后的空间特征与光谱特征相结合,并在适当的时候应用降维进行像素级分类。后续处理可以通过马尔科夫随机场、graph cut等正则化方法对分类结果进行细化;还可以通过Hopfield 神经网络、模拟退火算法等优化算法进行提取光谱-空间特征。
1.2 同时提取光谱-空间特征
第二类通常是将空间信息与光谱特征结合起来,产生联合特征。例如,在高光谱数据上应用一系列不同尺度和频率产生的三维小波滤波器[23]、三维Gabor滤波器[24]或三维散射小波滤波器[25],提取光谱空间组合特征。同样,降维(DR)技术可以在保留判别信息的同时提取低维谱空间特征。由于HSI数据通常以三维数据集的形式呈现,第二种方法可以生成大量的特征,其中包含关于局部信号在空间、频谱和空间-频谱相关性方面的重要信息,这对于提高性能至关重要。
深度学习技术能够从原始输入数据中自动学习层次特性(从低级到高级),而不是依赖于手工设计的浅层特性:
- SAE/DBN:SAE和DBN以分层训练的方式提取深度特征。但是而由图像块patch组成的训练样本必须被伸展(Flatten)成到一维数据,才能满足模型的输入要求。伸展成一维的训练样本不能保留原始图像的空间信息。此外,SAE和DBN是无监督的,在学习特征时不直接使用标签信息。
- CNN-Based:基于cnn的模型具有检测局部特征的能力,而这些局部特征能够实现很好的分类性能。利用原始HSI数据的前几个主成分,2-D CNN可以提取空间特征。但是应用2-D CNN的时候,需要对原始输入图像进行PCA处理,将训练的HSI数据缩减到可控范围。由于空间特征和光谱特征是分开提取的,它们可能不能充分利用空间/光谱联合相关信息,而这对于分类是很重要的。
主成分分析(Principal Component Analysis,PCA), 是一种统计方法。通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量,转换后的这组变量叫主成分。
主成分分析的原理是设法将原来变量重新组合成一组新的相互无关的几个综合变量,同时根据实际需要从中可以取出几个较少的总和、变量尽可能多地反映原来变量的信息的统计方法叫做主成分分析或称主分量分析,也是数学上处理[降维]
本文提出了一种应用3D-CNN实现HSI分类的新方法。将3D 卷积核应用到三维HSI中,3D-CNN可以学习特征立方体的空间和频谱维数的局部信号变化,同时提取光谱特征和空间特征,充分利用了三维HSI数据的结构特征。
3-D CNN 一开始是应用在基于视频的应用,比如行人检测,他们的目的主要是学习时间-空间特征。相比之下,我们的方法采用光谱带作为输入,将光谱维度作为第三维,而且该方法不需要对原始HSI做任何预处理或后处理,直接以端到端方式进行训练,而且参数量大大减少。
2. Proposed Method
在采用2D-CNN进行特征提取和分类之前,通常采用DR方法降低光谱维数。
- 在[33]中,首先用PCA从HSI中提取前三个主成分(PCs),然后用2D-CNN从窗口大小为42 * 42的压缩HSI中提取深度特征,预测每个像素的标签。
- 采用随机PCA (R-PCA)沿谱维对整个HSI在[34]中进行压缩,保留前10 ~ 30个PCs。这是在2D-CNN被用来从压缩的HIS中提取深度特征(窗口大小为5 * 5)之前进行的,然后完成分类任务。
- [35]中提出的方法需要三个计算步骤:首先用2D-CNN提取高层特征,其中使用PCA算法对整个HSI进行降维,保留几个顶部波段;然后应用稀疏表示技术进一步减少第一步生成的高层空间特征。只有经过这两个步骤,才能得到基于学习稀疏字典的分类结果。
- Yue, J.; Zhao, W.; Mao, S.; Liu, H. Spectral-spatial classification of hyperspectral images using deep
convolutional neural networks. Remote Sens. Lett. 2015, 6, 468–477.- Makantasis, K.; Karantzalos, K.; Doulamis, A.; Doulamis, N. Deep supervised learning for hyperspectral data
classification through convolutional neural networks. In Proceedings of the IEEE International Geoscience
and Remote Sensing Symposium, Milan, Italy, 26–31 July 2015; pp. 4959–4962.- Liang, H.; Li, Q. Hyperspectral imagery classification using sparse representations of convolutional neural
network features. Remote Sens. 2016, 8.
以上这些方法的一个明显缺点是不能很好地保存光谱信息,由此提出了3-D CNN。
2-D vs. 3-D卷积的对比,戳此连接
总结:
- 2-D CNN -> 输出是2D -> 丧失大量的光谱信息
- 3-D CNN -> 输出的是3D cube -> 保存了光谱信息
3. 本篇论文网络架构
传统的卷积网络是由卷积+池化,堆叠模块组成。但是本片文章中所提出来的架构,只有两层卷积层,没有池化层,再加一层全连接层。
其不加池化层的原因是:池化层会降低HSI中的空间分辨率。
本文提出的3D-CNN模型有两个三维卷积层(C1和C2)和一个全连接层(F1)。根据二维CNN[1]的研究结果,3 * 3的卷积核的小接受域与较深的结构通常产生更好的结果。Tran等人也证明了小的3 * 3 * 3核是三维CNN学习[2]时空特征的最佳选择。受此启发,我们将三维卷积核的空间大小固定为3 * 3,同时只稍微改变了核的光谱深度。
卷积层的数量受输入样本(或图像立方体)的空间大小的限制,在本工作中,根据经验将窗口设置为5 * 5。使用空间大小为3 * 3的卷积核,进行两次卷积运算,将样本的大小减小到1 * 1。因此,所提出的3D-CNN只包含两个卷积层就足够了。此外,第二卷积层的核数设置为第一卷积层核数的两倍。
在每个三维卷积层上,将输入数据与可学习的三维核进行卷积;然后通过所选的激活函数运行卷积结果。将F1层的输出反馈给一个简单的线性分类器(如softmax),生成所需的分类结果。注意,网络使用标准的反向传播(BP)算法进行训练。本文以softmax损失为损失函数,对分类器进行训练。
将运行过程分为3部分:
- 训练样本(图像立方体)提取。提取S * S * L图像立方体,并将这些立方体的中心像素的类别标签作为训练样本。S * S为空间大小(窗口大小),L为光谱带数。
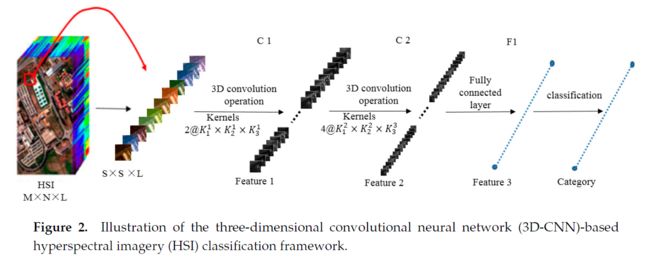
- 基于3D-CNN的深度光谱-空间特征提取。使用大小为S * S * L的样本作为输入数据。第一个三维卷积层C1包含两个三维核,每个核大小为,生成两个三维数据立方体。每个3-D CNN 卷积核生成一个3D数据立方体。将C1生成的两个三维数据立方体的作为输入,第二个3-D卷积层涉及四个3-D内核,并产生8个三维数据立方体(特征向量)。八个三维数据立方体被伸展的成一个特征向量,喂入到全连接层F1,其中输出特征向量(图2中称为特征3)包含最终学习到的深光谱空间特征。
- 基于深光谱空间特征的分类。我们使用softmax loss来训练分类器。与2D-CNN一样,使用随机梯度下降和反向传播来减小网络的损失。
4. 特征分析
在本节中,我们将说明所提出的3D-CNN提取了哪些特征。以HSI Pavia University场景为例,通过3D-CNN的不同图层,将学习到的特征可视化。香港西帕维亚大学有103个光谱。从原始HSI中提取一个大小为50 * 50 * 103的数据立方体,然后随机选取该数据立方体的四个波段,如图3a所示。与第一卷积层进行三维卷积运算后,将数据立方体转换为两个数据立方体,每个数据立方体的空间尺寸为48 * 48,选取8个波段,如图3b所示。将第一个卷积层的输出作为第二个卷积层的输入,从第二个卷积层的输出中提取8个波段,如图3c所示。
- 不同的对象类型激活不同的特征图像。例如,图3c中的八个特征图像基本上是由八个不同的内容激活的。
- 不同的层编码不同的特征类型。在较高的层,计算的特征更加抽象和可区分。
特征图数量规模巨大,其可看作输入图像的高级表示,一系类特征图组合起来才能获得一副图片的所有信息。
5. 数据以及参数问题
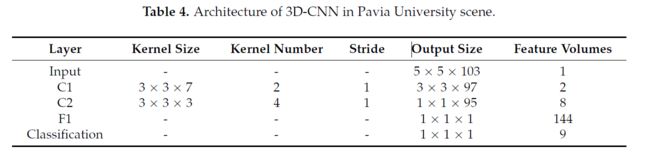
- Pavia University Scene -> 103个band -> 9类
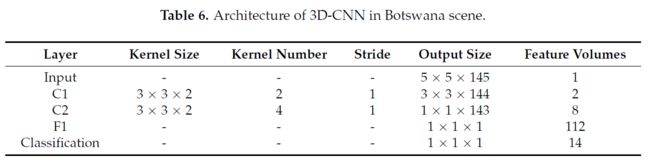
- Botswana Scene -> 145个band -> 14类
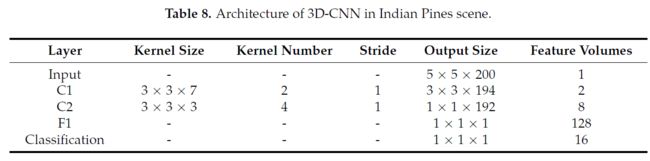
- Indian Pines Scene -> 200个band -> 16个类
3D-CNN经过10万多次迭代训练,每次迭代随机抽取20个样本。
Pavia University scene
Botswana Scene
Indian Pines Scene
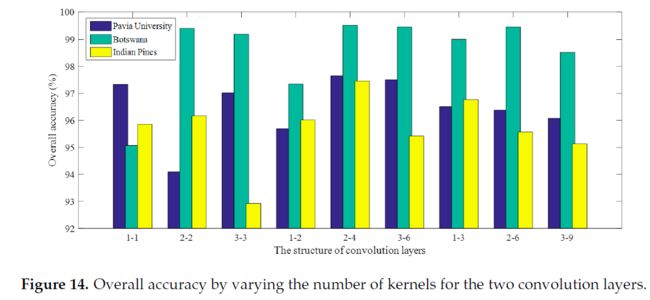
卷积核数量对性能的影响
由上图看出,C1层2个,C2层4个的最终性能是最好的。
3-D卷积核光谱深度的影响
[1]结果表明,3 * 3的卷积核的小接受域与较深的结构可以产生较好的结果。因此,对于所有这三个数据集,我们将三维内核的空间大小固定为3 * 3,C1和C2的内核数量分别为2和4。最后,我们改变了三维内核的光谱深度,从2到11,以确定一个精度最好的光谱深度。通过对训练样本的交叉验证实验,确定果仁的光谱深度设置如下:对于Pavia University和Indian pine场景,C1和C2分别设置为7和3。在Botswana scene的场景中,C1和C2内核的光谱深度都设置为2。
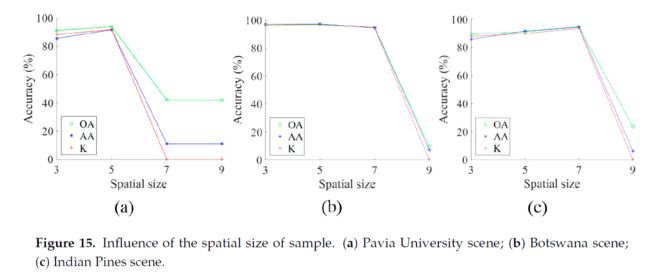
训练样本的窗口大小的影响
为了找到训练样本的最佳窗口大小,我们还通过提取不同大小的光谱空间特征来测试模型, 和
一般来说,目标像素及其相邻像素属于同一类。利用邻域信息提取的光谱空间特征通常有助于降低类内方差,从而有助于提高分类性能。然而,过大的窗口区域可能会产生额外的噪声,特别是当像素位于一个类别的边缘时。通过以上在这三个数据集中实验的对比,使得最后准确度最高的窗口大小为 。
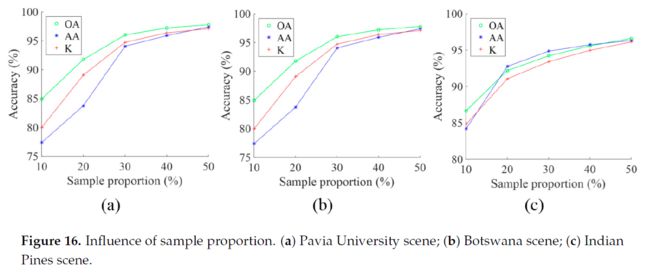
训练样本规模的影响
通过上图得出的结论:对于Pavia University dataset用30%的数据作为训练数据;对于Botswana scene 和 Indian Pines scene数据集用40%的数据作为训练数据可达到最好性能。
6. 讨论 + 未来展望
- CNN-Based的实验性能比 SAE\DBN的实验性能要好,在SAE\DBN中,其生成的特征向量需要伸展成一维向量,以满足这两种网络的输入格式。但是伸展为一维向量的话,会导致位置信息的丢失。而且SAE\DBN是一种无监督的学习方式,不能够很好的利用图像的标签数据。
- 3-D CNN可以提取挂光谱-空间信息;1-D CNN可以提取光谱特征;2-D CNN 可以提取空间特征。而且使用3-D 卷积核可以直接对HSI这种高维数据进行卷积,无需任何预处理和后续处理,在SAE、DBN中,PCA需要对HSI数据进行降维到一个可以接受的水平。
- 3D-CNN包含较少的参数,而且很容易收敛。
在HSI中,无标签样本要比标签样本获取容易,无监督或者半监督的分类方式是更
参考文献:
-
Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition.In Proceedings of the International Conference on Learning Representations, San Diego, CA, USA,7–9 May 2015. ↩ ↩
-
Tran, D.; Bourdev, L.; Fergus, R.; Torresani, L.; Paluri, M. Learning spatiotemporal features with 3D convolutional networks. In Proceedings of the 2015 IEEE International Conference on Computer Vision,Santiago, Chile, 7–13 December 2015; pp. 7–13. ↩