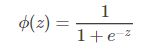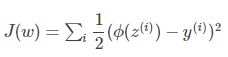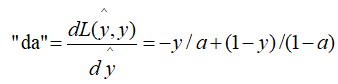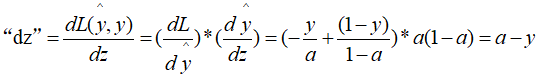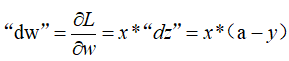2.1 二分类Binary Classification
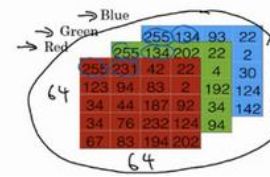
图1 图2
一张64*64像素的图片如图1，在计算机中保存形式如图2所示。三个64*64的矩阵，分别对应图片中红、黄、蓝三种像素的强度值。我们把这些像素值提取出来放到一个特征向量x，而x的总维度nx将是64*64*3=12288。二分类问题中，我们的目标就是以图片的特征向量作为输入，然后预测输出结果y是1还是0，即图片中有猫还是没猫。
nx：输入特征向量的维度，有时直接用n表示；
m：表示训练样本数，有时用Mtarin:表示训练集样本数，Mtest表示测试集样本数；
x：表示一个nx维数据，为输入数据，维度（nx, 1）；
y：表示输出结果，取值（0, 1）；
(x(i), y(i))：表示第i组训练数据；
X = [x(1), x(2), ... ,x(m)]：1*m的矩阵，表示所有训练数据集的输入值；
Y = [y(1), y(2), ... ,y(m)]：1*m的矩阵，表示所有训练数据集的输出值；
2.2逻辑回归函数
对于上面的二分类问题，你想要一个算法能够输出预测，表示为z，也就是对实际值y的估计，或者说表示实际值y等于1的概率。我们很容易想到用线性回归模型得到这个算法
但是这个函数的输出z不在{0，1}。这时候我们需要一个算法来归一化z值，使得z满足
然而该函数不连续，我们希望有一个单调可微的函数来供我们使用，于是便找到了Sigmoid 函数来替代。
两个函数的曲线图如下所示
2.3 逻辑回归的损失函数
损失函数又称误差函数，用来衡量预测输出值和实际值有多接近。Loss function：L(y^, y)。
从上节我们得到逻辑回归的输出函数：
上标（i）用来区分索引和样本，y^或者ϕ(z(i))表示训练样本i对应的预测值。
得到上面的两个函数，接下来要根据给定的训练集，把参数w和b给求出来。要找参数w和b，首先就是得把代价函数（cost function）给定义出来，也就是损失函数。
我们第一个想到的自然是模仿线性回归的做法，利用误差平方和来当损失函数。
i表示第i个样本点，y(i)表示第i个样本的真实值，ϕ(z(i))表示第i个样本的预测值。
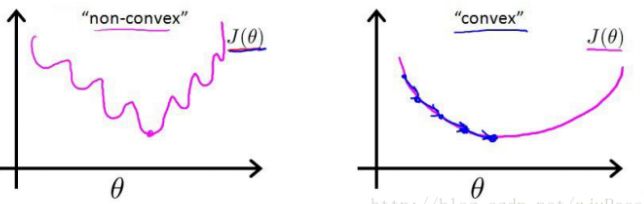
但是该函数是一个非凸函数，这就意味着代价函数有着许多的局部最小值，这不利于我们的求解。
逻辑回归中用到的损失函数是：
当y=1时，y^会无限接近于1；当y=0时，y^会无限接近于0。
算法的代价函数是对于m个样本的损失函数求和然后除以m：
2.4 梯度下降
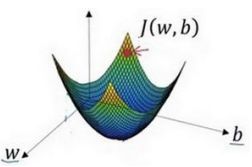
梯度下降可以在你的测试集上，通过最小化代价函数（成本函数）J(w, b)来训练参数w和b。上面这个图中，横轴表示空间参数w和b，代价函数J（w, b）是在水平轴w和b上的曲面，因此曲面高度就是J（w, b）在某一点的函数值。我们要做的就是找到使得代价函数J（w, b）函数值最小时，对应参数w和b。
w和b的运算公式：
：= 表示更新参数
：就是函数J（w, b）对w求导，代码中用dw表示；
：就是函数J（w, b）对b求导，代码中用db表示；
a：表示学习率，用来控制步长。
2.9 逻辑回归中的梯度下降
逻辑回归公式：
损失函数公式：
代价函数公式：
参数w、b的更新公式：
a.根据损失函数计算L(y^, y)关于y^的导数：
b..根据损失函数计算L(y^, y)关于z的导数：
c.根据损失函数计算L(y^, y)关于w的导数：
d.根据损失函数计算L(y^, y)关于b的导数：
“db” = "dz" = a-y
e.更新参数w和b
w = w - a * “dw” （a：学习率）
b = b - a * “db”
2.10 m个样本的梯度下降
