卷积神经网络中重要的基础知识汇总

说明：以下内容主要参考：

https://zhuanlan.zhihu.com/p/44257514

https://zhuanlan.zhihu.com/p/27908027

https://zhuanlan.zhihu.com/p/28173972

https://blog.goodaudience.com/artificial-neural-networks-explained-436fcf36e75

输入层

CNN的输入层主要是 n x m x 3 的RGB图像。（在代码中，输入通常是以的形式输入的，其中的代表batch_size，代表channel，和分别是图像的高和宽。）

卷积层

计算输入图像和卷积核之间的卷积。

输出图像的宽度：

输出图像的高度：

其中，W和H是原图像的宽和高，和是卷积核的宽和高，P是padding，S是步长。

为什么要先使用卷积层？

答：（1）一方面，卷积层提供了一种稀疏连接。传统的神经网络使用矩阵乘法来建立输入与输出之间的连接关系，输入与输出是全相连的，这会导致很大的运算量，当数据集较大时（如要训练几千万甚至上亿张图片），这基本是不现实的。而CNN提供了解决这个问题的一种思路：卷积核的大小通常远小于输入尺寸的大小，而每次参与运算的仅仅是图片上与卷积核对应的那一部分区域，因此与全连接网络相比，卷积层极大地减小了运算量；

注意：对于输入的每个通道，输出每个通道上的卷积核是不一样的。如果输入是192 x 28 x 28（其中的192是通道数），卷积核的尺寸是128 x 3 x 3，那么卷积的参数一共有192 x 128 x 3 x 3。

注意：卷积核的权值共享只在每个单独的通道上有效，而通道和通道之间对应的卷积核是相互独立的（不参与权值共享）。

（2）另一方面，卷积核实现了参数共享，这可以减少模型需要计算和存储的参数数量，从而降低了模型的存储需求，提高了模型的运算效率。

局部连接与参数共享是CNN最重要的两个性质。

问题1：CNN中为什么会有 1 x 1 的卷积层？它在网络中起什么作用？

参考：https://zhuanlan.zhihu.com/p/40050371

答：1 x 1卷积核又称为“Network in Network”，它可以看成是一种“全连接”。但注意，这里的“全连接”和CNN最后的全连接层并不完全一样，它们的功能是类似的（全连接层可以实现的，1 x 1卷积核也可以实现），但是由于卷积层参数共享的特点，使用1 x 1卷积核实现的全连接只需要更少的参数（而全连接层需要大量的参数），因此在某些需要追求运算速度的场合，CNN最后几层的全连接层完全可以用1 x 1的卷积层代替。

需要注意的是，1 x 1卷积一般只改变输出通道数（channel），而不改变输出的宽度和高度。

1 x 1卷积核的作用有以下三点：

降维/升维：

如果卷积核的channel数大于输入的channel数，则会对输入进行升维；反之，会对输入进行降维。
增加非线性：

1 x 1卷积核可以在保持feature map尺度不变（即不损失分辨率）的前提下大幅增加非线性特性（利用后面的非线性激活函数），把网络做的很deep。
跨通道信息交互（channel的变换）：

使用 1 x 1卷积核，实现升维和降维的操作其实就是channel间信息的线性组合变换。3 x 3， 64 channels的卷积核后面添加一个1 x 1，28 channels的卷积核，就变成了3 x 3，28 channels 的卷积核，原来的64个channels就可以理解为跨通道线性组合变成了28 channels，这就是通道间的信息交互。（注意：这里只是在channel维度上做线性组合。）

问题2：输入图像和卷积核之间的卷积运算具体是如何实现的？在主流的深度学习框架中，conv层的底层实现机制是什么？

答：是将卷积转化为矩阵乘法来实现的（如将卷积核转化为一个矩阵，然后将卷积核对应窗口内的图像转化为另一个矩阵）。

caffe中卷积运算的原理可以参考：https://blog.csdn.net/qianqing13579/article/details/71844172

tensorflow和pytorch中卷积的实现方法可以参考：https://zhuanlan.zhihu.com/p/46305636

在tensorflow中，是将filter展开成大小为：

的二维矩阵，然后从input tensor中按照每个filter位置上提取图像patches来构成一个大小为：

的tensor。然后，对每个patch，右乘filter matrix，即可得到最终的输出：

问题3：CNN中的channel是如何变化的？

答：强烈建议参考：https://blog.csdn.net/sscc_learning/article/details/79814146

假设卷积的过程是：input * filter = feature map，其中input有一个channels（如原始的输入图片可能有RGB三个通道），不妨记为in_channels（这里以in_channels = 3为例）。为了使这个卷积过程能够运算，filter就需要包含4个维度：首先是卷积核的H和W，不再赘述；其次，卷积核必须有in_channels层（如果考虑刚才的in_channels = 3，则这里卷积核必须有3层），因为input的每一层都需要有一层卷积核去跟它进行卷积，因此input和filter在“层”这个维度上必须匹配。这样卷积后将会得到3层，而这3层对应位置的元素相加后才能得到最终的feature map，而且这个最终的feature map只有一层（即一个通道）。

如果想让最终的feature map有多个通道，那就不能只用一个卷积核。注意，这里用的量词是“个”，一“个”卷积核可能包括很多层。假如我们这里用了32个卷积核，根据刚才的讨论，每一个包含3层的卷积核最终只能产生1个通道的feature map，那么现在32个卷积核就可以产生32个通道的feature map，至此，卷积后输出的feature map的channel数已经从输入的in_channels = 3变成了out_channels = 32。

注意：在调用深度学习框架时，卷积核的层数通常不指定（框架会根据前面一层的输出通道设定）。

池化层

池化函数使用某一区域内的总体特征来代替网络在该位置的输出。包括max pooling和average pooling，前者使用最多。

为什么要池化？

Pooling is performed in neural networks to reduce variance and computation complexity.

对空间区域进行池化能够产生平移不变性（即当我们对输入进行少量平移时，经过池化函数后的大多数输出并不会发生改变），“空间位置上的最大池化对于平移是天然不变的”。池化后参数会减少，这有助于提高计算效率并减少对于参数的存储需求。

问题1：max pooling 和 average pooling 的区别是什么？

参考：https://blog.csdn.net/u012193416/article/details/79432668

https://medium.com/@bdhuma/which-pooling-method-is-better-maxpooling-vs-minpooling-vs-average-pooling-95fb03f45a9

首先，max pooling是取对应区域中的最大值，average pooling是取对应区域中所有数字的平均值。

其次，没有哪一种池化方法是最好的，这要取决于我们拥有的数据以及我们想要从数据中提取的特征。

但是，通常来讲max pooling的效果更好，虽然max pooling和average pooling都对数据做了下采样，但max pooling感觉更像是做了特征选择，选出了分类辨识度更好的特征，提供了非线性。（在早先的CNN架构中，average pooling是更加流行的，但是后来发现，max pooling更更有效地提取feature map的特征，因此在近些年的网络架构中，max pooling变得更加流行。）

average pooling更强调对整体特征信息进行下采样，在全局平均池化中应用较广。

问题2：我们现在已经知道的BP算法基本上都是针对全连接神经网络的BP算法（诸如链式法则之类的），那么，在CNN中各层又是如何BP的（尤其是卷积层和池化层）？

答：参考：https://becominghuman.ai/back-propagation-in-convolutional-neural-networks-intuition-and-code-714ef1c38199

以及：https://stats.stackexchange.com/questions/326377/backpropagation-on-a-convolutional-layer

以及：https://lanstonchu.wordpress.com/2018/09/01/convolutional-neural-network-cnn-backward-propagation-of-the-pooling-layers/

卷积层的BP是靠反向传播过来的梯度在原始图像上滑动、卷积形成的！

因此，卷积层的BP依旧是一个卷积！正如图2所示：

2.PNG

假设损失函数用表示，当我们想求解时，可以借助以下方法求解：
$\frac{\partial L}{\partial W_{11}} = \frac{\partial L}{\partial h_{11}} \frac{\partial h_{11}}{\partial W_{11}} + \frac{\partial L}{\partial h_{12}} \frac{\partial h_{12}}{\partial W_{11}} + \frac{\partial L}{\partial h_{21}} \frac{\partial h_{21}}{\partial W_{11}} + \frac{\partial L}{\partial h_{22}} \frac{\partial h_{22}}{\partial W_{11}}$

$\frac{\partial L}{\partial W_{12}} = \frac{\partial L}{\partial h_{11}} \frac{\partial h_{11}}{\partial W_{12}} + \frac{\partial L}{\partial h_{12}} \frac{\partial h_{12}}{\partial W_{12}} + \frac{\partial L}{\partial h_{21}} \frac{\partial h_{21}}{\partial W_{12}} + \frac{\partial L}{\partial h_{22}} \frac{\partial h_{22}}{\partial W_{12}}$

$\frac{\partial L}{\partial W_{21}} = \frac{\partial L}{\partial h_{11}} \frac{\partial h_{11}}{\partial W_{21}} + \frac{\partial L}{\partial h_{12}} \frac{\partial h_{12}}{\partial W_{21}} + \frac{\partial L}{\partial h_{21}} \frac{\partial h_{21}}{\partial W_{21}} + \frac{\partial L}{\partial h_{22}} \frac{\partial h_{22}}{\partial W_{21}}$

$\frac{\partial L}{\partial W_{22}} = \frac{\partial L}{\partial h_{11}} \frac{\partial h_{11}}{\partial W_{22}} + \frac{\partial L}{\partial h_{12}} \frac{\partial h_{12}}{\partial W_{22}} + \frac{\partial L}{\partial h_{21}} \frac{\partial h_{21}}{\partial W_{22}} + \frac{\partial L}{\partial h_{22}} \frac{\partial h_{22}}{\partial W_{22}}$

注意到：

记
$\frac{\partial L}{\partial h} = \left [ \begin{matrix} \frac{\partial L}{\partial h_{11}} & \frac{\partial L}{\partial h_{12}} \\ \frac{\partial L}{\partial h_{21}} & \frac{\partial L}{\partial h_{22}} \end{matrix} \right ]$
则式（5）~（8）可以用矩阵表示为：

其中的“*”号表示的是卷积运算（和正向传播中的卷积操作是一样的）。如果我们现在把看做是反向传播过程中的卷积核，那么仔细观察式（11）~（14），我们便会发现：这几个式子实际上就是这个偏导数卷积核在3 x 3的输入矩阵上做卷积的结果！卷积核向右和向下滑动的步长均为1，而且没有padding。因此可以说：卷积层的反向传播依旧是卷积！

那么在池化层中，梯度又该如何反向传播呢？

在max pooling中，正向传播时，仅仅是将某个区域（以2 x 2区域为例）的最大值保留了下来，其他值舍去。因此max pooling层在反向传播时有如下特点：

只有输入图像中在这个2 x 2区域内取得最大值的位置才会有梯度传播过去，此时，池化层本身提供的梯度值是1，这个1将会和其他传递过来的梯度相乘，作为最终池化层在这个最大值位置上的梯度（其实就是传递了一下，并没有改变原梯度的值，因为pooling层本身并没有做任何学习，它们只是负责减小输入特征的维度从而减少网络的参数以减轻计算负担，因此梯度到它们这里只是简单地传递了一下）；
在输入图像中这个2 x 2区域最大值以外的其他位置上，没有梯度会传播过去，因此这些位置的梯度都将被置零。

在average pooling中，正向传播时，每一个point都会对输出产生影响，那么这种影响在反向传播时是如何传递回去的呢？

如图3所示：

3.PNG

左图的5 x 5网格经average pooling后变成右边的3 x 3网格，其中黄颜色的格子在对右边的每一个网格都有贡献，而且均贡献了的作用。那么在反向传播时，黄颜色格子的梯度就将由9份组成：右边3 x 3网格中每个格子都将为其提供的梯度。假设右边网格中现在的数字是已经传播过来的梯度的数值，那么经反向传播后，原始feature map（即左边5 x 5的网格）中黄颜色格子最终的梯度值为：
$\frac{\partial L}{\partial X_{33}} = \frac{1}{9} \times 1 + \frac{1}{9} \times 3 +\frac{1}{9} \times 1 +\frac{1}{9} \times 1 +\frac{1}{9} \times 4 +\frac{1}{9} \times 2 +\frac{1}{9} \times 6 +\frac{1}{9} \times 2 +\frac{1}{9} \times 1 = \frac{21}{9}$
对于其他的格子，都是根据这种方法计算反向传播的梯度值的，关键是要找出原始feature map中每个格子到底对pooling后的结果做出了多少贡献，然后依据这个贡献度来计算反向传播的梯度。

问题3：Batch Normalization层（简称bn层）是CNN中的一个特殊的层，那么BP算法在bn层又是如何传播的？

以下主要参考：https://kratzert.github.io/2016/02/12/understanding-the-gradient-flow-through-the-batch-normalization-layer.html

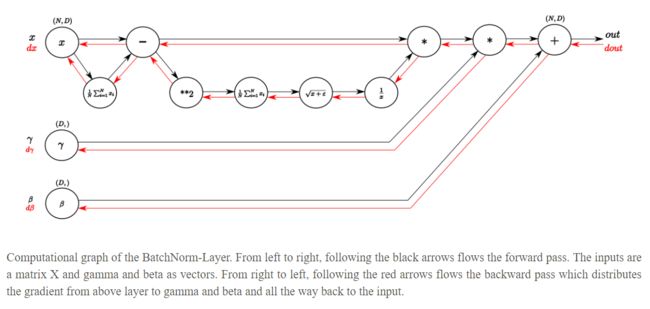
答：Batch Normalization层的正向传播如图5所示：

5.PNG

按照黑色的箭头从左到右一共可以分成9步：

假设一个mini-batch中有N个数据，则：

step 1：计算一个mini-batch中的平均值：
step 2：用原始的x减去这个平均值：
step 3：计算：，这是为了计算方差用的；
step 4：计算方差：
step 5：计算标准差：

这里之所以要加上，是因为这个标准差是出现在分母位置上的，必须要保证分母的值总是有意义的（如不能为0）；
step 6：取标准差的倒数：
step 7：将求得的x的平均值和标准差的导数乘起来：
step 8：然后再乘以系数：
step 9：最后再加上：

那么，在反向传播的时候，我们就可以根据这9步，从后往前一步一步地推导梯度的传播。假设从后面的网络中传过来的梯度是（如图5中红色箭头的起点所示），即：

则：

首先根据step 9：

则关于参数的梯度为：

注意到，这个式子计算出的只是1个sample的梯度，而batch normalization每次是针对一个mini-batch来进行的，因此我们需要把每一个sample关于的梯度加起来，从而得到这一个mini-batch关于的梯度（假设这个mini-batch中有N个样本）：

这样，关于参数的梯度就表示出来了。
然后根据step 8，关于参数的梯度也可以表示出来：

这里需要注意的依然是要把整个mini-batch中所有样本关于的梯度加起来，得到的才是最终的梯度值。
根据step 7，可以将关于x的平均值和x标准差的倒数的梯度表示出来：

$\frac{\partial L}{\partial {\frac{1}{\sqrt{\sigma^2 + \epsilon}}}} = \frac{\partial L}{\partial \hat x} \frac{\partial \hat x}{\partial {\frac{1}{\sqrt{\sigma^2 + \epsilon}}}} = \gamma \cdot \sum\limits_{i=1}^N dout \cdot \bar x$

其中用到的和分别在step 2和step 6中已经计算出。
根据step 6，可以计算出关于标准差的梯度：
$$
\begin{equation}
\begin{aligned}
\frac{\partial L}{\partial \sqrt{\sigma^2 + \epsilon}} =

\frac{\partial L}{\partial {\frac{1}{\sqrt{\sigma^2 + \epsilon}}}} \frac{\partial {\frac{1}{\sqrt{\sigma^2 + \epsilon}}}}{\partial \sqrt{\sigma^2 + \epsilon}}
&= \gamma \cdot \sum\limits_{i=1}^N dout \cdot \bar x \cdot [- \frac{1}{(\sqrt{\sigma^2 + \epsilon})^2}] \
&= \gamma \cdot \sum\limits_{i=1}^N dout \cdot \bar x \cdot (- \frac{1}{\sigma^2 + \epsilon})
\end{aligned}
\end{equation}
$$
其中用到的在step 4中已经计算出来了。
根据step 5，可以计算出关于的梯度：
$\frac{\partial L}{\partial \sigma^2} = \frac{\partial L}{\partial \sqrt{\sigma^2 + \epsilon}} \frac{\partial \sqrt{\sigma^2 + \epsilon}}{\partial \sigma^2} = \gamma \cdot \sum\limits_{i=1}^N dout \cdot \bar x \cdot (- \frac{1}{\sigma^2 + \epsilon}) \cdot \frac{1}{2\sqrt{\sigma^2 + \epsilon}}$
根据step 4，可以求出关于的梯度，求和操作引入的梯度累乘因子是1：
$\frac{\partial L}{\partial \bar x^2} = \frac{\partial L}{\partial \sigma^2} \frac{\partial \sigma^2}{\partial \bar x^2} = \frac{1}{N} \sum\limits_{i=1}^N \gamma \cdot \sum\limits_{i=1}^N dout \cdot \bar x \cdot (- \frac{1}{\sigma^2 + \epsilon}) \cdot \frac{1}{2\sqrt{\sigma^2 + \epsilon}}$
根据step 3，可以求得关于的梯度：
$\begin{equation} \begin{aligned} \frac{\partial L}{\partial \bar x } = \frac{\partial L}{\partial \bar x^2} \frac{\partial \bar x^2}{\partial \bar x} &= \frac{1}{N} \sum\limits_{i=1}^N \gamma \cdot \sum\limits_{i=1}^N dout \cdot \bar x \cdot (- \frac{1}{\sigma^2 + \epsilon}) \cdot \frac{1}{2\sqrt{\sigma^2 + \epsilon}} \cdot 2 \bar x \\ &= \frac{1}{N} \sum\limits_{i=1}^N \gamma \cdot \sum\limits_{i=1}^N dout \cdot \bar x^2 \cdot (- \frac{1}{\sigma^2 + \epsilon}) \cdot \frac{1}{\sqrt{\sigma^2 + \epsilon}} \end{aligned} \end{equation}$
现在到了step 2，注意这样一个规定：

在反向传播和计算图的定义中，当两个梯度沿着两条不同的路径汇聚到一个节点时，此时这个节点的梯度将等于这两个梯度之和。

根据图5可知，传播到这个节点的梯度是由两条路径上的梯度组成的：一条来自step 3中关于的梯度，另一条来自step 7中关于的梯度。因此，关于的梯度为：
$\begin{equation} \begin{aligned} \frac{\partial L}{\partial x} &= 1 \cdot ( \frac{\partial L}{\partial \bar x}|_{\text{来自step 3}} + \frac{\partial L}{\partial \bar x}|_{\text{来自step 7}}) \\ &= \frac{1}{N} \sum\limits_{i=1}^N \gamma \cdot \sum\limits_{i=1}^N dout \cdot \bar x^2 \cdot (- \frac{1}{\sigma^2 + \epsilon}) \cdot \frac{1}{\sqrt{\sigma^2 + \epsilon}} + \gamma \cdot \sum \limits _{i=1}^N dout \cdot \frac {1}{\sqrt{\sigma^2 + \epsilon}} \end{aligned} \end{equation}$

关于的梯度为：
$\begin{equation} \begin{aligned} \frac{\partial L}{\partial{\frac{1}{k} \sum _{i=1}^N x_i }} &= -1 \cdot ( \frac{\partial L}{\partial \bar x}|_{\text{来自step 3}} + \frac{\partial L}{\partial \bar x}|_{\text{来自step 7}}) \\ &= - \left[ \frac{1}{N} \sum\limits_{i=1}^N \gamma \cdot \sum\limits_{i=1}^N dout \cdot \bar x^2 \cdot (- \frac{1}{\sigma^2 + \epsilon}) \cdot \frac{1}{\sqrt{\sigma^2 + \epsilon}} + \gamma \cdot \sum \limits _{i=1}^N dout \cdot \frac {1}{\sqrt{\sigma^2 + \epsilon}} \right] \end{aligned} \end{equation}$

现在到step 1了，这一步类似于step 4，依据step 2中求得的关于的梯度，可以求出由传递过来的关于的梯度：
$\begin{equation} \begin{aligned} \frac{\partial L}{\partial x} &=\frac{\partial L}{\partial{\frac{1}{k} \sum _{i=1}^N x_i }} \frac{\partial{\frac{1}{k} \sum _{i=1}^N x_i }}{\partial x} \\ &= - \frac{1}{N} \sum\limits_{i=1}^N \left[ \frac{1}{N} \sum\limits_{i=1}^N \gamma \cdot \sum\limits_{i=1}^N dout \cdot \bar x^2 \cdot (- \frac{1}{\sigma^2 + \epsilon}) \cdot \frac{1}{\sqrt{\sigma^2 + \epsilon}} + \gamma \cdot \sum \limits _{i=1}^N dout \cdot \frac {1}{\sqrt{\sigma^2 + \epsilon}} \right] \end{aligned} \end{equation}$
整个梯度推导结束了吗？没有，还差最后一步！注意到最终反向传播到的梯度是由两条路径汇聚而成的，因此要将这两条路径的梯度相加，才能最终得到关于的梯度：
$\begin{equation} \begin{aligned} \frac{\partial L}{\partial x} &= \frac{\partial L}{\partial \bar x}|_{\text{来自step 2}} + \frac{\partial L}{\partial \bar x}|_{\text{来自step 1}} \\ &= \left[ \frac{1}{N} \sum\limits_{i=1}^N \gamma \cdot \sum\limits_{i=1}^N dout \cdot \bar x^2 \cdot (- \frac{1}{\sigma^2 + \epsilon}) \cdot \frac{1}{\sqrt{\sigma^2 + \epsilon}} + \gamma \cdot \sum \limits _{i=1}^N dout \cdot \frac {1}{\sqrt{\sigma^2 + \epsilon}} \right ] - \\ & \frac{1}{N} \sum\limits_{i=1}^N \left[ \frac{1}{N} \sum\limits_{i=1}^N \gamma \cdot \sum\limits_{i=1}^N dout \cdot \bar x^2 \cdot (- \frac{1}{\sigma^2 + \epsilon}) \cdot \frac{1}{\sqrt{\sigma^2 + \epsilon}} + \gamma \cdot \sum \limits _{i=1}^N dout \cdot \frac {1}{\sqrt{\sigma^2 + \epsilon}} \right] \end{aligned} \end{equation}$
至此，我们便完成了Batch Normalization层在反向传播中所有参数梯度的推导。

激活层

关于各种激活函数的用法以及各种tricks主要参考：http://lamda.nju.edu.cn/weixs/project/CNNTricks/CNNTricks.html（由于内容太多，本文只总结了部分内容）

Sigmoid函数：指的是一类特殊的logistic function，它能够产生之间的概率化输出（能够将输入压缩到[0,1]之间），曲线的形状类似于“S”，函数表达式如下：

Sigmoid函数广泛用于二分类。

tanh函数：是Sigmoid函数的一个替代函数，形状和Sigmoid函数类似，也是“S”型，区别是tanh函数的值域是。因此对tanh函数而言，负的输入将会被映射成负的输出。tanh函数的表达式如下：

tanh函数是关于原点中心对称的。

Softmax函数：计算每一个目标种类的概率分布，常用于多分类任务。表达式如下：

ReLU函数：当输入小于0时，输出为0；当输入大于0时，输出和输入相同。表达式如下：

Leaky ReLU：当输入大于0时，和ReLU函数相同；当输入小于0时，不再将输出置零，而是用一个比较小的数和输入相乘来作为输出，表达式如下：

LeakyReLU主要是为了解决“dying ReLU”的问题（"dying ReLU": the ReLU activation function always outputs the same value (zero) for any input）。

Parametric ReLU（PReLU）：与Leaky ReLU相比，PReLU在负半平面的斜率不再是预先定义的常数，而是从数据中学得的。

Randomized ReLU（RReLU）：在RReLU中，负半平面的斜率是按以下方式给定的：

在训练过程中，是在一个给定的范围内随机选取的；
在测试过程中，是确定的。

这三种ReLU函数的图像如图1_1_1所示：

1_1_1.PNG

使用激活函数的目的是为了引入非线性，否则即使神经网络有再多的层，将所有的这些层加起来后，最终得到的仍然只是一个线性函数，和单层感知机无异。

哪一个激活函数是最好的？

答案是没有哪一个激活函数永远是最好的，这取决于要解决的具体问题：

（1）对于二分类任务，可以采用Sigmoid函数或tanh函数；

（2）对于多分类任务，可以采用Softmax函数；

（3）对于多层的神经网络，隐层最好使用ReLU函数，因为Sigmoid函数和tanh函数两端存在饱和区，在这一区域梯度为0，这就导致网络在反向传播的过程中可能会出现梯度消失的现象，当网络非常深时，梯度将很难传播到前面的层。而且Sigmoid函数和tanh函数都涉及到指数运算，运算代价昂贵，而ReLU函数运算简单，计算代价小。且ReLU函数不存在饱和区，不会出现梯度消失的现象。

但ReLU函数也有一个缺点：当输入小于0时，ReLU函数的输出为0，而此时的梯度也为0，此时就会陷入“dying ReLU”的问题，而且很难从这一状态中恢复出来。

而Leaky ReLU、PReLU、RReLU可以解决这个问题，当输入小于0时，Leaky ReLU不再恒定地输出0，而是输出(是一个小常数，e. g. )。

全连接层

在全连接层中，我们将最后一个卷积层的输出展平，并将当前层的每个节点和下一层的另一个节点连接起来（就相当于普通ANN中的全连接层）。全连接层相当于对我们之前的所有操作进行一个总结，给我们一个最终的结果。

其他重要的知识

CNN真正能做的，只是起到一个特征提取器的作用。

卷积核也被称为feature，原始图片经过卷积核的卷积运算后，得到的矩阵称为feature map。feature map是每一个feature从原始图像中提取出来的“特征”，一个feature作用于图片，产生一张feature map。

所谓神经网络的“训练”，其实训练的就是卷积核里面的参数，训练的依据就是BP算法，训练的目标是使误差函数不断下降，训练方法是梯度下降法。

图像的上采样与下采样

下采样：下采样是对图像进行缩小。

对于一幅图像I尺寸为M*N，对其进行s倍下采样，即得到(M/s)*(N/s)尺寸的分辨率图像。如果考虑的是矩阵形式的图像，就是把原始图像s*s窗口内的图像变成一个像素。

上采样：上采样的主要目的是放大图像，提高图像的分辨率。上采样主要有以下三种方式：

参考：https://blog.csdn.net/u014451076/article/details/79156967

（1）双线性插值（bilinear）：在语义分割中用的较多，这种方法的特点是不需要进行学习，运行速度快，操作简单。

（2）反卷积（Deconvolution，又叫转置卷积）：它和卷积做相反的运算，可以还原图片的原始尺寸。

如果卷积运算可表示为：

其中x是输入矩阵，y是输出矩阵，C是关于卷积核的权重矩阵。则反卷积可表示为：

同理，在反向传播时，卷积的反向传播可表示为：

而在反向传播时，反卷积的反向传播可表示为：

反卷积就相当于不再乘以原始的权重矩阵，而是乘以原始权重矩阵的转置矩阵。

参考：https://www.zhihu.com/question/43609045?sort=created

问题1：反卷积的具体实现是什么样的？

答：如图6所示。

6.PNG

图中下方的蓝色方块是feature map，其中的灰色3 x 3矩阵就是转置过的卷积核，上方墨绿色的5 x 5矩阵就是反卷积后恢复出来的图像。在实际的操作过程中，被用来进行反卷积的feature map 通常都是以图6所示的方式来填充padding的——在feature map的行、列之间以相同的数目嵌入padding（嵌入效果如图6所示，嵌入之后feature map中的每个小格子将被padding隔开），而不是像卷积过程一样只在原始图像的四周填充padding。

（3）反池化（unpooling）：在池化过程中，记录下max-pooling在对应kernel中的坐标，在反池化过程中，将一个元素根据kernel进行放大，根据之前的坐标将元素填写进去，其他位置补0.

反卷积的用途：（参考：https://blog.csdn.net/g11d111/article/details/82350563）

FCN（U-net）中low-level与high-level特征的融合：

网络比较深的时候，feature map通常比较小，对这种feature map进行上采样有很好的语义信息，但分辨率很差；
网络比较浅的时候，feature map通常比较大（接近input image），对这种feature map进行上采样有很好的细节，但语义信息很差。

反卷积的示意图：https://blog.csdn.net/g11d111/article/details/82350563

反卷积和反池化的示意图：https://blog.csdn.net/A_a_ron/article/details/79181108

Batch Normalization：（参考：https://www.cnblogs.com/guoyaohua/p/8724433.html）

以下总结博客中的基本要点：

机器学习假设训练数据和测试数据是满足相同分布的，这是通过训练数据获得的模型能够在测试集获得好的效果的基本保障。而Batch Normalization就是在深度神经网络训练过程中使得每一层神经网络的输入保持相同的分布的。
Batch Normalization是基于Mini-batch SGD的，Mini-batch SGD相对于One-example SGD有两个突出的优势：

（i）梯度更新方向更准确；

（ii）并行计算速度更快。

而且SGD训练的过程中超参数调节起来很麻烦。
Internal Covariate Shift：

对于深度学习这种包含很多隐层的网络结构，在训练过程中，因为各层参数在不停地变化，所以每个隐层都会面临covariate shift的问题，也就是在训练过程中，隐层的输入分布老是变来变去，这就是所谓的“Internal Covariate Shift”。其中的Internal指的是深层网络的隐层，是发生在网络内部的事情。

而Batch Normalization就是想让每个隐层节点的输入分布固定下来。
Batch Normalization的核心思想：

深层神经网络在做非线性变换前的激活输入值（就是那个，是输入）随着网络深度加深或者在训练过程中，其分布逐渐发生偏移或者变动，之所以训练收敛慢，一般是整体分布逐渐往非线性函数的取值区间的上下限两端靠近（对于Sigmoid函数来说，意味着激活输入值是大的负值或正值），所以这导致反向传播时低层神经网络的梯度消失，这是训练深层神经网络收敛越来越慢的本质原因。而Batch Normalization就是通过一定的规范化手段，把每层神经网络任意神经元这个输入值的分布强行拉回到均值为0方差为1的标准正态分布，其实就是把越来越偏的分布强制拉回比较标准的分布，这样使得激活输入值落在非线性函数对输入比较敏感的区域，这样输入的小变化就会导致损失函数较大的变化，亦即让梯度变大，避免梯度消失问题产生，而且梯度变大意味着学习收敛速度快，能大大加快训练速度。

这一过程用公式表示如下：

注意，这个公式表示的是某个神经元对应的原始的激活x通过减去mini-batch内m个实例获得的m个激活函数求得的均值E(x)并除以求得的方差Var(x)来得到规范化后的激活。
Batch Normalization中的scale和shift操作：

经过BN后，大部分Activation的值落入非线性函数（如Sigmoid函数）的线性区内，其对应的导数远离饱和区，通过这种方法来加速训练的收敛过程。

但是，如果都通过BN，那不就跟把非线性函数替换成线性函数效果相同了？即网络就好像是多层的线性函数一样，而这就意味着网络的表达能力下降了，也意味着“深度”的意义就没有了。所以BN为了保证非线性的获得，对变换后的满足均值为0方差为1的x又进行了scale加上shift操作（y = scale * x + shift），每个神经元增加了两个参数scale和shift参数，这两个参数是通过训练学习到的。这一操作就等价于非线性函数的值从正中心周围的线性区往非线性区动了动。其核心思想可能是想找到一个线性和非线性的较好平衡点，既能享受非线性的较强表达能力的好处，又能避免太靠近非线性区两头使得网络收敛速度太慢。

这一过程用论文中的公式表示如下：
论文中，Batch Normalization的整体操作流程如图4所示：

4.PNG

卷积神经网络中重要的基础知识汇总

输入层

卷积层

池化层

激活层

全连接层

其他重要的知识

你可能感兴趣的:(卷积神经网络中重要的基础知识汇总)