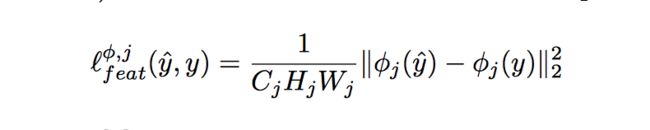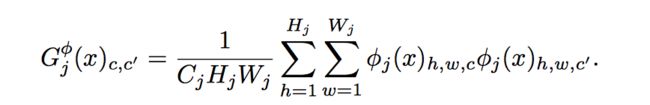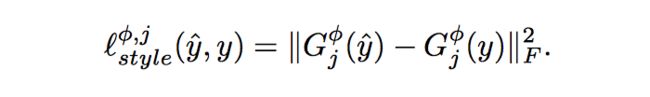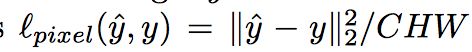本文是基于Perceptual Losses for Real-Time Style Transfer and Super-Resolution这篇论文的总结。原文链接:https://arxiv.org/pdf/1603.08155.pdf 。
一.摘要:
该方法适用于图像转换的问题,即一张输入图片被转为输出图片。
当前用于解决该问题的方法有两种:
1. 使用基于单像素点损失函数(输出和标准图片的损失)的前馈卷积神经网络。
2. 通过定义及优化感知损失函数,其是基于从预训练的网络中提取的高质量特征。
而此文,是将两种方法的优点结合起来,提出了一种能利用感知损失函数来训练的前馈神经网络。
二.简介:
很多经典的问题都可以看作是图像转换的问题。比如是图像处理问题(去噪,高分辨率和染色法),在这些问题中,输入的图片都是很低级的(含噪声,低分辨率和灰度级),但输出都是高质量的彩色图片。再比如,在计算机视觉领域的语义分割(语义分割好文:http://www.tuicool.com/articles/eEfm2mv)和深度预测,即输入是一张彩色的图片,而输出是一张将场景的语义或者地理信息编码了的图片。
解决这个问题的一种方法是用监督学习的方法,训练一个前馈卷积神经网络,基于单像素点的损失函数去衡量输出和标准图片的差距。这个方法被广泛使用,比如:
1. Dong, C., Loy, C.C., He, K., Tang, X.: Image super-resolution using deep convolutional networks. (2015)
2. Cheng, Z., Yang, Q., Sheng, B.: Deep colorization. In: Proceedings of the IEEE
International Conference on Computer Vision. (2015) 415–423
3. Long, J., Shelhamer, E., Darrell, T.: Fully convolutional networks for semantic
segmentation. CVPR (2015)
但是,这个单像素点误差的方法不能捕捉输出和标准图片的感知差别。比如,两幅完全相同的照片,但是有1个像素点的偏移。尽管在感知上是相似的(即你察觉不出来一个像素点的偏移对成像有什么影响),但是在单像素点误差的方法上衡量却是有极大的差别。
同时,最近的工作表明,高质量的图片能够通过感知损失函数得来,但不是基于单像素点误差的方法,而是基于与预先训练的卷积神经网络从提取出的高水平图片特征的不同。
我们的方法是结合了这两种方法,使得其更具有鲁棒性。
该方法在两种任务中做了实验:风格迁移和单图像高分辨率。
三.相关工作:
1.前馈图像转换
2.感知优化
3.风格迁移:将一张图片的内容同另外一张图片的风格结合起来。这个是基于风格重建损失函数。
4.图像超分辨率
四.方法
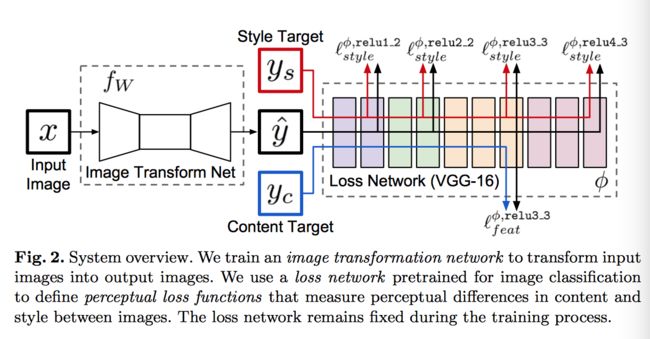
如上图所示,该系统由两部分组成:图像转换网络fw和损失网络(用来定义许多的损失函数)。图像转换网络是一个通过权重W表示的深度残差卷机神经网络;他通过一个映射y=fw(x)将输入图片x转换为输出图片y。每个损失函数计算了一个标量值,其衡量了输出图片与标准图片的差距。这个网络用随机梯度下降的方法去优化损失函数。
为了解决单像素点损失的缺点,使我们的损失函数更好的衡量图片间的感知和语义差别,我们从最近的论文中得到了些灵感。这些方法的核心思想就是预先训练的图像分类的卷机神经网络能够学习到如何将我们将要在损失函数进行衡量的感知和语义信息进行编码。
损失网络是用来定义特征重建损失和风格重建损失。对于每个输入图片,我们都有一个内容目标和风格目标。对于风格迁移,内容目标是输入图片x,输出图片是内容目标和风格目标的结合,我们为每个风格目标训练一个网络。对于单图片超分辨率,输入是低分辨率的图片,内容目标是标准高分标率突破,风格重建损失没有用到。
1. 图像转换网络
这个网络中,我们没有使用pooling layer,而是使用strided and fractionally strided convolutions for in-network downsampling and upsampling.我们的网络借助了其他论文的结构,使用了五个残差块。所有的非残差卷基层都是用了batch normalization和Relu的非线性输出层。除了第一层和最后一层用了9*9的卷积核,所有的卷积层都是用了3*3的卷积核。
输入输出:
风格迁移的输入输出都是3*256*256的彩色图片。超分辨率的规格是unsampling因子f,输出是3*288*288的高分辨率图片,输入是3*288/f*288/f低分辨率图片。因为图片转换网络是全卷积的,所以对于任何的分辨率都可以用。
上采样与下采样:
downsampling即下采样,主要是对数字信号进行下采样操作,例如数字图像处理中对图片进行压缩时,N*N的矩阵变成了(N/2)*(N/2),这个步骤就是对原图片进行了下采样。还有一个例子,在离散小波变换(DWT)中,每次将m层的低频成分的系数(n个)通过低通滤波器以后得到m-1层的n个低频成分系数,通过高通滤波器以后得到m-1层的n个高频成分系数,如果直接合并就成了2n个系数,这里需要对两种成分各自进行下采样,使得经过变化后的系数依然保持n个。
upsampling与downsampling概念相反,也可以理解成插值(interpolation)。举个例子,比如在放大某个数字图像的时候,新放大的图像的某些像素点的值是需要预测插值的,这个插值的过程其实就是上采样。
取自:https://www.zhihu.com/question/19913939/answer/13685695
对于超分辨率,上采样因子f,在步长为1/2,log2f层卷积层后用了几个残差块。这个与用双三次插值低像素图片后再输入到网络的方法不同。比起依赖于用一个固定的上采样方程,fractionally-strided的卷积使得上采样方程能够从剩下的网络中学习到。
补一个:双三次插值:http://blog.csdn.net/qq_29058565/article/details/52769497
对于风格迁移,我们网络使用步长为2的卷积网络和几个残差块去做下采样,然后再用步长为1/2的两个卷基层去做上采样。尽管输入和输出有着相同的大小,先做下采样然后再上采样有几个好处。
1. 计算量。 如果是最简单的方法,对C*H*W的输入区域用3*3的卷积和滤波器C,需要9hwc^2的乘加,这个的代价和在DC*H/D*W/D的输入上用3*3的卷积用DC滤波器的代价是一样的。在下采样之后,我们可以在相同的代价上用一个更大的网络。
2. 有效的感受野大小。高质量的风格迁移需要连贯的改变原图片的大部分区域,所以对于在输出的每个像素点如果有一个大的有效的局部感受野的话,无疑是有巨大的好处。如果没有下采样的话,每个3*3的卷积层增加了2个单位的局部感受野。但是在D因子的下采样之后,每个3*3的卷积层增加了2D大小的局部感受野,那就是说在相同数量的卷积层上,能够有更大的局部感受野。
残差连接:
用了许多residual blocks,每个block包含了2层3*3的卷积层。
2. 感知损失函数
Feature Reconstruction Loss:
比起直接的计算每个输出的像素点与标准图片的像素点的差距,我们计算由pre-trained的损失网络计算出来的相似特征表达的差距。公式如下:
Style Reconstruction Loss:
feature reconstruction loss惩罚了输出图片当其与目标图片偏离。我们同样惩罚图片在风格上,比如颜色,质地和模式等。为了达到这个效果,提出了style reconstruction loss。公式如下:
3. 简单的损失函数
除了上面定义的感知损失函数,我们也定义了两个简单的仅依赖于低级的像素信息的损失函数。
Pixel Loss:
这个loss是输出图片与标准图片的像素的欧式距离。如果它们都是C*H*W的大小,那么像素loss可以定义为:
Total Variation Regularization
五. 实验
1. 风格迁移
2. 单图片的超分辨率
对于单图片的超分辨率,这个任务是从低分辨率的输入去生成一个高分辨率的输出。这歌问题很棘手,因为对于每个低分辨率的图片来说,都存在着生成多个高分辨率的图片的可能性。这个问题随着扩大因子的变大而变得越来越棘手,因为很难从低像素的图片中找到支持高分辨率细节的证据。为了克服这个困难,我们用图像特征重建函数来代替简单的像素损失函数。
补充:
超分辨率:指的是将低像素的图片转化为高像素的图片。图片的分辨率高还是低取决于像素点的个数。如果要得到高的分辨率,那么图片的大小必定要发生改变。这里的输入是将原图进行下采样,然后喂进神经网络,然后输出同原图一样的大小。所以和输入对比的话,输出的大小是变化了的。
The usual way of training a network:
You want to train a neural network to perform a task (e.g. classification) on a data set (e.g. a set of images). You start training by initializing the weights randomly. As soon as your start training, the weights are changed in order to perform the task with less mistakes (i.e. optimization). Once you're satisfied with the training results you save the weights of your network somewhere.
You are now interested in training a network to do perform a new task (e.g. object detection) on a different data set (e.g. images too but not the same as the ones you used before). Instead of repeating what you did for the first network and start from training with randomly initialized weights, you can use the weights you saved from the previous network as the initial weight values for your new experiment. Initializing the weights this way is referred to as using a pre-trained network. The first network is your pre-trained network. The second one is the network you are fine-tuning.
The idea behind pre-training is that random initialization is...well...random, the values of the weights have nothing to do with the task your trying to solve. Why should a set of values be any better than another set? But how else would you initialize the weights? If you knew how to initialize them properly for the task, you might as well set them to the optimal values (slightly exaggerated). No need to train anything. You have the optimal solution to your problem. Pre-training gives the network a head start. As if it has seen the data before.
What to watch out for when pre-training:
The first task used in pre-training the network can be the same as the fine-tuning stage. The datasets used for pre-training vs. fine-tuning can also be the same, but can also be different. It's really interesting to see how pre-training on a different task and different dataset can still betransferredto a new dataset and new task that areslightlydifferent. Using a pre-trained network generally makes sense if the both tasks or both datasets have something in common. The bigger the gap, the less effectvie pre-training will be. It makes little sense to pre-train a network for image classification by training it one financial data first. In this case there's too muchdisconnectbetween the pre-training and fine-tuning stages.